Độ dài bóng đen tạo thành trên đáy bể là:
Ta có: \(\dfrac{{{\rm{Sin i}}}}{{{\rm{Sin r}}}} = {\rm{n = }}\dfrac{4}{3} = > {\mathop{\rm sinr}\nolimits} = \dfrac{3}{4}.\sin i\)
Mà \(i = {90^0} - {30^0} = {60^0}\)=> \({\mathop{\rm sinr}\nolimits} = \dfrac{3}{4}.\sin i = \dfrac{3}{4}.\sin {60^0} = \dfrac{{3\sqrt 3 }}{8} = > r = {40,51^0}\)
Xét tam giác vuông ICD có \(CD = IC.\tan r = BH.\tan r = 60.\tan r = 60.\tan {40,51^0} = 51,25\)
=> Độ dài bóng đen tạo thành trên đáy bể là HD= HC + CD = BI + CD = 34,6 + 51,25 = 85,85 cm
Độ dài bóng đen tạo thành trên mặt nước là:
- Ta có: AB = AH – BH = 80 – 60 = 20 cm
- Xét tam giác vuông ABI có: \(\tan {30^0} = \dfrac{{AB}}{{BI}} \to BI = \dfrac{{AB}}{{\tan {{30}^0}}} = \dfrac{{20}}{{\tan {{30}^0}}} = 34,6\)
=> độ dài bóng đen tạo thành trên mặt nước là \(BI = 34,6\)
Độ dài bóng đen tạo thành trên mặt nước là:
- Ta có: AB = AH – BH = 80 – 60 = 20 cm
- Xét tam giác vuông ABI có: \(\tan {30^0} = \dfrac{{AB}}{{BI}} \to BI = \dfrac{{AB}}{{\tan {{30}^0}}} = \dfrac{{20}}{{\tan {{30}^0}}} = 34,6\)
=> độ dài bóng đen tạo thành trên mặt nước là \(BI = 34,6\)
Khoảng cách giữa tia tới và tia ló là:
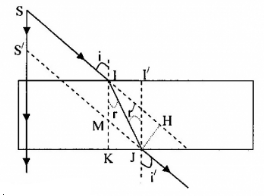
- Gọi d là khoảng cách giữa giá của tia tới và tia ló, d = JH
- Xét tam giác vuông IJH: \(JH = {\rm{IJ}}.\sin (i - r)\)
- Xét tam giác vuông IJK: \({\rm{IJ = }}\dfrac{{IK}}{{{\mathop{\rm cosr}\nolimits} }} = \dfrac{e}{{\cos r}}\)
=> \(d = JH = \dfrac{e}{{c{\rm{osr}}}}.\sin (i - r)\)
- Tính r:
Áp dụng định luật khúc xạ ánh sáng có: \(\sin i = n.\sin r \to \sin {45^0} = 1,5.sin{\rm{r}} \to r = {28,13^0}\)
- Thay số tính d: với e = 10 cm
=> \(d = JH = \dfrac{{10}}{{c{\rm{os(28}}{\rm{,13)}}}}.\sin (45 - 28,13) = 3,29cm\)
Khi đó tia ló khỏi bản sẽ:
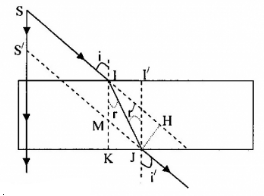
- Vẽ đường truyền của tia sáng SI qua bản mặt song song như hình vẽ
- Tia tới SI tới mặt thứ nhất của bản mặt song song:
+ Góc tới i; thu được tia khúc xạ IJ: góc khúc xạ r
- Tia tới IJ tới mặt thứ hai của bản mặt song song:
+ Góc tới r’; thu được tia ló Jx: góc khúc xạ i'
Vì r = r’ => i = i'
=> tia ló song song với tia tới
Khi đó tia ló khỏi bản sẽ:

- Vẽ đường truyền của tia sáng SI qua bản mặt song song như hình vẽ
- Tia tới SI tới mặt thứ nhất của bản mặt song song:
+ Góc tới i; thu được tia khúc xạ IJ: góc khúc xạ r
- Tia tới IJ tới mặt thứ hai của bản mặt song song:
+ Góc tới r’; thu được tia ló Jx: góc khúc xạ i'
Vì r = r’ => i = i'
=> tia ló song song với tia tới
Ảnh \(S'\) của \(S\) qua bản hai mặt song song cách bản hai mặt song song một khoảng:
- Khoảng cách từ S tới bản mặt song song: 20 cm
- Khoảng cách SS’ từ câu a: 2 cm
=> Khoảng cách từ S’ tới bản mặt song song: 20 – 2 = 18 cm
Ảnh \(S'\) của \(S\) qua bản hai mặt song song cách \(S\) một khoảng:
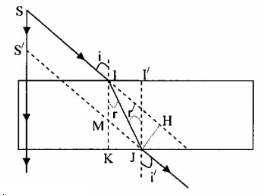
- Độ dời ảnh: SS’ = IM = IK – MK = e – MK
- Xét tam giác vuông MKJ: \(MK = \dfrac{{KJ}}{{\tan i}} = \dfrac{{II'}}{{\tan i}}\)
- Xét tam giác vuông II’J: \(II' = JI'.{\mathop{\rm t}\nolimits} {\rm{anr}} = e.{\mathop{\rm t}\nolimits} {\rm{anr}}\)
=> \(MK = \dfrac{{e.{\mathop{\rm t}\nolimits} {\rm{anr}}}}{{\tan i}}\)
=> \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\)
Với góc tới i nhỏ ta có: \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\~e.(1 - \dfrac{{{\rm{Sin r}}}}{{Sini}}) = e.(1 - \dfrac{{{n_1}}}{{{n_2}}})\)
- Thay số: \(e = 6cm;{n_1} = 1;{n_2} = 1,5 \to SS' = 6.(1 - \dfrac{1}{{1,5}}) = 2cm\)
Ảnh \(S'\) của \(S\) qua bản hai mặt song song cách \(S\) một khoảng:

- Độ dời ảnh: SS’ = IM = IK – MK = e – MK
- Xét tam giác vuông MKJ: \(MK = \dfrac{{KJ}}{{\tan i}} = \dfrac{{II'}}{{\tan i}}\)
- Xét tam giác vuông II’J: \(II' = JI'.{\mathop{\rm t}\nolimits} {\rm{anr}} = e.{\mathop{\rm t}\nolimits} {\rm{anr}}\)
=> \(MK = \dfrac{{e.{\mathop{\rm t}\nolimits} {\rm{anr}}}}{{\tan i}}\)
=> \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\)
Với góc tới i nhỏ ta có: \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\~e.(1 - \dfrac{{{\rm{Sin r}}}}{{Sini}}) = e.(1 - \dfrac{{{n_1}}}{{{n_2}}})\)
- Thay số: \(e = 6cm;{n_1} = 1;{n_2} = 1,5 \to SS' = 6.(1 - \dfrac{1}{{1,5}}) = 2cm\)
Mắt đặt trong không khí, chiều dài lớn nhất của OA để mắt không thấy đầu A là
- Mắt không nhìn thấy đầu A khi tia sáng tới từ A tới mặt nước bị phản xạ toàn phần
=> \(i \ge {i_{gh}}\) với \(sin{i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{4/3}} = \dfrac{3}{4} \to {i_{gh}} = {48^0}35'\)
- Xét tam giác vuông OAI: \(tani = \dfrac{{OI}}{{OA}} = \dfrac{4}{{OA}} \to OA = \dfrac{4}{{\tan i}}\)
- OAmax suy ra: tani min imin = igh => \(O{A_{\max }} = \frac{4}{{\tan {i_{gh}}}} = \frac{4}{{\tan ({{48}^0}35')}} = 3,53cm\)
Mắt đặt trong không khí sẽ thấy đầu A cách mặt nước một khoảng lớn nhất là:
- tia sáng từ A truyền trong nước rồi khúc xạ ra không khí, mắt ta nhìn thấy là ảnh A’ của A (Ảnh A’ gần mặt nước hơn A)
- Áp dụng biểu thức định luật khúc xạ ánh sáng ta có: \({n_1}.sini = {n_2}.sinr\)
=> \(1,33.sini = sinr\)
=> góc tới i càng nhỏ thì góc khúc xạ r càng nhỏ, góc khúc xạ r càng nhỏ thì ảnh A’ càng xa O => Ảnh A’ xa O nhất được cho bởi tia sáng AI đi sát mép miếng gỗ
- Tính OAmax’
+ Xét tam giác vuông OIA’: \(OA{'_{\max }} = \dfrac{{OI}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{R}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{4}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}}\)
+ Lại có: \(1,33.sini = sinr\)
Xét tam giác vuông OAI: \(sini = \dfrac{{OI}}{{OA}} = \dfrac{4}{{\sqrt {{4^2} + {6^2}} }} = \dfrac{2}{{\sqrt {13} }}\)
=> \(sinr = 1,33.\dfrac{2}{{\sqrt {13} }} \to r = {47,69^0}\)
=> \(OA{'_{\max }} = \dfrac{4}{{{\mathop{\rm t}\nolimits} {\rm{an(47}}{\rm{,69)}}}} = 3,64cm\)
Mắt đặt trong không khí sẽ thấy đầu A cách mặt nước một khoảng lớn nhất là:
- tia sáng từ A truyền trong nước rồi khúc xạ ra không khí, mắt ta nhìn thấy là ảnh A’ của A (Ảnh A’ gần mặt nước hơn A)
- Áp dụng biểu thức định luật khúc xạ ánh sáng ta có: \({n_1}.sini = {n_2}.sinr\)
=> \(1,33.sini = sinr\)
=> góc tới i càng nhỏ thì góc khúc xạ r càng nhỏ, góc khúc xạ r càng nhỏ thì ảnh A’ càng xa O => Ảnh A’ xa O nhất được cho bởi tia sáng AI đi sát mép miếng gỗ
- Tính OAmax’
+ Xét tam giác vuông OIA’: \(OA{'_{\max }} = \dfrac{{OI}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{R}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{4}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}}\)
+ Lại có: \(1,33.sini = sinr\)
Xét tam giác vuông OAI: \(sini = \dfrac{{OI}}{{OA}} = \dfrac{4}{{\sqrt {{4^2} + {6^2}} }} = \dfrac{2}{{\sqrt {13} }}\)
=> \(sinr = 1,33.\dfrac{2}{{\sqrt {13} }} \to r = {47,69^0}\)
=> \(OA{'_{\max }} = \dfrac{4}{{{\mathop{\rm t}\nolimits} {\rm{an(47}}{\rm{,69)}}}} = 3,64cm\)
Phát biểu nào sau đây là đúng?
A, D – sai vì chiết suất tỉ đối giữa 2 môi trường là tỉ số giữa 2 chiết suất tuyệt đối của 2 môi trường đó: \({{\rm{n}}_{{\rm{21}}}}{\rm{ = }}\dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}}\)nếu \({{\rm{n}}_{{\rm{21}}}}{\rm{ > 1 = > }}\dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}} > 1 = > {{\rm{n}}_{\rm{2}}} > {{\rm{n}}_1}\) ; \(\)
B - sai vì chiết suất tuyệt đối của chân không là 1, của mọi môi trường trong suốt khác đều lớn hơn 1.
C - đúng vì chiết suất tỉ đối giữa 2 môi trường là tỉ số giữa 2 chiết suất tuyệt đối của 2 môi trường đó: \({{\rm{n}}_{{\rm{21}}}}{\rm{ = }}\dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}}\)
Với một tia sáng đơn sắc, chiết suất tuyệt đối của nước là \({n_1}\), của thủy tinh là \({n_2}\). Chiết suất tỉ đối khi tia sáng đó truyền từ nước sang thủy tinh là:
- Chiết suất tỉ đối khi tia sáng truyền từ nước sang thủy tinh là: \({{\rm{n}}_{{\rm{21}}}}{\rm{ = }}\dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}}\)
Khi có hiện tượng phản xạ thì tia tới và tia phản xạ
- Tia tới và tia phản xạ cùng nằm trong một môi trường truyền sáng
Trong hiện tượng khúc xạ ánh sáng
A,B – sai vì phụ thuộc vào \({{\rm{n}}_{{\rm{21}}}}\): Nếu \({{\rm{n}}_{{\rm{21}}}} > 1\): góc khúc xạ bé hơn góc tới ; Nếu \({{\rm{n}}_{{\rm{21}}}} < 1\): góc khúc xạ lớn hơn góc tới
C – sai vì góc tới i và góc khúc xạ r không tỉ luận với nhau mà chỉ có i tăng thì r cũng tăng; sin i và sin r thì tỉ lệ thuận
D – đúng vì góc tới i tăng thì góc khúc xạ r cũng tăng
Khi xảy ra hiện tượng khúc xạ ánh sáng thì quan hệ giữa góc tới và góc khúc xạ tuân theo quy luật:
Khi xảy ra hiện tượng khúc xạ ánh sáng thì quan hệ giữa góc tới và góc khúc xạ tuân theo qui luật hàm sin
Chiết suất tỉ đối giữa môi trường khúc xạ với môi trường tới
A,B – sai vì chiết suất tỉ đối giữa 2 môi trường có thể lớn hơn 1 hoặc nhỏ hơn 1: \({{\rm{n}}_{{\rm{21}}}}{\rm{ > 1 }} \Leftrightarrow \dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}} > 1 \Leftrightarrow {{\rm{n}}_{\rm{2}}} > {{\rm{n}}_1}\) ; \({{\rm{n}}_{{\rm{21}}}}{\rm{ < 1 }} \Leftrightarrow \dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}} < 1 \Leftrightarrow {{\rm{n}}_{\rm{2}}}{\rm{ < }}{{\rm{n}}_1}\)
C – đúng vì chiết suất tỉ đối giữa 2 môi trường là tỉ số giữa 2 chiết suất tuyệt đối của 2 môi trường đó: \({{\rm{n}}_{{\rm{21}}}}{\rm{ = }}\dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}}\)
D – sai
Khi ánh sáng truyền từ môi trường 1 sang môi trường 2 thì ta sẽ nói môi trường 2 kém chiết quang hơn môi trường 1 nếu chiết suất tỉ đối:
B – đúng vì môi trường 2 kém chiết quang hơn môi trường 1 \( \Leftrightarrow {{\rm{n}}_{\rm{2}}}{\rm{ < }}{{\rm{n}}_1}{\rm{ }} \Leftrightarrow \dfrac{{{{\rm{n}}_2}}}{{{{\rm{n}}_{\rm{1}}}}} < 1 \Leftrightarrow {{\rm{n}}_{{\rm{21}}}}{\rm{ < 1}}\)
A,C, D - sai
Khi tia sáng đi từ môi trường trong suốt \({n_1}\) tới mặt phân cách với môi trường trong suốt \({n_2}\) (với \({n_2} > {n_1}\)), tia sáng không vuông góc với mặt phân cách thì:
A,B – sai vì Hiện tượng khúc xạ ánh sáng luôn kèm theo hiện tượng phản xạ một phần
D – đúng
C – sai vì Điều kiện xảy ra hiện tượng PXTP: \({{\rm{n}}_{\rm{2}}}{\rm{ < }}{{\rm{n}}_1}{\rm{ ; sin i > sin }}{{\rm{i}}_{_{{\rm{gh}}}}}\)

