Hai điện tích \({q_1} = - q;{q_2} = 4q\) đặt cách nhau một khoảng r. Nếu điện tích \({q_1}\) tác dụng lực điện lên điện tích \({q_2}\) có độ lớn là F thì lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) có độ lớn là:
Theo định luật Cu-lông ta có: Lực tác dụng của điện tích \({q_1}\) lên \({q_2}\) và lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) bằng nhau: \({F_{12}} = {F_{21}} = F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Lực tương tác tĩnh điện giữa hai điện tích điểm đứng yên đặt cách nhau một khoảng \(2cm\) là \(F\). Nếu để chúng cách nhau \(4cm\) thì lực tương tác giữa chúng là
Ta có:
+ Khi \({r_1} = 2cm\): Lực tương tác tĩnh điện giữa hai điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_1}^2}}\)
+ Khi \({r_2} = 4cm\): Lực tương tác tĩnh điện giữa hai điện tích: \(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_2}^2}}\)
\(\begin{array}{l} \to \dfrac{{F'}}{F} = \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{{{({{2.10}^{ - 2}})}^2}}}{{{{({{4.10}^{ - 2}})}^2}}} = \dfrac{1}{4}\\ \to F' = \dfrac{F}{4}\end{array}\)
Hai điện tích điểm đứng yên trong không khí cách nhau một khoảng r tác dụng lên nhau lực có độ lớn bằng F. Khi đưa chúng vào trong dầu hoả có hằng số điện môi \(\varepsilon = 2\) và tăng khoảng cách giữa chúng lên \(2r\) thì độ lớn của lực tương tác giữa chúng là
Theo định luật Cu-lông, ta có: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Khi 2 điện tích đặt trong không khí, \(\varepsilon = 1\): \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Khi đặt 2 điện tích vào trong dầu có \(\varepsilon = 2\), và \(r' = 2r\) : \(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon r{'^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{2.{{\left( {2r} \right)}^2}}} = \dfrac{1}{8}k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = \dfrac{1}{8}F\)
Hai điện tích điểm được đặt cố định trong một bình không khí thì lực tương tác giữa chúng là 12N. Khi đổ đầy một chất lỏng cách điện vào bình thì lực tương tác giữa chúng là 4N. Hằng số điện môi của chất lỏng này là:
Ta có:
\(\left\{ \begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = 12\\F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = 4\end{array} \right. \Rightarrow \dfrac{F}{{F'}} = \varepsilon = \dfrac{{12}}{4} = 3\)
Quả cầu A có điện tích \( - 3,{2.10^{ - 7}}C\) và đặt cách quả cầu B có điện tích \(2,{4.10^{ - 7}}C\) một khoảng \(12cm\). Lực tương tác giữa hai quả cầu khi đặt trong không khí là
Ta có \({q_1}{q_2} < 0\) \( \Rightarrow \) 2 quả cầu hút nhau
Lực hút giữa hai quả cầu: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\dfrac{{\left| { - 3,{{2.10}^{ - 7}}.2,{{4.10}^{ - 7}}} \right|}}{{1.{{\left( {{{12.10}^{ - 2}}} \right)}^2}}} = 0,048N = 48mN\)
Hai quả cầu nhỏ có điện tích \(2\mu C\) và \(6\mu C\), tương tác với nhau một lực \(0,1N\) trong chân không. Khoảng cách giữa chúng là:
Theo định luật Cu-lông, ta có: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
- Đặt trong chân không \( \Rightarrow \varepsilon = 1\)
\(\begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\ \Rightarrow r = \sqrt {k\dfrac{{\left| {{q_1}{q_2}} \right|}}{F}} = \sqrt {{{9.10}^9}\dfrac{{\left| {{{2.10}^{ - 6}}{{.6.10}^{ - 6}}} \right|}}{{0,1}}} = \dfrac{{3\sqrt 3 }}{5}m\end{array}\)
Hai điện tích \({q_1}\) và \({q_2}\) đặt cách nhau \(20cm\) trong không khí, chúng đẩy nhau với một lực \(F = 1,8N\). Biết \({q_1} + {q_2} = - {6.10^{ - 6}}C\) và \(\left| {{q_1}} \right| > \left| {{q_2}} \right|\). Xác định loại điện tích và giá trị của \({q_1}\) và \({q_2}\)
+ Ta có, lực tương tác giữa hai điện tích điểm:
\(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
\( \to \left| {{q_1}{q_2}} \right| = \dfrac{{F.{r^2}}}{{\varepsilon k}} = \dfrac{{1,8.{{(0,2)}^2}}}{{{{1.9.10}^9}}} = {8.10^{ - 12}}\)
Do \({q_1},{q_2}\) đẩy nhau nên ta suy ra \({q_1}{q_2} = {8.10^{ - 12}}\) (1)
+ Mặt khác, \({q_1} + {q_2} = - {6.10^{ - 6}}C\) (2)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{q_1}{q_2} = {8.10^{ - 12}}\\{q_1} + {q_2} = - {6.10^{ - 6}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{q_1} = - {4.10^{ - 6}}C\\{q_2} = - {2.10^{ - 6}}C\end{array} \right.\)
Hai điện tích điểm giống nhau đặt trong chân không cách nhau một đoạn \(4cm\), lực đẩy tĩnh điện giữa chúng là \({10^{ - 5}}N\). Tìm khoảng cách giữa chúng để lực đẩy tĩnh điện giữa chúng là \(2,{5.10^{ - 6}}N\)
Do hai điện tích điểm giống nhau , ta suy ra \({q_1} = {q_2} = q\)
+ Khi khoảng cách giữa hai điện tích \({r_1} = 4cm = 0,04m\) thì \({F_1} = k\dfrac{{{q^2}}}{{r_1^2}} = {10^{ - 5}}N\)
Suy ra: \({q^2} = \dfrac{{F.r_1^2}}{k} = \dfrac{{{{10}^{ - 5}}.0,{{04}^2}}}{{{{9.10}^9}}} = \dfrac{{16}}{9}{.10^{ - 18}}\)
+ Khi khoảng cách giữa hai điện tích là \({r_2}\) thì \({F_2} = k\dfrac{{{q^2}}}{{r_2^2}} = 2,{5.10^{ - 6}}N\)
Suy ra:
\(\begin{array}{l}r_2^2 = \dfrac{{k{q^2}}}{F} = \dfrac{{{{9.10}^9}.\dfrac{{16}}{9}{{.10}^{ - 18}}}}{{2,{{5.10}^{ - 6}}}} = 6,{4.10^{ - 3}}\\ \Rightarrow {r_2} = 0,08m = 8cm\end{array}\)
Đặt 2 điện tích \({q_1}\) và \({q_2}\) trong không khí. Lực hút tĩnh điện giữa hai điện tích là \({5.10^{ - 7}}N\). Khi đưa chúng lại gần nhau thêm \(2cm\) thì lực hút là \({2.10^{ - 6}}N\). Khoảng cách ban đầu giữa chúng là
Ta có:
+ Khi khoảng cách giữa hai điện tích \(r\): \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {5.10^{ - 7}}N\)
+ Khi đưa chúng ra lại gần nhau thêm \(2cm\) thì khoảng cách giữa hai điện tích lúc này là \(r' = r - 0,02\), khi đó:
\(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{r{'^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{{(r - 0,02)}^2}}} = {2.10^{ - 6}}N\)
\(\begin{array}{l} \to \dfrac{F}{{F'}} = \dfrac{{r{'^2}}}{{{r^2}}} = \dfrac{{{{(r - 0,02)}^2}}}{{{r^2}}} = \dfrac{{{{5.10}^{ - 7}}}}{{{{2.10}^{ - 6}}}} = \dfrac{1}{4}\\ \to r - 0,02 = \dfrac{{\rm{r}}}{2}\\ \to r = 0,04m = 4cm\end{array}\)
Hai vật nhỏ giống nhau, mỗi vật thừa 1 electron. Tìm khối lượng mỗi vật để lực tĩnh điện bằng lực hấp dẫn.
Ta có:
- \({q_1} = {q_2} = 1e = - 1,{6.10^{ - 19}}C = q\)
- Lực đẩy giữa hai prôtôn: \({F_1} = k\dfrac{{{q^2}}}{{{r^2}}}\)
- Lực hấp dẫn giữa hai prôtôn:\({F_2} = G\dfrac{{{m^2}}}{{{r^2}}}\)
Để lực tĩnh điện bằng lực hấp dẫn:
\(\begin{array}{l}{F_1} = {F_2} \Leftrightarrow k\dfrac{{{q^2}}}{{{r^2}}} = G\dfrac{{{m^2}}}{{{r^2}}}\\ \Rightarrow m = \sqrt {\dfrac{k}{G}} \left| q \right| = \sqrt {\dfrac{{{{9.10}^9}}}{{6,{{67.10}^{ - 11}}}}} 1,{6.10^{ - 19}} = 1,{86.10^{ - 9}}kg\end{array}\)
Cho \({q_1} = {q_2} = {10^{ - 6}}C\) đặt tại A, B cách nhau \(10cm\). Đặt một điện tích \({q_3} = {5.10^{ - 6}}C\) tại C sao cho \({q_3}\) cách \({q_1}\) một đoạn \(10cm\), cách \({q_2}\) một đoạn \(15cm\) . Tính lực tác dụng tổng hợp lên \({q_3}\)
Vị trí các điện tích như hình vẽ.
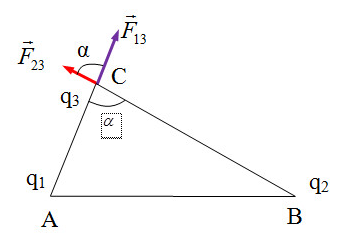
Áp dụng định lí hàm số cos trong tam giác ABC, ta có:
\(cos\alpha = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}} = \dfrac{{{{10}^2} + {{15}^2} - {{10}^2}}}{{2.10.15}} = \dfrac{3}{4}\)
Ta có, các lực tác dụng lên \({q_3}\) gồm:
+ Lực do \({q_1}\) tác dụng lên \({q_3}\): \({F_{13}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_{13}^2}} = {9.10^9}\dfrac{{\left| {{{10}^{ - 6}}{{.5.10}^{ - 6}}} \right|}}{{0,{1^2}}} = 4,5N\)
+ Lực do \({q_2}\) tác dụng lên \({q_3}\): \({F_{23}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{r_{23}^2}} = {9.10^9}\dfrac{{{{10}^{ - 6}}{{.5.10}^{ - 6}}}}{{0,{{15}^2}}} = 2N\)
Lực tổng hợp tại \({q_3}\): \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Về độ lớn:
\(\begin{array}{l}F_3^2 = F_{13}^2 + F_{23}^2 + 2{F_{13}}{F_{23}}cos\left( {\widehat {\overrightarrow {{F_{13}}} ,\overrightarrow {{F_{23}}} }} \right)\\ = 4,{5^2} + {2^2} + 2.4,5.2.\dfrac{3}{4}\\ \Rightarrow {F_3} \approx 6,144N\end{array}\)
Cho \({q_1} = {q_2} = {10^{ - 6}}C\) đặt tại A, B cách nhau \(10cm\). Đặt một điện tích \({q_3} = {5.10^{ - 6}}C\) tại C sao cho tam giác ABC là tam giác đều. Tính lực tác dụng tổng hợp lên \({q_3}\)
Ta có: \(\Delta ABC\) đều, suy ra: \(AB = AC = BC = 10cm = 0,1m\)
- Các điện tích q1 và q2 tác dụng lên điện tích q3 các lực và có phương chiều như hình vẽ:
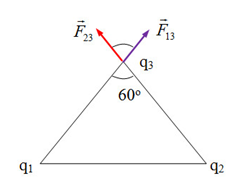
Có độ lớn: \({F_{13}} = {F_{23}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_{13}^2}} = {9.10^9}\dfrac{{\left| {{{10}^{ - 6}}{{.5.10}^{ - 6}}} \right|}}{{0,{1^2}}} = 4,5N\)
Lực tổng hợp tại \({q_3}\): \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Về độ lớn:
\(\begin{array}{l}F_3^2 = F_{13}^2 + F_{23}^2 + 2{F_{13}}{F_{23}}cos\left( {\widehat {\overrightarrow {{F_{13}}} ,\overrightarrow {{F_{23}}} }} \right)\\ = 4,{5^2} + 4,{5^2} + 2.4,5.4,5.cos{60^0}\\ = 4,{5^2}.3\\ \Rightarrow {F_3} = 4,5\sqrt 3 N\end{array}\)
Ba điện tích điểm \({q_1} = {27.10^{ - 8}}C\), \({q_2} = {64.10^{ - 8}}C\), \({q_3} = - {10^{ - 7}}C\) đặt trong không khí lần lượt tại ba đỉnh của một tam giác vuông tại C. Cho \(AC = 30cm\), \(BC = 40cm\). Xác định độ lớn lực tác dụng lên \({q_3}\)
.png)
Ta có:
\({r_{13}} = AC = 30cm = 0,3m\)
\({r_{23}} = BC = 40cm = 0,4m\)
Các điện tích \({q_1}\) và \({q_2}\) tác dụng lên điện tích \({q_3}\) các lực \(\overrightarrow {{F_{13}}} \) và \(\overrightarrow {{F_{23}}} \) có phương chiều như hình vẽ, có độ lớn:
\({F_{13}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_{13}^2}} = {9.10^9}\dfrac{{\left| {{{27.10}^{ - 8}}.\left( { - {{10}^{ - 7}}} \right)} \right|}}{{0,{3^2}}} = 2,{7.10^{ - 3}}N\)
\({F_{23}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{r_{23}^2}} = {9.10^9}\dfrac{{\left| {{{64.10}^{ - 8}}\left( { - {{10}^{ - 7}}} \right)} \right|}}{{0,{4^2}}} = 3,{6.10^{ - 3}}N\)
Lực tổng hợp do \({q_1}\) và \({q_2}\) tác dụng lên \({q_3}\) là: \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Có độ lớn: \({F_3} = \sqrt {F_{13}^2 + F_{23}^2} = \sqrt {{{\left( {2,{{7.10}^{ - 3}}} \right)}^2} + {{\left( {3,{{6.10}^{ - 3}}} \right)}^2}} = 4,{5.10^{ - 3}}N\)
(Do \(\overrightarrow {{F_{13}}} \bot \overrightarrow {{F_{23}}} \))
Cho hai điện tích điểm đặt trong chân không. Khi khoảng cách giữa hai điện tích là \(r\) thì lực tương tác điện giữa chúng có độ lớn là \(F\). Khi khoảng cách giữa hai điện tích là \(3r\) thì lực tương tác điện giữa chúng có độ lớn là:
Ta có:
+ Khi khoảng cách giữa hai điện tích điểm là r: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Khi khoảng cách giữa hai điện tích điểm là 3r: \(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {{\left( {3r} \right)}^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{9\varepsilon {r^2}}}\)
=> \(\dfrac{F}{{F'}} = 9 \to F' = \dfrac{F}{9}\)
Hai điện tích dương \({q_1} = {q_2} = 49\mu C\) đặt cách nhau một khoảng d trong không khí. Gọi M là vị trí tại đó, lực tổng hợp tác dụng lên điện tích q0 bằng 0. Điểm M cách q1 một khoảng
M là vị trí tại đó lực tổng hợp tác dụng lên điện tích q0 = 0 nên:
\(\begin{array}{l}{F_{1M}} = {F_{2M}} \Leftrightarrow k\dfrac{{\left| {q.{q_0}} \right|}}{{r_{1M}^2}} = k\dfrac{{\left| {q.{q_0}} \right|}}{{r_{2M}^2}}\\ \Rightarrow r_{1M}^2 = r_{2M}^2 \Leftrightarrow {r_{1M}} = {r_{2M}}\end{array}\)
=> M là trung điểm của đoạn thẳng nối q1 và q2 => M cách q1 một khoảng d/2.
Khi tăng đồng thời độ lớn của hai điện tích điểm và khoảng cách giữa chúng lên bốn lần thì lực tương tác giữa chúng?
Lực tương tác giữa hai điện tích điểm: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Rightarrow \left\{ \begin{array}{l}F \sim \left| {{q_1}{q_2}} \right|\\F \sim \frac{1}{{{r^2}}}\end{array} \right.\)
Tăng độ lớn của hai điện tích và khoảng cách giữa chúng lên \(4\) lần
→ lực tương tác giữa hai điện tích không thay đổi
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng hai sợi dây không dãn, dài 10 cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600. Tính độ lớn điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s2).
Khi quả cầu cân bằng thì: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_d}} = 0\)
Đặt \(\overrightarrow {T'} = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow {T'} + \overrightarrow T = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow \downarrow \overrightarrow T \\T' = T\end{array} \right.\)
Biểu diễn các lực tác dụng lên quả cầu:
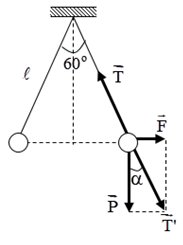
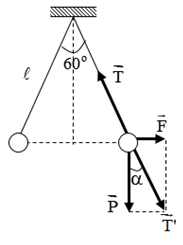
+ Từ hình vẽ ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 30 = 0,029N\end{array}\)
+ Khi hai dây treo hợp với nhau một góc 600thì khoảng cách giữa hai điện tích bằng:
\(l = 10cm = 0,1m\)
+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{l^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{l^2}}}{k}} \)
Thay số ta được: \(\left| q \right| = \sqrt {\dfrac{{0,029.0,{1^2}}}{{{{9.10}^9}}}} = 1,{8.10^{ - 7}}C\)
+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2.\left| q \right| = 3,{6.10^{ - 7}}\;C\)
Khoảng cách giữa một proton và một electron trong một nguyên tử là \(5.10^{-9}cm\). Coi proton và electron là các điện tích điểm, lấy \(e = 1,6.10^{-19}C\). Lực tương tác điện giữa chúng là
Lực tương tác điện giữa electron và proton có độ lớn:\(F = k\dfrac{{{e^2}}}{{{r^2}}} = {9.10^9}.\dfrac{{{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{{{({{5.10}^{ - 11}})}^2}}} = 9,{216.10^{ - 8}}N\)
Hai điện tích \({q_1} = {4.10^{ - 6}}C\) và \({q_2} = {16.10^{ - 6}}C\) đặt tại hai điểm A và B trong không khí cách nhau 30 cm. Xác định độ lớn của lực tác dụng của q1 lên q2.
Lực điện tác dụng của q1 lên q2 là:
\(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {9.10^9}.\dfrac{{\left| {{{4.10}^{ - 6}}{{.16.10}^{ - 6}}} \right|}}{{{{\left( {{{30.10}^{ - 2}}} \right)}^2}}} = 6,4N\)
Trong không khí hai quả cầu nhỏ cùng khối lượng 0,3g được treo vào một điểm bằng hai sợi dây nhẹ cách điện có độ dài bằng nhau. Cho hai quả cầu nhiễm điện thì chúng đẩy nhau. Khi hai quả cầu cân bằng, hai dây treo hợp với nhau một góc 600. Lấy g = 10 m/s2. Tính độ lớn lực tương tác tĩnh điện giữa hai quả cầu
Phân tích các lực tác dụng lên quả cầu:
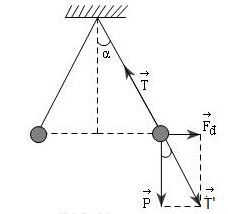
Khi quả cầu cân bằng thì: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_d}} = 0\)
Đặt \(\overrightarrow {T'} = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow {T'} + \overrightarrow T = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow \downarrow \overrightarrow T \\T' = T\end{array} \right.\)
Hai dây treo hợp với nhau một góc 600\( \Rightarrow \alpha = {30^0}\)
Từ hình vẽ ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha = mg.\tan \alpha \\ \Rightarrow {F_d} = 0,{3.10^{ - 3}}.10.\tan 30 = 1,{73.10^{ - 3}}N\end{array}\)

