Câu hỏi:
2 năm trước
Cho \({q_1} = {q_2} = {10^{ - 6}}C\) đặt tại A, B cách nhau \(10cm\). Đặt một điện tích \({q_3} = {5.10^{ - 6}}C\) tại C sao cho \({q_3}\) cách \({q_1}\) một đoạn \(10cm\), cách \({q_2}\) một đoạn \(15cm\) . Tính lực tác dụng tổng hợp lên \({q_3}\)
Trả lời bởi giáo viên
Đáp án đúng: a
Vị trí các điện tích như hình vẽ.
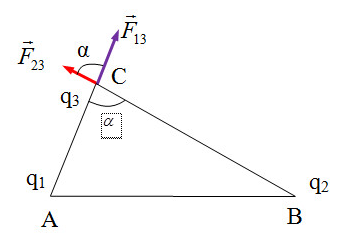
Áp dụng định lí hàm số cos trong tam giác ABC, ta có:
\(cos\alpha = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}} = \dfrac{{{{10}^2} + {{15}^2} - {{10}^2}}}{{2.10.15}} = \dfrac{3}{4}\)
Ta có, các lực tác dụng lên \({q_3}\) gồm:
+ Lực do \({q_1}\) tác dụng lên \({q_3}\): \({F_{13}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_{13}^2}} = {9.10^9}\dfrac{{\left| {{{10}^{ - 6}}{{.5.10}^{ - 6}}} \right|}}{{0,{1^2}}} = 4,5N\)
+ Lực do \({q_2}\) tác dụng lên \({q_3}\): \({F_{23}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{r_{23}^2}} = {9.10^9}\dfrac{{{{10}^{ - 6}}{{.5.10}^{ - 6}}}}{{0,{{15}^2}}} = 2N\)
Lực tổng hợp tại \({q_3}\): \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
Về độ lớn:
\(\begin{array}{l}F_3^2 = F_{13}^2 + F_{23}^2 + 2{F_{13}}{F_{23}}cos\left( {\widehat {\overrightarrow {{F_{13}}} ,\overrightarrow {{F_{23}}} }} \right)\\ = 4,{5^2} + {2^2} + 2.4,5.2.\dfrac{3}{4}\\ \Rightarrow {F_3} \approx 6,144N\end{array}\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Phương pháp tổng hợp lực
+ Vận dụng hệ thức lượng trong tam giác
