Một khung dây dẫn hình vuông cạnh a = 6 cm; đặt trong từ trường đều B = 4.10-3 T, đường sức từ trường vuông góc với mặt phẳng khung dây. Cầm hai cạnh đối diện hình vuông kéo về hai phía để được hình chữ nhật có cạnh này dài gấp đôi cạnh kia trong khoảng thời gian 10-6s. Độ lớn suất điện động cảm ứng xuất hiện trong khung là:
Diện tích hình vuông: \({S_1} = {a^2}\; = 0,{06^2}\; = 3,{6.10^{ - 3}}\;\left( {{m^2}} \right)\)
Chu vi của hình vuông \(C = 4a = 4.6 = 24cm\)
Cầm hai cạnh đối diện hình vuông kéo về hai phía để được hình chữ nhật có cạnh này dài gấp đôi cạnh kia. Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là b và c. Ta có:
\(\left\{ \begin{array}{l}b = 2c\\2\left( {b + c} \right) = 24cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 8cm\\c = 4cm\end{array} \right.\)
Diện tích hình chữ nhật: \({S_2} = b.c\; = 0,08.0,04 = 3,{2.10^{ - 3}}\;\left( {{m^2}} \right)\)
→ Suất điện động cảm ứng xuất hiện trong khung:
\({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = B.\cos 0.\left| {\dfrac{{\Delta S}}{{\Delta t}}} \right| = {4.10^{ - 3}}.\dfrac{{\left( {3,6 - 3,2} \right){{.10}^{ - 3}}}}{{{{10}^{ - 6}}}}\; = 1,6\,\,\left( V \right)\)
Một khung dây hình tròn bán kính 20 cm nằm toàn bộ trong một từ trường đều mà các đường sức từ vuông với mặt phẳng vòng dây. Trong thời gian t cảm ứng từ tăng từ 0,1 T đến 1,1 T thì trong khung dây có một suất điện động không đổi với độ lớn là 0,2 V. Thời gian t đó là
Đường sức từ vuông góc với mặt phẳng vòng dây \( \Rightarrow \alpha = \left( {\overrightarrow n ;\overrightarrow B } \right) = {0^0}\)
Độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là:
\(\begin{array}{l}{e_c} = \left| { - \dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{{\Phi _1} - {\Phi _2}}}{{\Delta t}}} \right| = \dfrac{{\left| {NS.\cos \alpha .\left( {{B_1} - {B_2}} \right)} \right|}}{{\Delta t}} = \dfrac{{\left| {N.\pi {r^2}.\cos \alpha .\left( {{B_1} - {B_2}} \right)} \right|}}{{\Delta t}}\\ \Rightarrow \Delta t = \dfrac{{\left| {N.\pi {r^2}.\cos \alpha .\left( {{B_1} - {B_2}} \right)} \right|}}{{{e_c}}} = \dfrac{{1.\pi .0,{2^2}.\cos 0.\left( {0,1 - 1,1} \right)}}{{0,2}} = 0,2\pi \,\,\left( s \right)\end{array}\)
Một hình vuông cạnh 5cm được đặt trong từ trường đều B = 0,01 T. Đường sức từ vuông góc với mặt phẳng khung. Quay khung trong 10-3 s để mặt phẳng khung dây song song với đường sức từ. Suất điện động trung bình xuất hiện trong khung là:
Ta có: \(\Phi = NBS.\cos \alpha ;\,\,\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right)\)
Tại thời điểm t đường sức từ vuông góc với mặt phẳng khung dây \( \Rightarrow {\alpha _1} = \left( {\overrightarrow n ;\overrightarrow B } \right) = {0^0}\)
Tại thời điểm t + 10-3s, mặt phẳng khung dây song song với đường sức từ \( \Rightarrow {\alpha _2} = \left( {\overrightarrow n ;\overrightarrow B } \right) = {90^0}\)
Suất điện động xuất hiện trong khung là:
\(\begin{array}{l}{e_c} = - \dfrac{{\Delta \Phi }}{{\Delta t}} = -\dfrac{{{\Phi _2} - {\Phi _1}}}{{\Delta t}} = \dfrac{{NBS.\left( {\cos {\alpha _1} - \cos {\alpha _2}} \right)}}{{\Delta t}}\\\,\,\,\,\, = \dfrac{{1.0,01.0,{{05}^2}.\left( {\cos 0 - \cos 90} \right)}}{{{{10}^{ - 3}}}} = 0,025V = 25mV\end{array}\)
Một vòng dây dẫn tròn có diện tích \(0,4\,\,{m^2}\) đặt trong từ trường đều có cảm ứng từ \(B = 0,6\,\,T\), vecto cảm ứng từ vuông góc với mặt phẳng vòng dây. Nếu cảm ứng từ tăng đến \(1,4\,\,T\) trong thời gian \(0,25\,\,s\) thì độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là
Độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là:
\({e_c} = \left| { - \frac{{\Delta \Phi }}{{\Delta t}}} \right| = \frac{{S.\left| {\Delta B} \right|}}{{\Delta t}} = \frac{{0,4.\left| {1,4 - 0,6} \right|}}{{0,25}} = 1,28\,\,\left( V \right)\)
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh \(MN\) có chiều dài \(1m\) có điện trở \(R = 5\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ, độ lớn \(B{\rm{ }} = {\rm{ }}0,1T\)
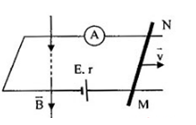
Ampe kế chỉ bao nhiêu khi \(MN\) đứng yên?
Hướng dẫn giải:
Khi \(MN\) đứng yên, thì trong mạch không có dòng điện cảm ứng , nên số chỉ của ampe kế là:
\(I = \frac{E}{{R + r}} = \frac{{1,5}}{{5 + 0,1}} = 0,29A\)
Một khung dây cứng phẳng diện tích 25 cm2 gồm 10 vòng dây, đặt trong từ trường đều, mặt phẳng khung vuông góc với các đường cảm ứng từ. Cảm ứng từ biến thiên theo thời gian như đồ thị hình vẽ. Tính suất điện động cảm ứng xuất hiện trong khung kể từ t = 0 đến t = 0,4 (s):
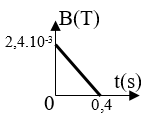
Mặt phẳng khung vuông góc với các đường cảm ứng từ → α = 00
Suất điện động xuất hiện trong khung kể từ t = 0 đến t = 0,4s là:
\(\begin{array}{l}{e_c} = - \dfrac{{\Delta \Phi }}{{\Delta t}} = \dfrac{{{\Phi _1} - {\Phi _2}}}{{\Delta t}} = \dfrac{{NS.\cos \left( {{B_1} - {B_2}} \right)}}{{\Delta t}}\\\,\,\,\,\, = \dfrac{{{{10.25.10}^{ - 4}}.\cos 0.\left( {2,{{4.10}^{ - 3}} - 0} \right)}}{{0,4}} = 1,{5.10^{ - 4}}V\end{array}\)
Một cuộn dây tròn gồm 1000 vòng dây, có diện tích 40 cm2 đặt trong một từ trường đều có véc tơ cảm ứng từ vuông góc với mặt phẳng vòng dây. Trong thời gian ∆t = 0,02 giây, độ lớn của cảm ứng từ tăng đều từ 0 T đến 4.10-3 T. Xác định độ lớn suất điện động cảm ứng xuất hiện trong cuộn dây.
Độ lớn suất điện động cảm ứng trong cuộn dây là:
\(\left| {{e_c}} \right| = N\left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = NS\dfrac{{\left| {\Delta B} \right|}}{{\Delta t}} = {1000.40.10^{ - 4}}.\dfrac{{\left| {{{4.10}^{ - 3}} - 0} \right|}}{{0,02}} = 0,8\,\,\left( V \right)\)
Một khung dây hình chữ nhật ABCD chuyển động theo phương vuông góc với dòng điện thẳng dài vô hạn như hình vẽ. Dòng điện cảm ứng trong khung:
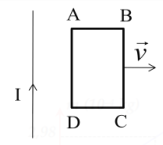
Cảm ứng từ ban đầu do dòng điện I ở vị trí khung dây ABCD có chiều đi vào.
Khi khung dây di chuyển ra xa dòng điện như hình vẽ thì cảm ứng từ giảm dần, nghĩa là từ thông xuyên qua khung dây giảm dần.
Do đó, theo định luật Len xơ thì từ trường cảm ứng phải cùng chiều với từ trường ban đầu, nghĩa là hướng vào.
Dùng quy tắc nắm tay phải ta xác định được chiều dòng điện cảm ứng là ABCDA
Suất điện động cảm ứng là suất điện động
Suất điện động sinh ra dòng điện cảm ứng trong mạch điện kín là suất điện động cảm ứng
Một ống dây điện thẳng dài bán kính 25 mm có 100 vòng/cm. Một vòng dây đơn bán kính 5,0 cm bao quanh ống dây, trục của ống dây và vòng dây trùng nhau. Dòng điện trong ống dây giảm từ 1,0 A đến 0,5 A với tốc độ không đổi trong khoảng thời gian 10 ms. Tính suất điện động trong vòng dây
Từ trường trong lòng ống dây là: \(B = 4\pi {.10^{ - 7}}nI\)
Tiết diện của ống dây là: \(S = \pi {r^2}\)
Từ thông gửi qua vòng dây đúng bằng từ thông gửi qua tiết diện của ống dây:
\(\Phi = NBS = 4\pi {.10^{ - 7}}nI.\pi {r^2} = 4{\pi ^2}{.10^{ - 7}}n{r^2}I\)
Độ lớn suất điện động tự cảm trong vòng dây là:
\(\begin{array}{l}\left| {{e_{tc}}} \right| = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = 4{\pi ^2}{.10^{ - 7}}n{r^2}\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}}\\ \Rightarrow \left| {{e_{tc}}} \right| = 4{\pi ^2}{.10^{ - 7}}{.100.10^2}.{\left( {{{25.10}^{ - 3}}} \right)^2}.\dfrac{{\left| {0,5 - 1} \right|}}{{{{10.10}^{ - 3}}}} \approx 1,{23.10^{ - 3}}\,\,\left( V \right) = 1,23\,\,\left( {mV} \right)\end{array}\)
Một thanh dẫn điện dài 1m, chuyển động trong từ trường đều có cảm ứng từ \(B{\rm{ }} = {\rm{ }}0,4T\) với vận tốc \(2m/s\) và làm với \(\overrightarrow B \) một góc \({30^0}\). Dùng dây có điện trở không đáng kể nối hai đầu thanh với một điện trở \(R = 2\Omega \) thành một mạch kín. Tính cường độ dòng điện qua điện trở?
Ta có:
+ Suất điện động cảm ứng trong thanh là: \(\left| {{e_C}} \right| = Blv\sin \theta = 0,4.1.2.sin{30^0} = 0,4V\)
=> Cường độ dòng điện trong mạch: \({I_c} = \dfrac{{{e_c}}}{R} = \dfrac{{0,4}}{2} = 0,2A\)
Ta có cường độ dòng điện trong mạch cũng chính là cường độ dòng điện qua điện trở và bằng \(0,2A\)
Một thanh dẫn điện dài \(80cm\), chuyển động vuông góc trong từ trường đều với vận tốc \(2m/s\). Biết cảm ứng từ có độ lớn \(B = 0,4T\). Tính suất điện động cảm ứng trong thanh.
Ta có:
Suất điện động cảm ứng trong thanh là: \(\left| {{e_C}} \right| = Blv\sin \theta = 0,4.0,8.2.sin{90^0} = 0,64V\)
Một thanh dẫn điện dài \(80cm\), chuyển động vuông góc trong từ trường đều với vận tốc \(2m/s\). Biết cảm ứng từ có độ lớn \(B = 0,4T\). Dùng dây dẫn có điện trở không đáng kể nối hai đầu thanh với một điện trở \(R = 0,8\Omega \) thành mạch kín thì cường độ dòng điện qua điện trở bằng bao nhiêu?
Ta có:
+ Suất điện động cảm ứng trong thanh là: \(\left| {{e_C}} \right| = Blv\sin \theta = 0,4.0,8.2.sin{90^0} = 0,64V\)
=> Cường độ dòng điện trong mạch: \({I_c} = \dfrac{{{e_c}}}{R} = \dfrac{{0,64}}{{0,8}} = 0,8A\)
Ta có cường độ dòng điện trong mạch cũng chính là cường độ dòng điện qua điện trở
Thanh kim loại AB dài 20cm kéo trượt đều trên hai thanh ray kim loại nằm ngang như hình vẽ:

Các dây nối với nhau bằng điện trở \(R = 3\Omega \), vận tốc của thanh AB là 12m/s. Hệ thống đặt trong từ trường đều có B = 0,4T, \(\overrightarrow B \) vuông góc với mạch điện. Suất điện động cảm ứng trong khung có giá trị là:
Suất điện động cảm ứng trong thanh: \(\left| {{e_C}} \right| = Blv\sin {90^0} = 0,4.0,2.12 = 0,96V\)
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh MN có chiều dài \(1m\) có điện trở \(R = 2,9\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ. \(B = 0,1T\).

Khi MN đứng yên, độ lớn lực từ tác dụng lên thanh MN khi đó có giá trị?
+ Khi MN đứng yên, thì trong mạch không có dòng điện cảm ứng , nên số chỉ của ampe kế là:
\(I = \dfrac{E}{{R + r}} = \dfrac{{1,5}}{{2,9 + 0,1}} = 0,5A\)
+ Lực từ tác dụng lên thanh MN khi này: \(F = BIl\sin {90^0} = 0,1.0,5.1 = 0,05N\)
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh MN có chiều dài \(1m\) có điện trở \(R = 2,9\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ. \(B = 0,1T\).

Khi MN di chuyển về phía bên phải với vận tốc \(v{\rm{ }} = {\rm{ }}3m/s\) sao cho hai đầu thanh MN luôn tiếp xúc hai thanh ray ? Tính độ lớn lực từ tác dụng lên thanh MN khi đó.
+ Dòng điện do nguồn tạo ra:
\(I = \dfrac{E}{{R + r}} = \dfrac{{1,5}}{{2,9 + 0,1}} = 0,5A\)
+ Khi thanh chuyển động về phía bên phải thì trong mạch có dòng điện cảm ứng có chiều từ M đến N và có độ lớn:
\({i_C} = \dfrac{{{e_C}}}{{R + r}} = \dfrac{{Blv}}{{R + r}} = \dfrac{{0,1.1.3}}{{2,9 + 0,1}} = 0,1A\)
Trong mạch có hai dòng điện là dòng do nguồn tạo ra và dòng cảm ứng do hiện tượng cảm ứng điện từ tạo ra, hai dòng này cùng chiều nên số chỉ của ampe kế là:
\({I_A} = I + {i_C} = 0,5 + 0,1 = 0,6A\)
+ Lực từ tác dụng lên thanh MN khi này là: \(F = B{I_A}l\sin {90^0} = 0,1.0,6.1 = 0,06N\)
Cho hệ thống như hình vẽ:
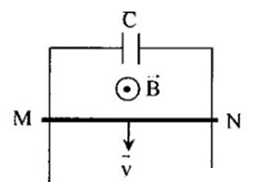
Thanh MN có chiều dài \(20cm\) chuyển động với vận tốc \(2m/s\) trong từ trường đều \(B{\rm{ }} = 0,04T\). Tụ điện có điện dung \(C = 2\mu F\). Độ lớn điện tích của tụ điện:
Khi thanh MN chuyển động thì thanh MN xem như nguồn điện có suất điện động có độ lớn: \({e_C} = Blv\sin {90^0} = 0,04.0,2.2 = 0,016V\)
Nguồn điện MN sẽ nạp điện cho tụ C nên điện tích của tụ C là:
\(q = C{e_C} = {2.10^{ - 6}}.0,016 = 3,{2.10^{ - 8}}(C) = 32\left( {nC} \right)\)
Thanh MN chiều dài \(l{\rm{ }} = {\rm{ }}20cm\) quay đều quanh trục qua M và vuông góc với thanh trong từ trường đều \(B = 0,04T\) làm thanh xuất hiện suất điện động cảm ứng \(e_C = {\rm{ }}0,4V\).
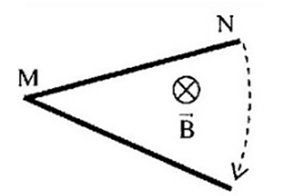
Tốc độ góc của thanh là:
Xét trong khoảng thời gian ∆t, thanh quét được diện tích:
\(\Delta S = \pi {l^2}\dfrac{{\Delta \varphi }}{{2\pi }} = \pi {l^2}\dfrac{{\omega \Delta t}}{{2\pi }} = \dfrac{{{l^2}\omega }}{2}\Delta t\)
Độ biến thiên từ thông : \(\Delta \Phi = B\Delta Sc{\rm{os}}\alpha = B\Delta S\) ( vì \(\cos \alpha = 1\))
+ Suất điện động cảm ứng:
\(\begin{array}{l}\left| {{e_C}} \right| = \dfrac{{\Delta \Phi }}{{\Delta t}} = \dfrac{{B\Delta S}}{{\Delta t}} = \dfrac{{B\dfrac{{{l^2}\omega }}{2}\Delta t}}{{\Delta t}} = \dfrac{{B{l^2}\omega }}{2}\\ \to \omega = \dfrac{{2e_C}}{{B{l^2}}} = \dfrac{{2.0,4}}{{0,04.{{(0,2)}^2}}} = 500(ra{\rm{d/s)}}\end{array}\)
Hai thanh kim loại song song thẳng đứng một đầu nối với tụ điện có điện dung \(C = 1\mu F\) . Một đoạn dây dẫn \(AB\) có độ dài \(l = 10cm\), khối lượng \(m = 15g\) tì vào hai thanh kim loại, tự do trượt không ma sát xuống dưới và luôn vuông góc với hai thanh kim loại trên. Hệ thống đặt trong từ trường đều vuông góc có \(B = 1T\) bỏ qua điện trở. Xác định gia tốc của thanh AB? Lấy \(g = 10m/{s^2}\)
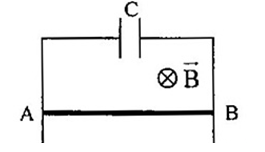
Ta có:
Thanh chịu tác dụng của trọng lực và lực từ
+ Theo định luật II – Newton, ta có: \(\overrightarrow P + \overrightarrow F = m\overrightarrow a \) (1)
Chọn chiều dương hướng xuống, chiếu (1) theo phương chuyển động động, ta được:
\(P - F = ma\) (2)
+ Ta có:
- Trọng lực \(P = mg\)
- Lực từ: \(F = BIl\)
Có cường độ dòng điện: \(I = \dfrac{{\Delta q}}{{\Delta t}} = \dfrac{{C\Delta {e_c}}}{{\Delta t}} = \dfrac{{CBl\Delta v}}{{\Delta t}} = CBla\)
Thay vào (2) ta được:
\(\begin{array}{l}mg - C{B^2}{l^2}a = ma\\ \Rightarrow a = \dfrac{{mg}}{{C{B^2}{l^2} + m}} = \dfrac{{{{15.10}^{ - 3}}.10}}{{{{10}^{ - 6}}{{.1}^2}.0,{1^2} + {{15.10}^{ - 3}}}} \approx 10m/{s^2}\end{array}\)
Ban đầu hai thanh kim loại song song thẳng đứng một đầu nối với tụ điện có điện dung \(C = 4\mu F\). Một đoạn dây dẫn AB có độ dài \(l = 10cm\), khối lượng \(m{\rm{ }} = {\rm{ }}20g\) tì vào hai thanh kim loại, tự do trượt không ma sát xuống dưới và luôn vuông góc với hai thanh kim loại trên. Hệ thống đặt trong từ trường đều vuông góc có \(B{\rm{ }} = {\rm{ }}1T\), bỏ qua điện trở.

Lúc sau, để thanh kim loại nghiêng so với phương ngang góc \({30^0}\), độ lớn và chiều của B như cũ. Đầu AB được được thả từ vị trí cách đầu dưới của thanh kim loại đoạn \(d{\rm{ }} = 5cm\) . Thời gian để AB bắt đầu rời khỏi thanh kim loại là:
Ta có, các lực tác dụng lên thanh gồm: Trọng lực \(\overrightarrow P \) và lực lorenxơ \(\overrightarrow f \)
+ Lực lorenxơ:
\(\begin{array}{l}f = BIl\\I = \dfrac{{\Delta q}}{{\Delta t}} = \dfrac{{C\Delta {e_c}}}{{\Delta t}} = CBl\dfrac{{\Delta v}}{{\Delta t}} = CBla'\end{array}\)
Khi hai thanh nghiêng góc \(\alpha = {30^0}\)
+ Theo định luật II-Newtơn, ta có:
Phương trình chuyển động của AB:
\(\begin{array}{l}P\sin \alpha - f\sin \alpha = ma'\\ \leftrightarrow mg\sin \alpha - C{B^2}{l^2}a'sin\alpha = ma'\\ \to a' = \dfrac{{mg\sin \alpha }}{{m + C{B^2}{l^2}\sin \alpha }}\\ = \dfrac{{{{20.10}^{ - 3}}.10.\sin {{30}^0}}}{{{{20.10}^{ - 3}} + {{4.10}^{ - 6}}{{.1}^2}.0,{1^2}.sin{{30}^0}}} \approx 5m/{s^2}\end{array}\)
Thời gian thanh AB rời khỏi thanh kim loại: \(d = \dfrac{1}{2}a'{t^2} \to t = \sqrt {\dfrac{{2{\rm{d}}}}{{a'}}} = \sqrt {\dfrac{{2.0,05}}{5}} = 0,14{\rm{s}}\)

