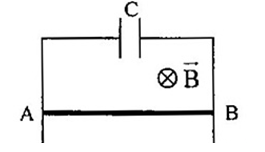
Hai thanh kim loại song song thẳng đứng một đầu nối với tụ điện có điện dung \(C = 1\mu F\) . Một đoạn dây dẫn \(AB\) có độ dài \(l = 10cm\), khối lượng \(m = 15g\) tì vào hai thanh kim loại, tự do trượt không ma sát xuống dưới và luôn vuông góc với hai thanh kim loại trên. Hệ thống đặt trong từ trường đều vuông góc có \(B = 1T\) bỏ qua điện trở. Xác định gia tốc của thanh AB? Lấy \(g = 10m/{s^2}\)

Một khung dây dẫn hình vuông cạnh a = 6 cm; đặt trong từ trường đều B = 4.10^-3 T, đường sức từ trường vuông góc với mặt phẳng khung dây. Cầm hai cạnh đối diện hình vuông kéo về hai phía để được hình chữ nhật có cạnh này dài gấp đôi cạnh kia trong khoảng thời gian 10^-6s. Độ lớn suất điện động cảm ứng xuất hiện trong khung là:

Một khung dây hình tròn bán kính 20 cm nằm toàn bộ trong một từ trường đều mà các đường sức từ vuông với mặt phẳng vòng dây. Trong thời gian t cảm ứng từ tăng từ 0,1 T đến 1,1 T thì trong khung dây có một suất điện động không đổi với độ lớn là 0,2 V. Thời gian t đó là

Một hình vuông cạnh 5cm được đặt trong từ trường đều B = 0,01 T. Đường sức từ vuông góc với mặt phẳng khung. Quay khung trong 10^-3 s để mặt phẳng khung dây song song với đường sức từ. Suất điện động trung bình xuất hiện trong khung là:

Một vòng dây dẫn tròn có diện tích \(0,4\,\,{m^2}\) đặt trong từ trường đều có cảm ứng từ \(B = 0,6\,\,T\), vecto cảm ứng từ vuông góc với mặt phẳng vòng dây. Nếu cảm ứng từ tăng đến \(1,4\,\,T\) trong thời gian \(0,25\,\,s\) thì độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là

Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh \(MN\) có chiều dài \(1m\) có điện trở \(R = 5\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ, độ lớn \(B{\rm{ }} = {\rm{ }}0,1T\)

Ampe kế chỉ bao nhiêu khi \(MN\) đứng yên?

Một khung dây cứng phẳng diện tích 25 cm² gồm 10 vòng dây, đặt trong từ trường đều, mặt phẳng khung vuông góc với các đường cảm ứng từ. Cảm ứng từ biến thiên theo thời gian như đồ thị hình vẽ. Tính suất điện động cảm ứng xuất hiện trong khung kể từ t = 0 đến t = 0,4 (s):

Một cuộn dây tròn gồm 1000 vòng dây, có diện tích 40 cm² đặt trong một từ trường đều có véc tơ cảm ứng từ vuông góc với mặt phẳng vòng dây. Trong thời gian ∆t = 0,02 giây, độ lớn của cảm ứng từ tăng đều từ 0 T đến 4.10^-3 T. Xác định độ lớn suất điện động cảm ứng xuất hiện trong cuộn dây.