Suất điện động tự cảm trong ống từ thời điểm \(0,05{\rm{ }}\left( s \right)\) về sau là:
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{2000^2}.\left( {{{5.10}^{ - 4}}} \right) = 8\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy từ thời điểm \(0,05s\) về sau thì cường độ dòng điện không đổi có giá trị bằng \(5A\)
=> Độ biến thiên cường độ dòng điện \(\Delta i = 0\)
=> Suất điện động tự cảm trong ống từ thời điểm \(0,05s\) về sau là: \({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 0V\)
Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{1000^2}.\left( {{{5.10}^{ - 4}}} \right) = 2\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy trong khoảng thời gian \(\Delta t = 0,05s\) thì cường độ dòng điện biến thiên từ \(0 \to 5A\)
=> Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
\({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 2\pi {.10^{ - 4}}\dfrac{{\left| {5 - 0} \right|}}{{0,05}} = 0,063V\)
Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{1000^2}.\left( {{{5.10}^{ - 4}}} \right) = 2\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy trong khoảng thời gian \(\Delta t = 0,05s\) thì cường độ dòng điện biến thiên từ \(0 \to 5A\)
=> Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
\({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 2\pi {.10^{ - 4}}\dfrac{{\left| {5 - 0} \right|}}{{0,05}} = 0,063V\)
Một diện tích \(S\) đặt trong từ trường đều có cảm ứng từ \(B\), góc giữa vectơ cảm ứng từ và vectơ pháp tuyến là \(\alpha \). Từ thông qua diện tích \(S\) được tính theo công thức:
Một diện tích \(S\) đặt trong từ trường đều có cảm ứng từ \(B\), góc giữa vectơ cảm ứng từ và vectơ pháp tuyến là \(\alpha \)
Từ thông qua diện tích \(S\) được tính theo công thức \(\Phi = BScos\alpha \)
Phát biểu nào sau đây là không đúng?
B, C , D - đúng
A – sai
Vì: Một khung dây dẫn hình chữ nhật, quay đều trong một từ trường đều quanh một trục đối xứng OO’ song song với các đường cảm ứng từ thì từ thông trong qua khung không biến thiên, trong khung không xuất hiện dòng điện cảm ứng.
Phát biểu nào sau đây là không đúng?
A, B, D – đúng
C – sai
Vì: Dòng điện cảm ứng có chiều sao cho từ trường do nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó. Khi từ thông tăng thì từ trường do dòng điện cảm ứng sinh ra ngược chiều với từ trường đã sinh ra nó, và ngược lại khi từ thông giảm thì từ trường do dòng điện cảm ứng sinh ra cùng chiều với từ trường đã sinh ra nó
Độ lớn của suất điện động cảm ứng trong một mạch kín được xác định theo công thức:
Độ lớn của suất điện động cảm ứng trong một mạch kín được xác định theo công thức \({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right|\)
Khung dây dẫn ABCD được đặt trong từ trường đều như hình sau. Coi rằng bên ngoài vùng MNPQ không có từ trường. Khung chuyển động dọc theo hai đường xx’, yy’. Trong khung sẽ xuất hiện dòng điện cảm ứng khi:
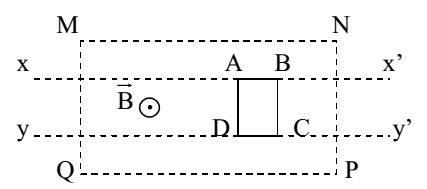
Ta có: Dòng điện xuất hiện khi có sự biến đổi từ thông qua mạch điện kín gọi là dòng điện cảm ứng
Khung dây dẫn ABCD được đặt trong từ trường đều .Coi rằng bên ngoài vùng MNPQ không có từ trường. Khung chuyển động dọc theo hai đường xx’, yy’. Trong khung sẽ xuất hiện dòng điện cảm ứng khi khung đang chuyển động ở ngoài vào trong vùng NMPQ vì khi đó từ thông qua khung biến thiên.
Từ thông \(\Phi \) qua một khung dây biến đổi, trong khoảng thời gian \(0,2{\rm{ }}\left( s \right)\) từ thông giảm từ \(1,2{\rm{ }}\left( {Wb} \right)\) xuống còn \(0,4{\rm{ }}\left( {Wb} \right)\). Suất điện động cảm ứng xuất hiện trong khung có độ lớn bằng:
Ta có, suất điện động cảm ứng xuất hiện trong khung:
\({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \dfrac{{\left| {0,4 - 1,2} \right|}}{{0,2}} = 4V\)
Một hình chữ nhật kích thước \(3{\rm{ }}\left( {cm} \right){\rm{ }}x{\rm{ }}4{\rm{ }}\left( {cm} \right)\) đặt trong từ trường đều có cảm ứng từ \(B = {5.10^{ - 4}}\left( T \right)\). Vectơ cảm ứng từ hợp với mặt phẳng một góc \({30^0}\). Từ thông qua hình chữ nhật đó là:
Ta có từ thông qua diện tích hình chữ nhật: \(\Phi = BScos\alpha \)
+ Diện tích \(S\) của hình chữ nhật: \(S = 0,03.0,04 = {1,2.10^{ - 3}}\left( {{m^2}} \right)\)
+\(\alpha = (\overrightarrow n ,\overrightarrow B ) = {90^0} - {30^0} = {60^0}\)
=> Từ thông qua hình chữ nhật: \(\Phi = BScos\alpha = {5.10^{ - 4}}{.1,2.10^{ - 3}}.cos{60^0} = {3.10^{ - 7}}\left( {{\rm{W}}b} \right)\)
Một hình vuông cạnh \(5cm\), đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4}}T\). Từ thông qua hình vuông đó bằng \({10^{ - 6}}{\rm{W}}b\). Góc hợp bởi vectơ cảm ứng từ và vectơ pháp tuyến với hình vuông đó là:
Ta có: từ thông qua diện tích hình chữ nhật: \(\Phi = BScos\alpha \)
+ Diện tích \(S\) của hình vuông: \(S = {0,05^2} = {2,5.10^{ - 3}}{m^2}\)
+ Từ thông qua hình vuông: \(\Phi = {10^{ - 6}}{\rm{W}}b\)
\(\begin{array}{l} \to cos\alpha = \dfrac{\Phi }{{BS}} = \dfrac{{{{10}^{ - 6}}}}{{{{4.10}^{ - 4}}{{.2,5.10}^{ - 3}}}} = 1\\ \to \alpha = {0^0}\end{array}\)
Một khung dây phẳng, diện tích \(20{\rm{ }}\left( {c{m^2}} \right)\), gồm \(10\) vòng dây đặt trong từ trường đều. Vectơ cảm ứng từ làm thành với mặt phẳng khung dây một góc \({30^0}\) và có độ lớn \(B{\rm{ }} = {\rm{ }}{2.10^{ - 4}}\left( T \right)\). Người ta làm cho từ trường giảm đều đến không trong khoảng thời gian \(0,01{\rm{ }}\left( s \right)\). Suất điện động cảm ứng xuất hiện trong khung dây trong khoảng thời gian từ trường biến đổi là:
Ta có:
+ Góc \(\alpha = (\overrightarrow n ,\overrightarrow B ) = {90^0} - {30^0} = {60^0}\)
=> Từ thông ban đầu qua khung dây: \(\Phi = BScos\alpha = {2.10^{ - 4}}{.20.10^{ - 4}}.cos{60^0} = {2.10^{ - 7}}{\rm{W}}b\)
+ Suất điện động cảm ứng qua khung dây trong khoảng thời gian:
\({e_c} = N\dfrac{{\left| {\Delta \Phi } \right|}}{{\Delta t}} = 10.\dfrac{{\left| {0 - {{2.10}^{ - 7}}} \right|}}{{0,01}} = {2.10^{ - 4}}V = 0,2mV\)
Một khung dây tròn, đặt trong từ trường tăng dần đều như hình sau.
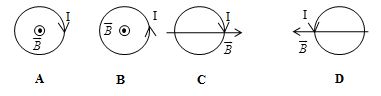
Dòng điện cảm ứng trong khung có chiều:
Ta có:
Định luật lenxơ về chiều dòng điện cảm ứng: Dòng điện cảm ứng có chiều sao cho từ trường mà nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
=> A – biểu diễn đúng chiều của dòng điện cảm ứng trong khung
Hình vẽ nào sau đây xác định sai chiều của dòng điện cảm ứng:
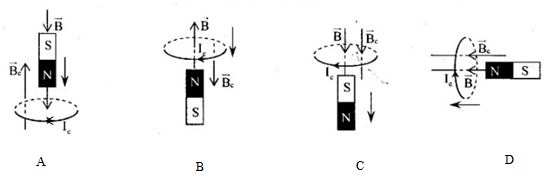
Định luật lenxơ về chiều dòng điện cảm ứng: Dòng điện cảm ứng có chiều sao cho từ trường mà nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
A- sai vì, theo quy tắc nắm bàn tay phải Ic phải có chiều như sau:
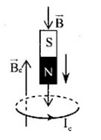
Phát biểu nào sau đây là đúng?
Quy tắc bàn tay phải để xác định chiều của suất điện động trong thanh:
Đặt bàn tay phải hứng các đường sức từ, ngón tay cái choãi ra \({90^0}\) hướng theo chiều chuyển động của đoạn dây, khi đó đoạn dây dẫn đóng vai trò như một nguồn điện, chiều từ cổ tay đến các ngón tay chỉ chiều từ cực âm sang cực dương của nguồn điện đó.
Máy phát điện hoạt động theo nguyên tắc dựa trên:
Máy phát điện hoạt động theo nguyên tắc dựa trên hiện tượng cảm ứng điện từ
Một thanh dây dẫn dài \(20{\rm{ }}\left( {cm} \right)\) chuyển động tịnh tiến trong từ trường đều có \(B{\rm{ }} = {5.10^{ - 4}}\left( T \right)\). Vectơ vận tốc của thanh vuông góc với thanh, vuông góc với vectơ cảm ứng từ và có độ lớn \(5{\rm{ }}\left( {m/s} \right)\). Suất điện động cảm ứng trong thanh là:
Suất điện động cảm ứng trong thanh: \(\left| {{e_c}} \right| = Bvl\sin \theta \) với \(\theta {\rm{ = }}\left( {\overrightarrow v ,\overrightarrow B } \right)\)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}B = {5.10^{ - 4}}T\\v = 5m/s\\l = 20cm = 0,2m\\\theta = {90^0}\end{array} \right.\)
=> \({e_c} = {5.10^{ - 4}}.5.0,2.sin{90^0} = {5.10^{ - 4}}V = 0,5mV\)
Một thanh dẫn điện dài \(20{\rm{ }}\left( {cm} \right)\) được nối hai đầu của nó với hai đầu của một mạch điện có điện trở \(0,5\Omega \). Cho thanh chuyển động tịnh tiến trong từ trường đều cảm ứng từ \(B = 0,08\left( T \right)\) với vận tốc \(7{\rm{ }}\left( {m/s} \right)\), vectơ vận tốc vuông góc với các đường sức từ và vuông góc với thanh, bỏ qua điện trở của thanh và các dây nối. Cường độ dòng điện trong mạch là:
+ Theo đề bài, ta có: \(\left\{ \begin{array}{l}B = 0,08T\\v = 7m/s\\l = 20cm = 0,2m\\\theta = {90^0}\end{array} \right.\)
=> \({e_c} = 0,08.7.0,2.cos{90^0} = 0,112V\)
+ Áp dụng định luật Ôm cho toàn mạch, ta có: \(I = \dfrac{{{e_c}}}{R} = \dfrac{{0,112}}{{0,5}} = 0,224A\)
Một thanh dẫn điện dài \(40{\rm{ }}\left( {cm} \right)\), chuyển động tịnh tiến trong từ trường đều, cảm ứng từ bằng \(0,4{\rm{ }}\left( T \right)\). Vectơ vận tốc của thanh vuông góc với thanh và hợp với các đường sức từ một góc \({30^0}\). Suất điện động giữa hai đầu thanh bằng \(0,2{\rm{ }}\left( V \right)\). Vận tốc của thanh là:
Suất điện động cảm ứng trong thanh: \(\left| {{e_c}} \right| = Bvl\sin \theta \) với \(\theta {\rm{ = }}\left( {\overrightarrow v ,\overrightarrow B } \right)\)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}B = 0,4T\\l = 40cm = 0,4m\\\theta = {30^0}\\{e_c} = 0,2V\end{array} \right.\)
=> \(v = \dfrac{{{e_c}}}{{Bl\sin \theta }} = \dfrac{{0,2}}{{0,4.0,4.\sin {{30}^0}}} = 2,5m/s\)
Dòng điện Fu-cô là:
Dòng điện cảm ứng được sinh ra ở trong khối vật dẫn khi vật dẫn chuyển động trong từ trường hay được đặt trong từ trường biến đổi theo thời gian là dòng điện Fu-cô

