Phát biểu nào sau đây là không đúng?
A, B, C - đúng
D- sai vì: Dòng điện cảm ứng được sinh ra ở trong khối vật dẫn khi vật dẫn chuyển động trong từ trường hay được đặt trong từ trường biến đổi theo thời gian là dòng điện Fu-cô
Muốn làm giảm hao phí do tỏa nhiệt của dòng điện Fu-cô gây trên khối kim loại, người ta thường dùng:
Muốn làm giảm hao phí do tỏa nhiệt của dòng điện Fu-cô gây trên khối kim loại, người ta thường chia khối kim loại thành nhiều lá kim loại mỏng ghép cách điện với nhau
Khi sử dụng điện, dòng điện Fucô sẽ xuất hiện trong:
Khi sử dụng điện dòng điện Fucô sẽ xuất hiện trong lõi sắt của quạt điện.
Phát biểu nào sau đây là không đúng?
B – sai vì: Sau khi siêu điện hoạt động, ta thấy nước trong siêu nóng lên. Sự nóng lên của nước chủ yếu là do dây dẫn trong siêu điện có dòng điện chạy qua, toả nhiệt theo định luật Jun – Lenxơ.
Phát biểu nào sau đây là không đúng?
D – sai vì: Suất điện động tự cảm là trường hợp đặc biệt của suất điện động cảm ứng.
Biểu thức tính suất điện động tự cảm là:
Suất điện động được sinh ra do hiện tượng tự cảm gọi là suất điện động tự cảm
\({e_{tc}} = - L\dfrac{{\Delta i}}{{\Delta t}}\)
Trong đó:
+ \({e_{tc}}\): suất điện động tự cảm
+ L: hệ số tự cảm
+ ∆i: Độ biến thiên cường độ dòng điện (A)
+ ∆t: Thời gian biến thiên cường độ dòng điện (s)
+ \(\dfrac{{\Delta i}}{{\Delta t}}\) : tốc độ biến thiên cường độ dòng điện (A/s)
Dấu “-“ giống như công thức tính suất điện động cảm ứng theo định luật Faraday chỉ chiều dòng điện cảm ứng tuân theo định luật Lenxơ
Một ống dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,1{\rm{ }}\left( H \right)\), cường độ dòng điện qua ống dây giảm đều đặn từ \(2{\rm{ }}\left( A \right)\) về \(0\) trong khoảng thời gian là \(4{\rm{ }}\left( s \right)\). Suất điện động tự cảm xuất hiện trong ống trong khoảng thời gian đó là:
Suất điện động tự cảm xuất hiện trong ống trong khoảng thời gian \(4s\) đó là:
\({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 0,1\dfrac{{\left| {0 - 2} \right|}}{4} = 0,05V\)
Một ống dây dài \(50{\rm{ }}\left( {cm} \right)\), diện tích tiết diện ngang của ống là \(10{\rm{ }}\left( {c{m^2}} \right)\) gồm \(1000\) vòng dây. Hệ số tự cảm của ống dây là:
Ta có: hệ số tự cảm của một ống dây dài đặt trong không khí:
\(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{l}S\)
Trong đó:
+ \(n\): số vòng dây trên một đơn vị chiều dài của ống \((n = \dfrac{N}{l})\)
+ \(V\) : thể tích của ống \((V = lS)\)
+\(S\): tiết diện của ống dây \(\left( {{m^2}} \right)\)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}N = 1000\\l = 50cm = 0,5m\\S = 10c{m^2} = {10^{ - 3}}{m^2}\end{array} \right.\)
=> Hệ số tự cảm của ống dây:
\(L = 4\pi {.10^{ - 7}}\dfrac{{{{1000}^2}}}{{0,5}}{.10^{ - 3}} = 8\pi {.10^{ - 4}}H = 2,513mH\)
Một ống dây được quấn với mật độ \(1000\) vòng/mét. Ống dây có thể tích \(500{\rm{ }}\left( {c{m^3}} \right)\). Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc, dòng điện trong ống biến đổi theo thời gian như hình dưới đây.
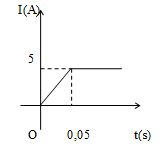
Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{1000^2}.\left( {{{5.10}^{ - 4}}} \right) = 2\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy trong khoảng thời gian \(\Delta t = 0,05s\) thì cường độ dòng điện biến thiên từ \(0 \to 5A\)
=> Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
\({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 2\pi {.10^{ - 4}}\dfrac{{\left| {5 - 0} \right|}}{{0,05}} = 0,063V\)
Một ống dây được quấn với mật độ \(1000\) vòng/mét. Ống dây có thể tích \(500{\rm{ }}\left( {c{m^3}} \right)\). Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc, dòng điện trong ống biến đổi theo thời gian như hình dưới đây.

Suất điện động tự cảm trong ống từ thời điểm \(0,05{\rm{ }}\left( s \right)\) về sau là:
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{2000^2}.\left( {{{5.10}^{ - 4}}} \right) = 8\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy từ thời điểm \(0,05s\) về sau thì cường độ dòng điện không đổi có giá trị bằng \(5A\)
=> Độ biến thiên cường độ dòng điện \(\Delta i = 0\)
=> Suất điện động tự cảm trong ống từ thời điểm \(0,05s\) về sau là: \({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 0V\)
Phát biểu nào sau đây là đúng?
A, B, C – sai
D – đúng
Vì: Khi có dòng điện chạy qua ống dây thì trong ống dây tồn tại một năng lượng dưới dạng năng lượng từ trường.
Năng lượng điện trường tồn tại trong tụ điện khi được tích điện.
Năng lượng từ trường tồn tại trong cuộn cảm
Năng lượng từ trường trong cuộn dây khi có dòng điện chạy qua được xác định theo công thức:
Năng lượng từ trường trong cuộn dây khi có dòng điện chạy qua được xác định theo công thức\(W = \dfrac{1}{2}L{I^2}\)
Một ống dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,01{\rm{ }}\left( H \right)\), có dòng điện \(I{\rm{ }} = {\rm{ }}5{\rm{ }}\left( A \right)\) chạy trong ống dây. Năng lượng từ trường trong ống dây là:
Năng lượng từ trường trong ống dây: \({\rm{W}} = \dfrac{1}{2}L{I^2} = \dfrac{1}{2}{.0,01.5^2} = 0,125J\)
Một ống dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,01{\rm{ }}\left( H \right)\). Khi có dòng điện chạy qua ống, ống dây có năng lượng \(0,08{\rm{ }}\left( J \right)\). Cường độ dòng điện trong ống dây bằng:
Ta có năng lượng từ trường trong ống dây: \({\rm{W}} = \dfrac{1}{2}L{I^2}\)
=> Cường độ dòng điện: \(I = \sqrt {\dfrac{{2W}}{L}} = \sqrt {\dfrac{{2.0,08}}{{0,01}}} = 4A\)
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh \(MN\) có chiều dài \(1m\) có điện trở \(R = 5\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ, độ lớn \(B{\rm{ }} = {\rm{ }}0,1T\)
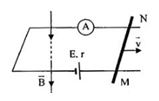
Ampe kế chỉ bao nhiêu khi \(MN\) đứng yên?
Khi \(MN\) đứng yên, thì trong mạch không có dòng điện cảm ứng , nên số chỉ của ampe kế là:
\(I = \dfrac{E}{{R + r}} = \dfrac{{1,5}}{{5 + 0,1}} = 0,29A\)
Một khung dây phẳng có diện tích \(25cm^2\), gồm \(10\) vòng dây đặt trong từ trương đều, mặt phẳng vòng dây vuông góc với các đường sức từ. Hình bên là đồ thị biểu diễn sự phụ thuộc của cảm ứng từ \(B\) vào thời gian \(t\). Độ lớn của suất điện động cảm ứng xuất hiện trong khung từ thời điểm \(t_1= 0\) đến thời điểm \(t_2= 0,5s\) là
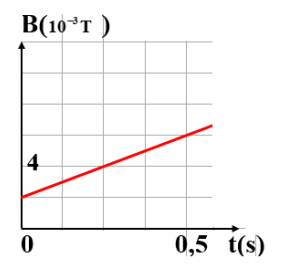
Suất điện động cảm ứng xuất hiện trong thời gian từ t1 = 0 đến t2 = 0,5s là
\(e = - \dfrac{{\Delta \phi }}{{\Delta t}} = - \dfrac{{N({B_2} - {B_1})S\cos 0}}{{{t_2} - {t_1}}} = - \dfrac{{10.({{6.10}^{ - 3}} - {{2.10}^{ - 3}}){{.25.10}^{ - 4}}}}{{0,5}} = {2.10^{ - 4}}V\)

