Câu hỏi:
2 năm trước
Một ống dây được quấn với mật độ \(1000\) vòng/mét. Ống dây có thể tích \(500{\rm{ }}\left( {c{m^3}} \right)\). Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc, dòng điện trong ống biến đổi theo thời gian như hình dưới đây.
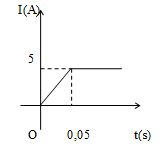
Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
+ Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{1000^2}.\left( {{{5.10}^{ - 4}}} \right) = 2\pi {.10^{ - 4}}H\)
+ Từ đồ thị ta thấy trong khoảng thời gian \(\Delta t = 0,05s\) thì cường độ dòng điện biến thiên từ \(0 \to 5A\)
=> Suất điện động tự cảm trong ống từ sau khi đóng công tắc đến thời điểm \(0,05{\rm{ }}\left( s \right)\) là:
\({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 2\pi {.10^{ - 4}}\dfrac{{\left| {5 - 0} \right|}}{{0,05}} = 0,063V\)
Hướng dẫn giải:
+ Sử dụng biểu thức xác định hệ số tự cảm của một ống dây dài đặt trong không khí:
\(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{l}S\)
+ Đọc đồ thị \(\left( {i - t} \right)\)
+ Áp dụng công thức tính độ lớn của suất điện động tự cảm là \({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}}\)
Câu hỏi khác
- Bài tập suất điện động cảm ứng trong một đoạn dây dẫn chuyển động lý 11 có lời giải
- Bài tập từ thông - Hiện tượng cảm ứng điện từ lý 11 có lời giải
- Bài tập ôn tập chương 5: Cảm ứng điện từ lý 11 có lời giải
- Bài tập hiện tượng tự cảm - Năng lượng từ trường lý 11 có lời giải
- Bài tập dòng điện fucô lý 11 có lời giải
