Một cuộn cảm có độ tự cảm \(0,2 H\). Khi cường độ dòng điện trong cuộn cảm giảm đều từ \(I\) xuống \(0\) trong khoảng thời gian \(0,05 s\) thì suất điện động tự cảm xuất hiện trong cuộn cảm có độ lớn là \(8 V\). Giá trị của \(I\) là
Ta có: \({e_{tc}} = - L\dfrac{{\Delta i}}{{\Delta t}}\)
\( \to \left| {{e_{tc}}} \right| = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} \leftrightarrow 8 = 0,2\dfrac{{I - 0}}{{0,05}} \to I = 2A\)
Một ống dây dài \(50\,\,cm\) tiết diện ngang là \(10\,\,c{m^2}\) gồm \(100\) vòng. Hệ số tự cảm của ống dây là
Hệ số tự cảm của ống dây là:
\(L = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}S}}{{\rm{l}}} = 4\pi {.10^{ - 7}}.\dfrac{{{{100}^2}.\left( {{{10.10}^{ - 4}}} \right)}}{{0,5}} \approx {25.10^{ - 6}}\,\,\left( H \right) = 25\,\,\left( {\mu H} \right)\)
Một dòng điện trong ống dây phụ thuộc vào thời gian theo biểu thức \(I = 0,4\left( {5 - t} \right);\,\,I\) tính bằng ampe, \(t\) tính bằng giây. Ống dây có hệ số tự cảm \(L = 0,005\,\,H\). Độ lớn suất điện động tự cảm trong ống dây là
Cường độ dòng điện tại các thời điểm \({t_1};\,\,{t_2}\) là:
\(\begin{array}{l}\left\{ \begin{array}{l}{I_1} = 0,4.\left( {5 - {t_1}} \right)\\{I_2} = 0,4.\left( {5 - {t_2}} \right)\end{array} \right.\\ \Rightarrow \Delta i = {I_2} - {I_1} = 0,4.\left( {5 - {t_2}} \right) = 0,4.\left( {5 - {t_1}} \right) = 0,4.\left( {{t_1} - {t_2}} \right) = - 0,4.\Delta t\end{array}\)
Độ lớn suất điện động tự cảm trong ống dây là:
\({e_c} = \left| { - L\frac{{\Delta i}}{{\Delta t}}} \right| = L.\frac{{\left| {\Delta i} \right|}}{{\Delta t}} = 0,005.\frac{{\left| { - 0,4\Delta t} \right|}}{{\Delta t}} = 0,002\,\,\left( V \right)\)
Độ tự cảm của một ống dây không có lõi sắt (có chiều dài ống dây là \(\ell \) gồm N vòng tiết diện một vòng dây là S) là:
Độ tự cảm của một ống dây không có lõi sắt (có chiều dài ống dây là \(\ell \) gồm N vòng tiết diện một vòng dây là S) là: \(L = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{\ell }S\)
Biểu thức tính hệ số tự cảm của ống dây dài là:
Biểu thức tính hệ số tự cảm của ống dây dài là: \(L = 4\pi {.10^{ - 7}}.{n^2}.V\) với \(n = \dfrac{N}{\ell }\)
Một ống dây có hệ số tự cảm là L. Cho dòng điện qua ống dây biến thiên một lượng \(\Delta I\) trong thời gian \(\Delta t\) thì suất điện động tự cảm xuất hiện trong ống dây là
Suất điện động tự cảm được xác định bởi biểu thức: \({e_{tc}} = - L\dfrac{{\Delta i}}{{\Delta t}}\)
Chọn phát biểu sai.
Suất điện động tự cảm có giá trị lớn khi cường độ dòng điện chạy qua mạch có giá trị
Ta có: Suất điện động tự cảm: \({e_{tc}} = - L\dfrac{{\Delta i}}{{\Delta t}}\)
=> Suất điện động tự cảm có giá trị lớn khi:
+ L - lớn: Độ tự cảm của ống dây lớn
+ \(\dfrac{{\Delta i}}{{\Delta t}}\) lớn hay chính là độ tăng/ giảm cường độ dòng điện trong một khoảng thời gian nhanh (hay nói cách khác là biến đổi nhanh)
=> Ta suy ra: Suất điện động tự cảm có giá trị lớn khi cường độ dòng điện I chạy qua mạch có giá trị thay đổi nhanh không phụ thuộc vào độ lớn của I.
Điều nào sau đây không đúng khi nói về hệ số tự cảm của ống dây?
Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V\)
A, B, D - đúng
C – sai vì: Hệ số tự cảm của ống dây phụ thuộc vào chiều dài của ống dây
Độ tự cảm của một ống dây không phụ thuộc
Ta có, độ tự cảm của ống dây:
\(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{\ell }S\)
=> Độ tự cảm của một ống dây không phụ thuộc cường độ dòng điện \(I\) qua ống dây.
Biết rằng cứ trong thời gian \({10^{ - 3}}s\) thì cường độ dòng điện trong mạch giảm đều một lượng là 1 A và suất điện động tự cảm trong cuộn dây là 11,2 V. Độ tự cảm của cuộn dây bằng:
Ta có, suất điện động tự cảm trong cuộn dây:
\(\begin{array}{l}\left| {{e_{tc}}} \right| = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}}\\ \to L = \dfrac{{\left| {{e_{tc}}} \right|\Delta t}}{{\left| {\Delta i} \right|}} = \dfrac{{11,{{2.10}^{ - 3}}}}{1} = 0,0112(H)\end{array}\)
Khi có dòng điện 1 A chạy qua ống dây có 10 vòng thì từ thông qua ống là 0,8 Wb. Hệ số tự cảm của ống dây là
Ta có, từ thông qua ống: \(\Phi = LI\)
=> Hệ số tự cảm của ống dây là: \( \Rightarrow L = \dfrac{\Phi }{I} = \dfrac{{0,8}}{1} = 0,8\,H\)
Một cuộn cảm có độ tự cảm \(0,1\,\,\left( H \right)\), trong đó có dòng điện biến thiên đều \(200\,\,\left( {A/s} \right)\) thì suất điện động tự cảm xuất hiện có độ lớn:
Độ lớn của suất điện động tự cảm trong cuộn cảm là:
\(\left| {{e_{tc}}} \right| = L\frac{{\Delta i}}{{\Delta t}} = 0,1.200 = 20\,\,\left( V \right)\)
Một ống dây dài \(50{\rm{ }}cm\), diện tích tiết diện ngang của ống dây là \(10c{m^2}\) gồm \(1000\) vòng dây. Hệ số tự cảm của ống dây là:
- Hệ số tự cảm của ống dây được tính theo công thức: \(L = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{\ell }S\)
Với: + N là số vòng của ống dây.
+ \(\ell \): chiều dài ống dây.
+ S diện tích mặt cắt ngang của ống dây.
- Vậy: \(L = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{\ell }S = 4\pi {.10^{ - 7}}\dfrac{{{{1000}^2}}}{{0,5}}{1.10^{ - 3}} = 2,{51.10^{ - 3}}H = 2,51\,mH\)
Cho dòng điện \(I{\rm{ }} = {\rm{ }}5A\) chạy trong ống dây có chiều dài \(1m\). Năng lượng từ trường bên trong ống dây là \(0,4J\). Nếu ống dây gồm 1200 vòng dây thì bán kính của ống dây là bao nhiêu?
Ta có:
+ Năng lượng từ trường bên trong ống dây:
\(\begin{array}{l}{\rm{W}} = \dfrac{1}{2}L{i^2}\\ \to L = \dfrac{{2{\rm{W}}}}{{{i^2}}} = \dfrac{{2.0,4}}{{{5^2}}} = 0,032H\end{array}\)
+ Hệ số tự cảm:
\(\begin{array}{l}L = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{l}S = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{l}\pi {R^2}\\ \to R = \sqrt {\dfrac{{l.L}}{{4{\pi ^2}{{.10}^{ - 7}}.{N^2}}}} = \sqrt {\dfrac{{1.0,032}}{{4{\pi ^2}{{.10}^{ - 7}}{{.1200}^2}}}} = 0,075m = 7,5cm\end{array}\)
Một ống dây dài được cuốn với mật độ \(2000\) vòng/mét. Ống dây có thể tích \(500c{m^3}\) . Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc dòng điện trong ống dây biến đổi theo thời gian (đồ thị). Lúc đóng công tắc ứng với thời điểm t = 0. Suất điện động tự cảm trong ống dây sau khi đóng công tắc với thời điểm \(t{\rm{ }} = {\rm{ }}0,05s\) có giá trị:
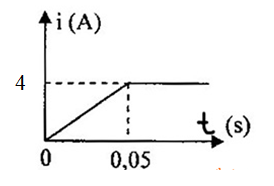
Ta có:
+ Độ tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}{2000^2}.({500.10^{ - 6}}) = 2,{5.10^{ - 3}}\)
+Trong khoảng thời gian từ \(t{\rm{ }} = {\rm{ }}0\) đến cường độ dòng điện tăng từ \(0A\) đến \(4A\)
Suất điện động tự cảm trong ống dây trong khoảng thời gian này:
\(\left| {{e_{tc}}} \right| = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = 2,{5.10^{ - 3}}\dfrac{{\left| {4 - 0} \right|}}{{0,05}} = 0,2V\)
Một ống dây dài được cuốn với mật độ \(2000\) vòng/mét. Ống dây có thể tích \(500c{m^3}\) . Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc dòng điện trong ống dây biến đổi theo thời gian (đồ thị). Lúc đóng công tắc ứng với thời điểm t = 0. Suất điện động tự cảm trong ống dây từ thời điểm \(t{\rm{ }} = {\rm{ }}0,05s\) về sau có giá trị là?
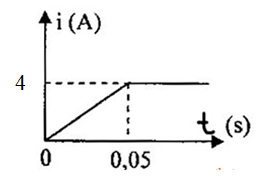
Từ đồ thị, ta thấy: Từ sau thời điểm \(t{\rm{ }} = {\rm{ }}0,05s\) cường độ dòng điện không thay đổi\( \leftrightarrow \Delta i = 0 \to {e_{tc}} = 0V\)
Cho mạch điện như hình vẽ, \(L = 1mH;E = 12V;r = 0\), điện trở của biến trở là \(6\Omega \). Điều chỉnh biến trở để trong \(0,01s\) điện trở của biến trở giảm còn \(3\Omega \).
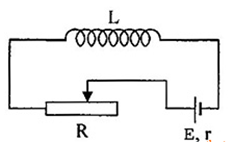
Suất điện động tự cảm xuất hiện trong ống dây trong khoảng thời gian trên có giá trị:
Ta có, khi R thay đổi thì dòng điện trong mạch cũng thay đổi nên suất hiện suất điện động tự cảm:
\(\left| {{e_{tc}}} \right| = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right|\)
trong đó: \({i_1} = \dfrac{E}{{{R_1} + r}} = \dfrac{E}{{{R_1}}};{i_2} = \dfrac{E}{{{R_2} + r}} = \dfrac{E}{{{R_2}}}\)
\( \to \left| {{e_{tc}}} \right| = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = L\left| {\left( {\dfrac{E}{{{R_1}}} - \dfrac{E}{{{R_2}}}} \right)} \right|\dfrac{1}{{\Delta t}} = {10^{ - 3}}.\left| {\left( {\dfrac{{12}}{6} - \dfrac{{12}}{3}} \right)} \right|\dfrac{1}{{0,01}} = 0,2V\)
Một ống dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,01{\rm{ }}H\) , có dòng điện \(I{\rm{ }} = {\rm{ }}5{\rm{ }}A\) chạy ống dây. Năng lượng từ trường trong ống dây là
Năng lượng từ trường trong ống dây: \({\rm{W}} = \dfrac{{L{I^2}}}{2} = \dfrac{{0,{{01.5}^2}}}{2} = 0,125\,\,J.\)
Một ống dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,01{\rm{ }}H\). Khi có dòng điện chạy qua ống , ống dây có năng lượng \(0,08{\rm{ }}J\). Cường độ dòng điện trong ống dây bằng:
Ta có:
Năng lượng từ trường trong ống dây: \({\rm{W}} = \dfrac{1}{2}L{I^2}\)
=> Cường độ dòng điện trong ống dây: \(I = \sqrt {\dfrac{{2W}}{L}} = \sqrt {\dfrac{{2.0,08}}{{0,01}}} = 4\,\,A\)
Một ống dây dài \(40{\rm{ }}cm\) có tất cả \(800\) vòng dây. Diện tích tiết diện ngang của ống dây bằng \(10c{m^2}\). Ống dây được nối với một nguồn điện, cường độ dòng điện qua ống dây tăng từ \(0A\) đến \(4{\rm{ }}A\). Nguồn điện đã cung cấp cho ống dây một năng lượng là:
+ Độ tự cảm của ống dây:
\(L = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{\ell }S = 4\pi {.10^{ - 7}}.\dfrac{{{{800}^2}}}{{0,4}}{1.10^{ - 3}} = 2,{01.10^{ - 3}}\,\,H.\)
+ Năng lượng của ống dây được cung cấp:
\({\rm{W}} = \dfrac{1}{2}L{I^2} = \dfrac{1}{2}.2,{01.10^{ - 3}}{.4^2} = 0,016\,\,J.\)

