Câu hỏi:
2 năm trước
Cho mạch điện như hình vẽ, \(L = 1mH;E = 12V;r = 0\), điện trở của biến trở là \(6\Omega \). Điều chỉnh biến trở để trong \(0,01s\) điện trở của biến trở giảm còn \(3\Omega \).
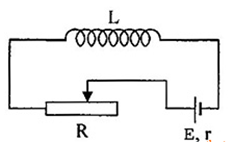
Suất điện động tự cảm xuất hiện trong ống dây trong khoảng thời gian trên có giá trị:
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có, khi R thay đổi thì dòng điện trong mạch cũng thay đổi nên suất hiện suất điện động tự cảm:
\(\left| {{e_{tc}}} \right| = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right|\)
trong đó: \({i_1} = \dfrac{E}{{{R_1} + r}} = \dfrac{E}{{{R_1}}};{i_2} = \dfrac{E}{{{R_2} + r}} = \dfrac{E}{{{R_2}}}\)
\( \to \left| {{e_{tc}}} \right| = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = L\left| {\left( {\dfrac{E}{{{R_1}}} - \dfrac{E}{{{R_2}}}} \right)} \right|\dfrac{1}{{\Delta t}} = {10^{ - 3}}.\left| {\left( {\dfrac{{12}}{6} - \dfrac{{12}}{3}} \right)} \right|\dfrac{1}{{0,01}} = 0,2V\)
Hướng dẫn giải:
Vận dụng biểu thức xác định suất điện động cảm ứng: \(\left| {{e_{tc}}} \right| = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right|\)
Câu hỏi khác
- Bài tập suất điện động cảm ứng trong một đoạn dây dẫn chuyển động lý 11 có lời giải
- Bài tập từ thông - Hiện tượng cảm ứng điện từ lý 11 có lời giải
- Bài tập ôn tập chương 5: Cảm ứng điện từ lý 11 có lời giải
- Bài tập hiện tượng tự cảm - Năng lượng từ trường lý 11 có lời giải
- Bài tập dòng điện fucô lý 11 có lời giải
