Một ống dây có hệ số tự cảm L = 0,1 H, cường độ dòng điện qua ống dây giảm đều đặn từ 2 A về 0 trong khoảng thời gian là 4 s. Suất điện động tự cảm xuất hiện trong ống trong khoảng thời gian đó là:
Độ lớn suất điện động tự cảm trong ống dây là:
\(\left| {{e_{tc}}} \right| = L.\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = 0,1.\dfrac{{\left| {0 - 2} \right|}}{4} = 0,05\,\,\left( V \right)\)
Một ống dây dài 50 cm có 2500 vòng dây. Đường kính của ống bằng 2 cm. Cho một dòng điện biến đổi đều theo thời gian chạy qua ống dây. Sau thời gian 0,01 s dòng điện tăng từ 0 đến 1,5 A. Tính suất điện động tự cảm trong ống dây.
Độ tự cảm của ống dây:
\(L = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}}}{l}.S = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}}}{l}.\dfrac{{\pi {d^2}}}{4} = 4\pi {.10^{ - 7}}.\dfrac{{{{2500}^2}}}{{0,5}}.\dfrac{{\pi .0,{{02}^2}}}{4} = 4,{9.10^{ - 3}}H\)
Độ lớn suất điện động tự cảm: \(\left| {{e_{tc}}} \right| = L.\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = 4,{9.10^{ - 3}}.\left| {\dfrac{{1,5 - 0}}{{0,01}}} \right| = 0,74V\)
Một cuộn tự cảm có L = 50mH cùng mắc nối tiếp với một điện trở R = 20Ω, nối vào một nguồn điện có suất điện động 90V, có điện trở trong không đáng kể. Xác định tốc độ biến thiên của cường độ dòng điện I tại thời điểm ban đầu ứng với I = 0.
Ta có: \(e + {e_{tc}} = RI \Leftrightarrow e - L.\dfrac{{\Delta i}}{{\Delta t}} = RI \Rightarrow \dfrac{{\Delta i}}{{\Delta t}} = \dfrac{{e - RI}}{L}\)
Với: \(\left\{ \begin{array}{l}e = 90V\\L = 0,05H\\R = 20\Omega \\I = 0\end{array} \right. \Rightarrow \dfrac{{\Delta i}}{{\Delta t}} = \dfrac{{e - RI}}{L} = \dfrac{{90 - 20.0}}{{0,05}} = 1800A/s\)
Một ống dây dài 40cm, có tất cả 800 vòng dây, diện tích tiết diện ngang của ống dây bằng 10 cm2. Ống dây được nối với 1 nguồn điện có cường độ tăng từ 0 → 4A. Nếu suất điện động tự cảm của ống dây có độ lớn là 1,2V, hãy xác định thời gian mà dòng điện đã biến thiên.
Độ tự cảm của ống dây:
\(L = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}}}{l}.S = 4\pi {.10^{ - 7}}.\dfrac{{{{800}^2}}}{{0,4}}{.10.10^{ - 4}} = {2.10^{ - 3}}H\)
Suất điện động tự cảm sinh ra do có sự biến thiên của dòng điện trong ống dây:
\(\left| {{e_{tc}}} \right| = L.\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = L.\left| {\dfrac{{{i_2} - {i_1}}}{{\Delta t}}} \right| \Rightarrow \Delta t = L.\left| {\dfrac{{{i_2} - {i_1}}}{{{e_{tc}}}}} \right| = {2.10^{ - 3}}.\left| {\dfrac{{4 - 0}}{{1,2}}} \right| = 6,{7.10^{ - 3}}s = 6,7ms\)
Tính độ tự cảm của mỗi ống dây hình trụ có chiều dài 0,5 m gồm 1000 vòng dây, mỗi vòng dây có đường kính 20 cm.
Độ tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}}}{l}.S\)
Theo đề bài ta có:
+ Số vòng dây : N = 1000 vòng
+ Chiều dài ống dây : l = 0,5m
+ Diện tích mỗi vòng dây : \(S = \pi .\dfrac{{{d^2}}}{4} = \pi .\dfrac{{0,{2^2}}}{4} = 0,01\pi \,\,\left( {{m^2}} \right)\)
Độ tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}.\dfrac{{{N^2}}}{l}.S = 4\pi {.10^{ - 7}}.\dfrac{{{{1000}^2}}}{{0,5}}.0,01\pi = 0,079H\)
Dòng điện chạy qua cuộn cảm có cường độ biến đổi theo thời gian như đồ thị hình bên. Gọi suất điện động tự cảm trong khoảng thời gian 0s đến 1s là e1, từ 1s đến 3s là e2 thì
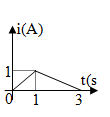
Công thức tính suất điện động cảm ứng :
\({e_1} = - \frac{{\Delta {\Phi _1}}}{{\Delta t}} = - L\frac{{\Delta {i_1}}}{{\Delta t}} = - L.\frac{1}{1}(V)\)
Công thức tính suất điện động cảm ứng :
\({e_2} = - \frac{{\Delta {\Phi _2}}}{{\Delta t}} = - L\frac{{\Delta {i_2}}}{{\Delta t}} = - L.\frac{1}{2}(V) = \frac{{{e_1}}}{2}\)
Một cuộn cảm có độ tự cảm 0,2 H. Khi cường độ dòng điện trong cuộn cảm giảm đều từ I xuống 0 trong khoảng thời gian 0,05 s thì suất điện động tự cảm xuất hiện trong cuộn cảm có độ lớn là 8 V. Giá trị của I là
Độ lớn suất điện động tự cảm:
\(\left| {{e_{tc}}} \right| = L.\left| {\frac{{\Delta i}}{{\Delta t}}} \right| \Leftrightarrow \left| {{e_{tc}}} \right| = L.\left| {\frac{{I - 0}}{{0,05}}} \right|\)
\( \Leftrightarrow 8 = 0,2.\frac{I}{{0,05}} \Rightarrow I = 2A\)
Suất điện động tự cảm có giá trị lớn khi
Nhận xét: Suất điện động tự cảm có giá trị lớn khi \(\left( \frac{\Delta i}{\Delta t} \right)\) có giá trị lớn, khi dòng điện tăng nhanh.
Trong một mạch kín có độ tự cảm \(L = 2mH\). Nếu suất điện động tự cảm bằng \(0,25V\) thì tốc độ biến thiên của dòng điện bằng bao nhiêu?
Ta có:
Suất điện động tự cảm:
\(\begin{array}{l}\left| {{e_{tc}}} \right| = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}}\\ \to \dfrac{{\left| {\Delta i} \right|}}{{\Delta t}} = \dfrac{{\left| {{e_{tc}}} \right|}}{L} = \dfrac{{0,25}}{{{{2.10}^{ - 3}}}} = 125(A/s)\end{array}\)
Một ống dây có hệ số tự cảm L = 0,1 H, cường độ dòng điện qua ống dây giảm đều đặn từ 2 A về 0 trong khoảng thời gian 4 s. Suất điện động tự cảm xuất hiện trong ống trong khoảng thời gian đó là
Ta có:
\({e_{tc}} = L\left| {\dfrac{{\Delta i}}{{\Delta t}}} \right| = 0,1.\left| {\dfrac{{2 - 0}}{4}} \right| = 0,05\,\,V.\)
Vậy suất điện động tự cảm xuất hiện trong ống trong khoảng thời gian đó là 0,05V.
Trong mạch điện như hình vẽ, cuộn cảm L có điện trở bằng không. Lúc đầu đóng khóa K về vị trí a để nạp năng lượng cho cuộn cảm L, khi đó dòng điện qua L bằng \(2A\) . Chuyển K sang vị trí b, nhiệt lượng tỏa ra trong R là bao nhiêu? Biết cuộn dây có độ tự cảm \(L = 2mH\)
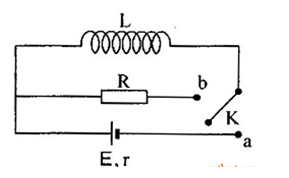
Ta có: Năng lượng cuộn cảm L tích trữ được: \({\rm{W}} = \dfrac{1}{2}L{i^2} = \dfrac{1}{2}{2.10^{ - 3}}{.2^2} = {4.10^{ - 3}}(J)\)
Khi chuyển khóa K sang vị trí b thì toàn bộ năng lượng tích trữ trên cuộn cảm L sẽ chuyển dang tỏa nhiệt hết trên R.
=> Nhiệt lượng tỏa ra trên R là \({4.10^{ - 3}}J\)
Trong một mạch kín, suất điện động tự cảm có giá trị lớn khi cường độ dòng điện
Ta có suất điện động tự cảm: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\)
\( \Rightarrow \) Suất điện động tự cảm có giá trị lớn khi cường độ dòng điện biến thiên nhanh.
Công thức tính suất điện động tự cảm là
Công thức tính suất điện động tự cảm: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\)
Cho mạch điện như hình vẽ.
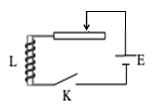
Hiện tượng tự cảm phát sinh khi mạch điện có hiện tượng nào sau đây:
Hiện tượng tự cảm là hiện tượng cảm ứng điện từ trong một mạch điện do chính sự biến đổi của dòng điện trong mạch đó gây ra
Cả ba trường hợp trên đều có sự biến đổi của dòng điện trong mạch
A- cường độ dòng điện từ 0 đến I
B- cường độ dòng điện từ I về 0
C- Khi di chuyển con chạy => điện trở thay đổi =>cường độ dòng điện cũng thay đổi
=>Hiện tượng tự cảm xuất hiện trong cả ba trường hợp
Cho mạch điện như hình vẽ. Chọn đáp án đúng. Khi đóng khóa K thì:
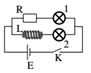
Khí đóng khóa K, đèn 1 sáng lên ngay còn đèn 2 sáng lên chậm hơn đèn 1.
* Giải thích: Khi đóng khóa K, dòng điện qua ống dây tăng lên đột ngột trong khoảng thời gian ngắn (cường độ dòng điện tăng từ 0 - I) làm cho từ trường qua ống dây tăng lên => từ thông qua cuộn dây tăng lên
Trong khoảng thời gian từ thông qua cuộn dây biến thiên sinh ra dòng điện cảm ứng theo định luật Lenxơ, dòng điện cảm ứng có chiều chống lại sự tăng của từ thông => nó làm giảm cường độ dòng điện qua đèn 2, làm đèn 2 sáng chậm hơn đèn 1.
Hệ số tự cảm của ống dây được xác định bởi biểu thức nào sau đây?
Hệ số tự cảm của ống dây được xác định bởi biểu thức: \(L = 4\pi {.10^{ - 7}}{n^2}V\)
Suất điện động tự cảm được xác định bởi biểu thức nào sau đây?
Suất điện động tự cảm được xác định bởi biểu thức: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\)
Đáp án nào sau đây là sai: Suất điện động tự cảm có giá trị lớn khi:
Ta có: Suất điện động tự cảm: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\)
=> Suất điện động tự cảm có giá trị lớn khi:
+ L - lớn: Độ tự cảm của ống dây lớn
+ ∆i lớn: Độ tăng/ giảm cường độ dòng điện nhanh
=> A, C, D - đúng
B- sai
Đáp án nào sau đây là sai: Hệ số tự cảm của ống dây:
A, B, D - đúng
C- sai vì: \(L = 4\pi {.10^{ - 7}}{n^2}V\)
Dòng điện trong cuộn tự cảm giảm từ 16A đến 0A trong 0,01s; suất điện động tự cảm trong đó có giá trị trung bình 64V; độ tự cảm có giá trị:
Ta có:
\(\left| {{e_{tc}}} \right| = L\frac{{\left| {\Delta i} \right|}}{{\Delta t}} \to L = \frac{{\left| {{e_{tc}}} \right|\Delta t}}{{\left| {\Delta i} \right|}} = \frac{{64.0,01}}{{16}} = 0,04(H)\)

