Cho hai điện tích điểm q1 = – q2 = 4 μC đặt tại hai điểm A, B trong không khí với AB = 5 cm. Cường độ điện trường tại M với MA = 3 cm, MB = 8 cm là

Ta có:
\(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon r_1^2}} = {9.10^9}.\frac{{\left| {{{4.10}^{ - 6}}} \right|}}{{0,{{03}^2}}} = {4.10^7}V/m\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon r_2^2}} = {9.10^9}.\frac{{\left| { - {{4.10}^{ - 6}}} \right|}}{{0,{{08}^2}}} = 0,{5625.10^7}V/m\end{array} \right.\)
\(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} > {E_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow E \uparrow \uparrow \overrightarrow {{E_1}} \\E = {E_1} - {E_2} = 34,{375.10^6}V/m\end{array} \right.\)
Cho hai điện tích q1 = 16 nC và q2 = – 36 nC đặt tại hai điểm A, B trong không khí với AB = 10 cm. Vị trí của điểm M mà tại đó cường độ điện trường bằng 0.
Ta có: q1, q2 trái dấu.
Cường độ điện trường tại M bằng 0 khi:
\(\left\{ \begin{array}{l}\overrightarrow {{E_{1M}}} \uparrow \downarrow \overrightarrow {{E_{2M}}} \\{E_{1M}} = {E_{2M}}\end{array} \right.\)
=> M nằm trên đường thẳng AB, nằm ngoài đoạn AB, gần A, cách A một đoạn x (m)
\(\begin{array}{l}{E_{1M}} = {E_{2M}} \Leftrightarrow k\dfrac{{\left| {{q_1}} \right|}}{{\varepsilon M{A^2}}} = k\dfrac{{\left| {{q_2}} \right|}}{{\varepsilon M{B^2}}}\\ \Leftrightarrow \dfrac{{{{16.10}^{ - 9}}}}{{{x^2}}} = \dfrac{{{{36.10}^{ - 9}}}}{{{{\left( {x + 0,1} \right)}^2}}} \Leftrightarrow x = 0,2m = 20cm\end{array}\)
Một điện tích điểm \(Q = + {4.10^{ - 8}}C\) đặt tại một điểm \(O\) trong không khí. Cường độ điện trường tại điểm \(M\), cách \(O\) một khoảng \(2 cm\) do \(Q\) gây ra là
Cường độ điện trường tại M do Q gây ra là \(E = \dfrac{{k\left| Q \right|}}{{\varepsilon {r^2}}} = {9.10^5}(V/m)\;\;\;\)
Một hạt bụi tích điện có khối lượng m = 10-8g nằm cân bằng trong điện trường đều có hướng thẳng đứng xuống dưới và có cường độ E = 1000 V/m, lấy g =10 m/s2. Điện tích của hạt bụi là
Ta có:
\(F = P \Leftrightarrow \left| q \right|E = mg \Leftrightarrow \left| q \right| = \dfrac{{mg}}{E} = \dfrac{{{{10}^{ - 8}}{{.10}^{ - 3}}.10}}{{1000}} = {10^{ - 13}}C\)
Hạt bụi nằm cân bằng nên Fđ hướng lên => q < 0
\( \Rightarrow q = - {10^{ - 13}}C\)
Cho hình vuông ABCD, tại A và C đặt các điện tích dương \(q_1 = q_3 = q.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
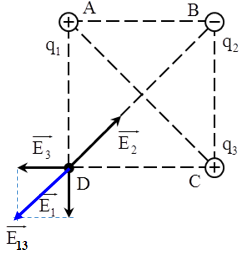
+ Cường độ điện trường tổng hợp tại D:\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} \) lần lượt là vecto cường độ điện trường do các điện tích \({q_1};{q_2};{q_3}\)gây ra tại D.
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AD = CD \end{matrix}\right. \Rightarrow E_1 = E_3 \Rightarrow E_{13} = \sqrt {2}E_1 = \sqrt {2}.\dfrac{k\left | q \right |}{a^2}\)
+ Ta có: \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Để cường độ điện trường tại O triệt tiêu thì
\(\overrightarrow {{E_D}} = 0 \Leftrightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_{13}} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_2}} \) hướng lại gần \({q_2} \Rightarrow {q_2} < 0\)
Từ (2) ta có:
\({E_2} = {E_{13}} \Leftrightarrow \dfrac{{k\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \sqrt 2 .\dfrac{{k\left| q \right|}}{{{a^2}}} \Rightarrow \left| {{q_2}} \right| = 2\sqrt 2 .\left| q \right| = 2\sqrt 2 \left| q \right|\)
\(\Rightarrow q_2 = - 2\sqrt{2}q.\)
Lần lượt đặt hai điện tích thử q1, q2 (q1 = 2q2) vào hai điểm A và B trong điện trường. Độ lớn lực điện tác dụng lên q1, q2 lần lượt là F1 và F2, với F1 = 5F2. Độ lớn cường độ điện trường tại A và B là E1 và E2 thỏa mãn
Ta có: \(F = E.q\)
Suy ra: \(\dfrac{F_2}{F_1}=\dfrac{E_2q_2}{E_1q_1}\)
Lại có \(F_1=5F_2\) và \(q_1=2q_2\)
Ta suy ra: \(\dfrac{F_2}{5F_2}=\dfrac{E_2q_2}{E_1.2q_2}\)
=> \({E_2} = 0,4{E_1}\)
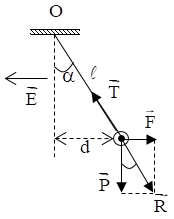
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tính điện tích của quả cầu.
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
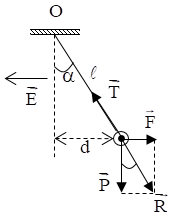
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\tan \alpha = \dfrac{d}{{\sqrt {{l^2} - {d^2}} }} = \dfrac{F}{P} \Leftrightarrow \dfrac{1}{{\sqrt {{2^2} - {1^2}} }} = \dfrac{{\left| q \right|E}}{{mg}} \Rightarrow \left| q \right| = \dfrac{{mg}}{{E\sqrt 3 }}\)
\( \Rightarrow \left| q \right| = \dfrac{{4,{{5.10}^{ - 3}}.10}}{{2000\sqrt 3 }} = 1,{3.10^{ - 5}}C\)
Do \(\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow E \Rightarrow q < 0 \Rightarrow q = - 1,{3.10^{ - 5}}C\)
Đặt hai điện tích điểm \({q_1} = - {q_2}\) lần lượt tại A và B thì cường độ điện trường tổng hợp gây ra tại M nằm trên trung trực của AB có phương
Điểm M nằm trên đường trung trực của AB, ta có: \(AM = BM\)
Cường độ điện trường do hai điện tích gây ra tại M là:
\(\left\{ \begin{array}{l}{E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{\varepsilon .A{M^2}}}\\{E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{\varepsilon .B{M^2}}}\end{array} \right. \Rightarrow {E_1} = {E_2}\)
Ta có hình vẽ:
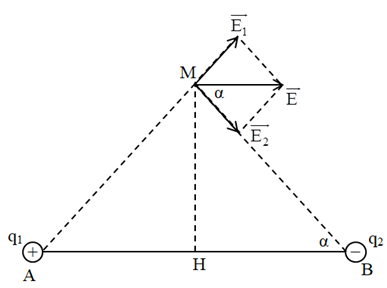
Từ hình vẽ ta thấy vecto cường độ điện trường tổng hợp tại M song song với AB
Hai điện tích \({q_1} = {q_2} = 5nC\), đặt tại hai điểm \(A\)và B cách nhau 8cm trong không khí. Cường độ điện trường do hai điện tích gây ra tại điểm N cách A một đoạn 2 cm và cách B một đoạn 10cm có độ lớn bằng bao nhiêu?
Ta có NA = 2cm, NB = 10cm và AB = 8cm nên N nằm trên đường thẳng AB và nằm ngoài AB.
Cường độ điện trường tổng hợp tại N: \({\vec E_N} = \overrightarrow {{E_1}} {\rm{\;}} + \overrightarrow {{E_2}} \)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{N^2}}} = {{9.10}^9}.\dfrac{{{{5.10}^{ - 9}}}}{{0,{{02}^2}}} = 1,{{125.10}^5}(V/m)}\\{{E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{N^2}}} = {{9.10}^9}.\dfrac{{{{5.10}^{ - 9}}}}{{0,{1^2}}} = 4500(V/m)}\end{array}} \right.\)
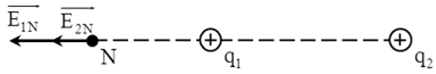
Từ hình vẽ ta có: \(\overrightarrow {{E_1}} {\rm{\;}} \uparrow {\rm{\;}} \uparrow \overrightarrow {{E_2}} {\rm{\;}} \Rightarrow {E_N} = {E_1} + {E_2} = 11,{7.10^4}(V/m)\)
Tại điểm B đặt thêm \({q_2} = - {16.10^{ - 6}}C\). Biết AB = 40 cm; BC = 30 cm. Xác định cường độ điện trường tổng hợp do q1 và q2 gây ra tại điểm C.
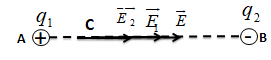
Ta có:
\({E_2} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon .B{C^2}}} = {9.10^9}.\frac{{\left| {{{16.10}^{ - 6}}} \right|}}{{0,{3^2}}} = {16.10^5}V/m\)
Cường độ điện trường tổng hợp do q1 và q2 gây ra tại C là:
\(\overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2}\)
Có phương chiều được biểu diễn như hình vẽ.
Có độ lớn: \(E = {E_1} + {E_2} = {36.10^5} + {16.10^5} = {52.10^5}V/m\)
Xác định độ lớn cường độ điện trường do q1 gây ra tại C cách A 10cm.
Độ lớn cường độ điện trường do q1 gây ra tại C là:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{C^2}}} = {9.10^9}.\dfrac{{\left| {{{4.10}^{ - 6}}} \right|}}{{0,{1^2}}} = {36.10^5}V/m\)
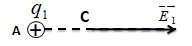
Ba điểm \({\rm{O}},{\rm{A}},{\rm{B}}\) theo thứ tự thẳng hàng ở trong không khí. Tại O đặt điện tích điểm \({\rm{Q}}\), cường độ điện trường do \({\rm{Q}}\) tạo ra tại \({\rm{A}}\) gấp 9 lần tại \({\rm{B}}\). Tỷ số khoảng cách \(\dfrac{{{\rm{OB}}}}{{{\rm{OA}}}}\) là
Từ công thức:\(E = \dfrac{{k\left| Q \right|}}{{\varepsilon .{r^2}}} \Rightarrow \left\{ \begin{array}{l}{E_A} = \dfrac{{k\left| Q \right|}}{{\varepsilon .O{A^2}}}\\{E_B} = \dfrac{{k\left| Q \right|}}{{\varepsilon .O{B^2}}}\end{array} \right.\)
\( \Rightarrow \dfrac{{{E_A}}}{{{E_B}}} = \dfrac{{O{B^2}}}{{O{A^2}}} = 9 \Rightarrow \dfrac{{OB}}{{OA}} = 3\)
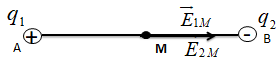
Hai điện tích điểm q1 = 4.10-8C và q2 = -4.10-8C nằm cố định tại hai điểm A và B cách nhau 20 cm trong không khí. Xác định vec tơ cường độ điện trường E tại điểm M là trung điểm của AB.
Điểm M là trung điểm của AB.
Ta biểu diễn vecto cường độ điện trường \(\overrightarrow {{E_{1M}}} ;\overrightarrow {{E_{2M}}} \) như hình vẽ.
Ta có:
Vecto cường độ điện trường tổng hợp: \(\overrightarrow E = \overrightarrow {{E_{1M}}} + \overrightarrow {{E_{2M}}} \)
\(\overrightarrow {{E_{1M}}} \uparrow \uparrow \overrightarrow {{E_{2M}}} \Rightarrow E = {E_{1M}} + {E_{2M}}\)
Lại có:
\({E_{1M}} = {E_{2M}} = k\frac{{\left| q \right|}}{{\varepsilon {r^2}}} = {9.10^9}.\frac{{{{4.10}^{ - 8}}}}{{0,{1^2}}} = 36000V/m\)
Suy ra: \(E = {E_{1M}} + {E_{2M}} = 2.36000 = 72000V/m\)
Hai điện tích điểm q1 = 4.10-8C và q2 = -4.10-8C nằm cố định tại hai điểm A và B cách nhau 20 cm trong không khí. Xác định vec tơ cường độ điện trường E tại điểm N cách A 10cm, cách B 30 cm.
N cách A 10cm, cách B 30cm
Ta biểu diễn vecto cường độ điện trường \(\overrightarrow {{E_{1M}}} ;\overrightarrow {{E_{2M}}} \) như hình vẽ.
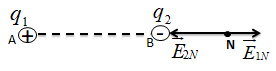
Ta có:
\({E_{1M}} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon r_{1M}^2}} = {9.10^9}.\frac{{\left| {{{4.10}^{ - 8}}} \right|}}{{0,{1^2}}} = 36000V/m\)
\({E_{2M}} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon r_{2M}^2}} = {9.10^9}.\frac{{\left| { - {{4.10}^{ - 8}}} \right|}}{{0,{3^2}}} = 4000V/m\)
Vecto cường độ điện trường tổng hợp: \(\overrightarrow E = \overrightarrow {{E_{1M}}} + \overrightarrow {{E_{2M}}} \)
\(\overrightarrow {{E_{1M}}} \uparrow \downarrow \overrightarrow {{E_{2M}}} \Rightarrow E = \left| {{E_{1M}} - {E_{2M}}} \right| = 32000V/m\)
Quả cầu nhỏ mang điện tích \({10^{ - 9}}C\) đặt trong không khí. Cường độ điện trường tại 1 điểm cách quả cầu \(3cm\) là
Ta có, cường độ điện trường \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}} = {9.10^9}.\dfrac{{{{10}^{ - 9}}}}{{1.{{\left( {0,03} \right)}^2}}} = 10000V/m = {10^4}V/m\)
Một điện tích điểm \(Q\) đặt trong một môi trường đồng tính, vô hạn có hằng số điện môi bằng \(2,5\). Tại điểm M cách \(Q\) một đoạn \(0,4m\) véctơ cường độ điện trường có độ lớn bằng \({9.10^4}V/m\) và hướng về phía điện tích \(Q\). Khẳng định nào sau đây đúng khi nói về dấu và độ lớn của điện tích \(Q\) ?
Ta có:
+ Véctơ cường độ điện trường hướng về phía điện tích \(Q\) nên \(Q < 0\) (1)
+ Mặt khác, \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)
Ta suy ra: \(\left| Q \right| = \dfrac{{E.\varepsilon .{r^2}}}{k} = \dfrac{{{{9.10}^4}.2,5.{{\left( {0,4} \right)}^2}}}{{{{9.10}^9}}} = {4.10^{ - 6}}C = 4\mu C\)
Kết hợp với (1) ta suy ra: \(Q = - 4\mu C\)
Một điện tích điểm \(q = - 2,{5.10^{ - 7}}C\) đặt tại điểm M trong điện trường, chịu tác dụng của lực điện trường có độ lớn \(6,{2.10^{ - 2}}N\) . Cường độ điện trường tại M là:
Ta có, cường độ điện trường E:
\(E = \dfrac{F}{{\left| q \right|}} = \dfrac{{6,{{2.10}^{ - 2}}}}{{\left| { - 2,{{5.10}^{ - 7}}} \right|}} = 248000V/m = 2,{48.10^5}V/m\)
Một điện tích Q trong nước \(\left( {\varepsilon = 81} \right)\) gây ra tại điểm M cách điện tích một khoảng \(r = 26cm\) một điện trường \(E = 1,{5.10^4}V/m\). Hỏi tại điểm N cách điện tích \(Q\) một khoảng \(r = 17cm\) có cường độ điện trường bằng bao nhiêu ?
Ta có:
+ Cường độ điện trường tại M: \({E_M} = k\dfrac{{\left| Q \right|}}{{\varepsilon r_M^2}}\)
+ Cường độ điện trường tại N: \({E_N} = k\dfrac{{\left| Q \right|}}{{\varepsilon r_N^2}}\)
Ta suy ra:
\(\begin{array}{l}\dfrac{{{E_M}}}{{{E_N}}} = \dfrac{{r_N^2}}{{r_M^2}} = \dfrac{{0,{{17}^2}}}{{0,{{26}^2}}}\\ \Rightarrow {E_N} \approx 3,{5.10^4}V/m\end{array}\)
Một điện tích điểm q đặt trong một môi trường đồng tính có hằng số điện môi bằng 2. Tại điểm M cách q một đoạn 0,5m véctơ cường độ điện trường có độ lớn là \({9.10^4}V/m\) và hướng về phía điện tích \(q\). Giá trị của điện tích \(q\) là
Ta có: \(E = k\dfrac{{\left| q \right|}}{{\varepsilon {r^2}}} \Leftrightarrow {9.10^4} = {9.10^9}\dfrac{{\left| q \right|}}{{2.0,{5^2}}}\)
\( \Rightarrow \left| q \right| = {5.10^{ - 6}}m\)
Lại có, véctơ cường độ điện trường hướng về phía điện tích \(q\)
\( \Rightarrow q < 0 \Rightarrow q = - 5\mu m\)
Cường độ điện trường do điện tích \( + Q\) gây ra tại điểm A cách nó một khoảng \(r\) có độ lớn là \(E\). Nếu khoảng cách từ điện tích nguồn đến điểm đang xét tăng 2 lần thì cường độ điện trường:
Ta có:
+ Ban đầu: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)
+ Khi tăng khoảng cách từ điện tích nguồn đến điểm đang xét tăng lên 2 lần tức là \(r' = 2r\)
Khi đó: \(E' = k\dfrac{{\left| Q \right|}}{{\varepsilon r{'^2}}} = k\dfrac{{\left| Q \right|}}{{\varepsilon 4{r^2}}} = \dfrac{E}{4}\)
=> Cường độ điện trường giảm 4 lần.