Câu hỏi:
2 năm trước
Hai điện tích \({q_1} = {q_2} = 5nC\), đặt tại hai điểm \(A\)và B cách nhau 8cm trong không khí. Cường độ điện trường do hai điện tích gây ra tại điểm N cách A một đoạn 2 cm và cách B một đoạn 10cm có độ lớn bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có NA = 2cm, NB = 10cm và AB = 8cm nên N nằm trên đường thẳng AB và nằm ngoài AB.
Cường độ điện trường tổng hợp tại N: \({\vec E_N} = \overrightarrow {{E_1}} {\rm{\;}} + \overrightarrow {{E_2}} \)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{N^2}}} = {{9.10}^9}.\dfrac{{{{5.10}^{ - 9}}}}{{0,{{02}^2}}} = 1,{{125.10}^5}(V/m)}\\{{E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{N^2}}} = {{9.10}^9}.\dfrac{{{{5.10}^{ - 9}}}}{{0,{1^2}}} = 4500(V/m)}\end{array}} \right.\)
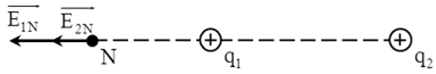
Từ hình vẽ ta có: \(\overrightarrow {{E_1}} {\rm{\;}} \uparrow {\rm{\;}} \uparrow \overrightarrow {{E_2}} {\rm{\;}} \Rightarrow {E_N} = {E_1} + {E_2} = 11,{7.10^4}(V/m)\)
Hướng dẫn giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường:
\(\vec E = \overrightarrow {{E_1}} {\rm{\;}} + \overrightarrow {{E_2}} {\rm{\;}} + ... + \overrightarrow {{E_n}} \)
