Thả một electron không vận tốc đầu ban đầu trong một điện trường bất kì, electron sẽ:
Cường độ điện trường hướng từ nơi có điện thế cao đến nơi có điện thế thấp.
Electron mang điện tích âm nên chịu tác dụng của lực điện trường và lực điện ngược chiều với cường độ điện trường.
=> Electron sẽ chuyển động từ một điểm có điện thế thấp lên điểm có điện thế cao.
Nối hai cực của nguồn điện không đổi có hiệu điện thế \(110V\) lên hai bản của tụ điện phẳng có khoảng cách giữa hai bản tụ bằng \(5cm\). Trong vùng không gian giữa hai bản tụ, 1 proton có điện tích \(1,{6.10^{ - 19}}C\) và khối lượng \(1,{67.10^{ - 27}}kg\) chuyển động từ điểm M cách bản âm của tụ điện \(4cm\) đến điểm N cách bản âm của tụ \(1cm\). Biết tốc độ của proton tại M bằng \({2.10^5}m/s\). Tốc độ của proton tại N bằng:
Ta có:
+ Cường độ điện trường giữa hai bản tụ điện là:
\(E = \dfrac{U}{d} = \dfrac{{110}}{{0,05}} = 2200V/m\).
+ Lực điện trường tác dụng lên điện tích là \(F = qE = 1,{6.10^{ - 19}}.2200 = 3,{52.10^{ - 16}}N\).
+ Định luật II Niuton có \(F = ma\)
=> điện tích di chuyển trong điện trường với gia tốc \(a = \dfrac{F}{m} = \dfrac{{3,{{52.10}^{ - 16}}}}{{1,{{67.10}^{ - 27}}}} = 2,{11.10^{11}}m/{s^2}\)
\( \to v_N^2 - v_M^2 = 2as \\\Rightarrow {v_N} = \sqrt {2.2,{{11.10}^{11}}.\left( {0,03} \right) + {{\left( {{{2.10}^5}} \right)}^2}} \\= 2,{3.10^5}m/s\).
Hiệu điện thế giữa hai bản tụ điện phẳng bằng \(U = 220{\rm{ }}V\). Một hạt bụi nằm cân bằng giữa hai bản tụ điện và cách bản dưới của tụ điện \({d_1} = 2cm\). Hỏi trong bao nhiêu lâu hạt bụi sẽ rơi xuống mặt bản tụ, nếu hiệu điện thế giữa hai bản giảm đi một lượng \(\Delta U = 50{\rm{ }}V\).
Hạt bụi nằm cân bằng chịu tác dụng của trọng lực P và lực điện F: \(P = F\)
- Trước khi giảm U: \(P = mg.q.E = q.\dfrac{U}{d} \to m = \dfrac{{qU}}{{dg}}\)
- Sau khi giảm U: \({F_1} = \dfrac{{q\left( {U - \Delta U} \right)}}{d}\)
Hiệu lực \(F - {F_1}\) gây ra gia tốc cho hạt bụi:
\(F - {F_1} = \dfrac{{q.\Delta U}}{d} = m.a\)
\( \Rightarrow a = \dfrac{{\Delta U.g}}{U}\)
Ta có: \({d_1} = \dfrac{{a{t^2}}}{2} \to t = \sqrt {\dfrac{{2{d_1}}}{a}} = \sqrt {\dfrac{{2{d_1}U}}{{\Delta U.g}}} = \sqrt {\dfrac{{2.0,02.220}}{{50.10}}} = 0,133s\)
Một quả cầu tích điện có khối lượng \(1mg\) nằm cân bằng giữa hai bản tụ điện phẳng, đứng cách nhau \(d = 2cm\). Khi hai bản tụ được nối với hiệu điện thế \(U = 220{\rm{ }}V\) thì dây treo quả cầu lệch khỏi phương thẳng đứng một góc \(\alpha = {10^0}\). Điện tích của quả cầu bằng:
+ Các lực tác dụng lên quả cầu \(\overrightarrow P ,\overrightarrow F ,\overrightarrow T \):
+ Quả cầu cân bằng => \(\overrightarrow P + \overrightarrow F + \overrightarrow T = \overrightarrow 0 \)
+ Ta có: \(F = P\tan \alpha = {q_0}.E = {q_0}.\dfrac{U}{d}\)
\( \Rightarrow {q_0} = \dfrac{{mgd\tan \alpha }}{U} = \dfrac{{\left( {{{1.10}^{ - 3}}{{.10}^{ - 3}}} \right).10.0,02.\tan 10^\circ }}{{220}} = 1,{6.10^{ - 10}}C\)
Nếu hạt bụi mất đi một nửa số electron có thừa thì hạt bụi sẽ chuyển động như thế nào?
+ Biểu thức định luật II Niu-tơn: \(\overrightarrow F + \overrightarrow P = m\overrightarrow a \) (1)
Chọn chiều dương là chiều chuyển động của vật, ta có (1) tương đương với \(P - F = ma\)
+ Khi mất bớt đi một nửa điện tích thì F giảm đi một nửa nên \(P > F\)
\( \Rightarrow \) hạt sẽ chuyển động đi xuống nhanh nhần đều với gia tốc \(a = \dfrac{{P - F}}{m}\)
\(a = \dfrac{{mg - \dfrac{q}{2}E}}{m} = \dfrac{{mg - \dfrac{{mg}}{2}}}{m} = \dfrac{g}{2} = 5m/{s^2}\)
Vậy, nếu hạt bụi mất đi một nửa số electron có thừa thì hạt bụi sẽ chuyển động nhanh dần đều đi xuống với gia tốc \(a = 5m/{s^2}\)
Tính lượng electron thừa trong hạt bụi. Biết điện tích của electron \(e = - 1,{6.10^{ - 19}}C\)
+ Ta có, các lực tác dụng lên hạt bụi gồm lực điện và trọng lực
Hạt bụi nằm lơ lửng (tức là cân bằng) ta có các lực tác dụng lên hạt bụi: \(\overrightarrow {{F_d}} + \overrightarrow P = \overrightarrow 0 \)
Hay \({F_d} = P \Leftrightarrow qE = mg\)
\( \Rightarrow q = \dfrac{{mgd}}{U}\)
Ta suy ra, số hạt electron thừa trong hạt bụi là: \(n = \dfrac{q}{{\left| e \right|}} = \dfrac{{mgd}}{{U\left| e \right|}} = \dfrac{{{{10}^{ - 7}}{{.10}^{ - 3}}.10.\left( {0,{{5.10}^{ - 2}}} \right)}}{{31,25.1,{{6.10}^{ - 19}}}} = {10^6}\)
Tính lượng electron thừa trong hạt bụi. Biết điện tích của electron \(e = - 1,{6.10^{ - 19}}C\)
+ Ta có, các lực tác dụng lên hạt bụi gồm lực điện và trọng lực
Hạt bụi nằm lơ lửng (tức là cân bằng) ta có các lực tác dụng lên hạt bụi: \(\overrightarrow {{F_d}} + \overrightarrow P = \overrightarrow 0 \)
Hay \({F_d} = P \Leftrightarrow qE = mg\)
\( \Rightarrow q = \dfrac{{mgd}}{U}\)
Ta suy ra, số hạt electron thừa trong hạt bụi là: \(n = \dfrac{q}{{\left| e \right|}} = \dfrac{{mgd}}{{U\left| e \right|}} = \dfrac{{{{10}^{ - 7}}{{.10}^{ - 3}}.10.\left( {0,{{5.10}^{ - 2}}} \right)}}{{31,25.1,{{6.10}^{ - 19}}}} = {10^6}\)
Gia tốc của electron trong điện trường đều có giá trị là:
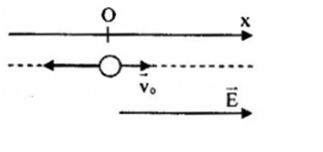
Chọn trục Ox, có gốc O là vị trí mà electon bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.
Khi bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)
+ Theo định luật II - Niutơn, ta có: \(\overrightarrow F = m\overrightarrow a \) (1)
+ Vì \(q = e < 0 \to \overrightarrow F \uparrow \downarrow \overrightarrow E \), mà \(\overrightarrow {{v_0}} \) cùng hướng với \(\overrightarrow E \) nên \(\overrightarrow F \) ngược chiều dương.
Chiếu (1) lên Ox, ta được:
\(\begin{array}{l} - F = ma \leftrightarrow - \left| q \right|E = ma\\ \to a = \frac{{ - \left| { - 1,{{6.10}^{ - 19}}} \right|910}}{{9,{{1.10}^{ - 31}}}} = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\end{array}\)
=> electron chuyển động chậm dần với gia tốc: \(a = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\)
Độ lệch \(h\) của electron khi bắt đầu ra khỏi điện trường. Biết hiệu điện thế \(U = 50V\) và khoảng cách giữa hai bản \(d = 10cm\).

Ta có:
+ Gia tốc của electron khi bay vào trong điện trường của hai bản tụ:
\(a = \dfrac{F}{m}\)
Lại có: \(F = \left| q \right|E = \left| q \right|\dfrac{U}{d}\)
Suy ra: \(a = \dfrac{{\left| q \right|U}}{{md}} = \dfrac{{1,{{6.10}^{ - 19}}.50}}{{9,{{1.10}^{ - 31}}.0,1}} = 8,{79.10^{13}}m/{s^2}\)
+ Phương trình chuyển động theo trục Oy: \(y = \dfrac{1}{2}a{t^2} = 4,{395.10^{13}}{t^2}\)
+ Khi ra khỏi bản tụ thì: \(t = 2,{5.10^{ - 8}}s\) (tính ở câu trên)
Nên \(h = y = 4,{395.10^{13}}{\left( {2,{{5.10}^{ - 8}}} \right)^2} = 0,0275m = 2,75cm\)
Thời gian đi hết chiều dài \(5cm\) của bản.
Ta có, electron tham gia chuyển động giống như chuyển động của một vật bị ném ngang với vận tốc đầu \({v_0} = {2.10^6}m/s\) (đã tính được ở câu trên)
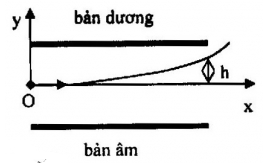
+ Theo phương ngang (phương Ox), electron không chịu tác dụng của lực nào nên nó chuyển động thẳng đều với phương trình chuyển động: \(x = {v_0}t = {2.10^6}t\)
+ Khi electron đi hết chiều dài \(5cm\) của bản thì: \(x = L\)
\(\begin{array}{l} \Leftrightarrow {2.10^6}t = 0,05\\ \Rightarrow t = 2,{5.10^{ - 8}}s\end{array}\)
Vận tốc \({v_0}\) của electron lúc bắt đầu vào điện trường.
Ta có,
\(\begin{array}{l}{{\rm{W}}_{{d_0}}} = \dfrac{1}{2}mv_0^2\\ \Rightarrow {v_0} = \sqrt {\dfrac{{2{W_{{d_0}}}}}{m}} = \sqrt {\dfrac{{2.11,375.1,{{9.10}^{ - 19}}}}{{9,{{1.10}^{ - 31}}}}} = 2,{18.10^6}m/s\end{array}\)
Vận tốc \({v_0}\) của electron lúc bắt đầu vào điện trường.
Ta có,
\(\begin{array}{l}{{\rm{W}}_{{d_0}}} = \dfrac{1}{2}mv_0^2\\ \Rightarrow {v_0} = \sqrt {\dfrac{{2{W_{{d_0}}}}}{m}} = \sqrt {\dfrac{{2.11,375.1,{{9.10}^{ - 19}}}}{{9,{{1.10}^{ - 31}}}}} = 2,{18.10^6}m/s\end{array}\)
Một electron có điện tích e, khối lượng m, vận tốc v đi vào một điện trường đều có cường độ điện trường E như hình vẽ. Quãng đường x mà electron đi được ngay trước khi dừng lại là

Nhận xét: lực điện tác dụng lên electron ngược chiều điện trường
→ electron chuyển động chậm dần đều
Lực điện tác dụng lên electron là:
\({F_d} = - E.e = ma \Rightarrow a = \dfrac{{ - E.e}}{m}\)
Ngay khi dừng lại, quãng đường electron dịch chuyển được là
\(s = \dfrac{{{v^2} - {v_0}^2}}{{2a}} = \dfrac{{{0^2} - {v^2}}}{{2.\dfrac{{ - E.e}}{m}}} = \dfrac{{m{v^2}}}{{2E.e}}\)
Quãng đường mà electron đi được cho đến khi dừng lại là:
Ta có:
+ Gia tốc chuyển động của electron khi chuyển động trong điện trường: \(a = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\) (tính ở câu trên)
+ Lại có: \({v^2} - v_0^2 = 2a{\rm{s}}\)
+ Electron dừng lại: v = 0
Ta suy ra: \(s = \frac{{0 - v_0^2}}{{2{\rm{a}}}} = \frac{{0 - {{\left( {3,{{2.10}^6}} \right)}^2}}}{{2.\left( { - 1,{{6.10}^{14}}} \right)}} = 0,032m = 3,2cm\)
Thời gian mà electron chuyển động cho đến khi dừng lại là:
Ta có:
Gia tốc chuyển động của electron khi chuyển động trong điện trường: \(a = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\) (tính ở câu trên)
+ Phương trình vận tốc: \(v = {v_0} + at\)
+ Electron dừng lại: \(v = 0 = {v_0} + at \to t = \frac{{ - {v_0}}}{a} = \frac{{3,{{2.10}^6}}}{{1,{{6.10}^{14}}}} = {2.10^{ - 8}}s\)
Gia tốc của electron trong điện trường đều có giá trị là:

Chọn trục Ox, có gốc O là vị trí mà electon bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.
Khi bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)
+ Theo định luật II - Niutơn, ta có: \(\overrightarrow F = m\overrightarrow a \) (1)
+ Vì \(q = e < 0 \to \overrightarrow F \uparrow \downarrow \overrightarrow E \), mà \(\overrightarrow {{v_0}} \) cùng hướng với \(\overrightarrow E \) nên \(\overrightarrow F \) ngược chiều dương.
Chiếu (1) lên Ox, ta được:
\(\begin{array}{l} - F = ma \leftrightarrow - \left| q \right|E = ma\\ \to a = \frac{{ - \left| { - 1,{{6.10}^{ - 19}}} \right|910}}{{9,{{1.10}^{ - 31}}}} = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\end{array}\)
=> electron chuyển động chậm dần với gia tốc: \(a = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\)
Gia tốc của electron trong điện trường đều có giá trị là:

Chọn trục Ox, có gốc O là vị trí mà electon bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.
Khi bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)
+ Theo định luật II - Niutơn, ta có: \(\overrightarrow F = m\overrightarrow a \) (1)
+ Vì \(q = e < 0 \to \overrightarrow F \uparrow \downarrow \overrightarrow E \), mà \(\overrightarrow {{v_0}} \) cùng hướng với \(\overrightarrow E \) nên \(\overrightarrow F \) ngược chiều dương.
Chiếu (1) lên Ox, ta được:
\(\begin{array}{l} - F = ma \leftrightarrow - \left| q \right|E = ma\\ \to a = \frac{{ - \left| { - 1,{{6.10}^{ - 19}}} \right|910}}{{9,{{1.10}^{ - 31}}}} = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\end{array}\)
=> electron chuyển động chậm dần với gia tốc: \(a = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\)
Electron quay quanh hạt nhân nguyên tử hidro theo quỹ đạo tròn, bán kính r = 5.10-11 m. Tính vận tốc dài của electron ntrên quỹ đạo. Biết khối lượng của electron là m = 9,1.10-31 kg.
Chuyển động tròn đều, lực điện bằng lực hướng tâm, ta có:
\(\begin{array}{l}{F_d} = {F_{ht}} \Leftrightarrow k\dfrac{{{e^2}}}{{{r^2}}} = \dfrac{{m{v^2}}}{r}\\ \Leftrightarrow v = e\sqrt {\dfrac{k}{{m{\rm{r}}}}} = 1,{6.10^{ - 19}}.\sqrt {\dfrac{{{{9.10}^9}}}{{9,{{1.10}^{ - 31}}{{.5.10}^{ - 11}}}}} = 22,{5.10^5}m/s\end{array}\)
Thả một ion dương cho chuyển động không vận tốc đầu từ một điểm bất kì trong một điện trường do hai điện tích điểm dương gây ra. Ion đó sẽ chuyển động
Cường độ điện trường hướng từ nơi có điện thế cao đến nơi có điện thế thấp. Ion dương nên lực điện cùng chiều với cường độ điện trường.
=> Ion dương sẽ chuyển động từ điểm có điện thế cao đến điểm có điện thế thấp.
Nối hai cực của nguồn điện không đổi có hiệu điện thế $50V$ lên hai bản của tụ điện phẳng có khoảng cách giữa hai bản tụ bằng $5cm$. Trong vùng không gian giữa hai bản tụ, $1$ proton có điện tích \(1,{6.10^{ - 19}}C\) và khối lượng \(1,{67.10^{ - 27}}kg\) chuyển động từ điểm M cách bản âm của tụ điện $4cm$ đến điểm N cách bản âm của tụ $1cm$. Biết tốc độ của proton tại M bằng \({10^5}m/s\). Tốc độ của proton tại N bằng:
Ta có:
+ Cường độ điện trường giữa hai bản tụ điện là:
\(E = \dfrac{U}{d} = \dfrac{{50}}{{0,05}} = 1000V/m\).
+ Lực điện trường tác dụng lên điện tích là \(F = qE = 1,{6.10^{ - 19}}.1000 = 1,{6.10^{ - 16}}N\).
+ Định luật II Niuton có \(F = ma\)
=> điện tích di chuyển trong điện trường với gia tốc \(a = \dfrac{F}{m} = \dfrac{{1,{{6.10}^{ - 16}}}}{{1,{{67.10}^{ - 27}}}} = 9,{58.10^{10}}m/{s^2}\)
\( \to v_N^2 - v_M^2 = 2as \Rightarrow {v_N} = \sqrt {2.9,{{58.10}^{10}}.0,03 + {{\left( {{{10}^5}} \right)}^2}} = 1,{25.10^5}m/s\).

