Bài tập chuyển động của điện tích trong điện trường

Hạt bụi nằm cân bằng chịu tác dụng của trọng lực P và lực điện F: \(P = F\)

- Trước khi giảm U: \(P = mg.q.E = q.\frac{U}{d} \to m = \frac{{qU}}{{dg}}\)

- Sau khi giảm U: \({F_1} = \frac{{q\left( {U - \Delta U} \right)}}{d}\)

Hiệu lực \(F - {F_1}\)  gây ra gia tốc cho hạt bụi:

\(F - {F_1} = \frac{{q.\Delta U}}{d} = m.a\) 

 \( \Rightarrow a = \frac{{\Delta U.g}}{U}\)

Ta có: \({d_1} = \frac{{a{t^2}}}{2} \to t = \sqrt {\frac{{2{d_1}}}{a}}  = \sqrt {\frac{{2{d_1}U}}{{\Delta U.g}}}  = 0,09s\) 

+ Các lực tác dụng lên quả cầu \(\overrightarrow P ,\overrightarrow F ,\overrightarrow T \):

+ Quả cầu cân bằng => \(\overrightarrow P  + \overrightarrow F  + \overrightarrow T  = \overrightarrow 0 \)

+ Ta có: \(F = P\tan \alpha  = {q_0}.E = {q_0}.\frac{U}{d}\)

\( \Rightarrow {q_0} = \frac{{mgd\tan \alpha }}{U} = \frac{{0,{{1.10}^{ - 3}}.0,01.10.\tan 10^\circ }}{{1000}} = 1,{76.10^{ - 9}}C\)

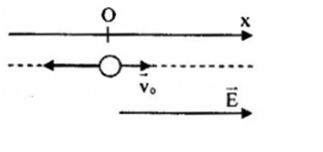
Chọn trục Ox, có gốc O là vị trí mà electon bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.

Khi  bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)

+ Theo định luật II - Niutơn, ta có: \(\overrightarrow F  = m\overrightarrow a \)  (1)

+ Vì \(q = e < 0 \to \overrightarrow F  \uparrow  \downarrow \overrightarrow E \), mà \(\overrightarrow {{v_0}} \) cùng hướng với \(\overrightarrow E \) nên \(\overrightarrow F \) ngược chiều dương.

Chiếu (1) lên Ox, ta được:

\(\begin{array}{l} - F = ma \leftrightarrow  - \left| q \right|E = ma\\ \to a = \frac{{ - \left| { - 1,{{6.10}^{ - 19}}} \right|910}}{{9,{{1.10}^{ - 31}}}} =  - 1,{6.10^{14}}\left( {m/{s^2}} \right)\end{array}\)

=> electron chuyển động chậm dần với gia tốc: \(a =  - 1,{6.10^{14}}\left( {m/{s^2}} \right)\)   

Ta có:

Gia tốc chuyển động của electron khi chuyển động trong điện trường: \(a =  - 1,{6.10^{14}}\left( {m/{s^2}} \right)\) (tính ở câu trên)

+ Phương trình vận tốc: \(v = {v_0} + at\)

+ Electron dừng lại: \(v = 0 = {v_0} + at \to t = \frac{{ - {v_0}}}{a} = \frac{{3,{{2.10}^6}}}{{1,{{6.10}^{14}}}} = {2.10^{ - 8}}s\)

Ta có:

+ Gia tốc chuyển động của electron khi chuyển động trong điện trường: \(a =  - 1,{6.10^{14}}\left( {m/{s^2}} \right)\) (tính ở câu trên)

+ Lại có: \({v^2} - v_0^2 = 2a{\rm{s}}\)

+ Electron dừng lại: v = 0

Ta suy ra: \(s = \frac{{0 - v_0^2}}{{2{\rm{a}}}} = \frac{{0 - {{\left( {3,{{2.10}^6}} \right)}^2}}}{{2.\left( { - 1,{{6.10}^{14}}} \right)}} = 0,032m = 3,2cm\)

Chọn chiều dương là chiều của véctơ \(\overrightarrow E \)

Giả sử \({q_1} > 0;{q_2} < 0\), khi đó hạt mang điện tích \({q_1}\) sẽ chuyển động theo chiều điện trường, hạt mang điện tích $q_2$ sẽ chuyển động ngược chiều điện trường.

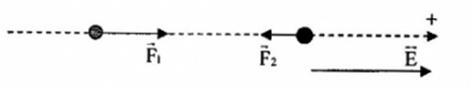
+ Biểu thức định luật II - Niutơn cho mỗi hạt: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  = {m_1}\overrightarrow {{a_1}} \\\overrightarrow {{F_2}}  = {m_2}\overrightarrow {{a_2}} \end{array} \right.\)

+ Chiếu lên chiều dương đã chọn, ta có: \(\left\{ \begin{array}{l}{F_1} = {m_1}{a_1}\\ - {F_2} = {m_2}{a_2}\end{array} \right.\)

.\( \to \left\{ \begin{array}{l}{a_1} = \dfrac{{{F_1}}}{{{m_1}}} = \dfrac{{\left| q \right|E}}{{{m_1}}} = \dfrac{{\left| q \right|U}}{{{m_1}d}} = \dfrac{1}{{50}}.\dfrac{{100}}{{0,05}} = 40\left( {m/{s^2}} \right)\\{a_2} = \dfrac{{ - {F_2}}}{{{m_2}}} = \dfrac{{ - \left| q \right|E}}{{{m_2}}} = \dfrac{{ - \left| q \right|U}}{{{m_2}d}} =  - \dfrac{3}{{50}}.\dfrac{{100}}{{0,05}} =  - 120\left( {m/{s^2}} \right)\end{array} \right.\).

+ Quãng đường đi được của mỗi hạt khi đến gặp nhau: \(\left\{ \begin{array}{l}{s_1} = \dfrac{1}{2}{a_1}{t^2} = 20{t^2}\\{s_2} = \dfrac{1}{2}\left| {{a_2}} \right|{t^2} = 60{t^2}\end{array} \right.\)

+ Khi hai vật gặp nhau thì:

\(\begin{array}{l}d = {s_1} + {s_2} \leftrightarrow 20{t^2} + 60{t^2} = 0,05\\ \to t = 0,025{\rm{s}}\end{array}\) 

+ Ta có, các lực tác dụng lên hạt bụi gồm lực điện và trọng lực

Hạt bụi nằm lơ lửng (tức là cân bằng) ta có các lực tác dụng lên hạt bụi: \(\overrightarrow {{F_d}}  + \overrightarrow P  = \overrightarrow 0 \)

Hay \({F_d} = P \Leftrightarrow qE = mg\)

\( \Rightarrow q = \dfrac{{mgd}}{U}\)

Ta suy ra, số hạt electron thừa trong hạt bụi là: \(n = \dfrac{q}{{\left| e \right|}} = \dfrac{{mgd}}{{U\left| e \right|}} = \dfrac{{{{10}^{ - 7}}{{.10}^{ - 3}}.10.\left( {0,{{5.10}^{ - 2}}} \right)}}{{31,25.1,{{6.10}^{ - 19}}}} = {10^6}\)

+ Biểu thức định luật II Niu-tơn: \(\overrightarrow F  + \overrightarrow P  = m\overrightarrow a \)  (1)

Chọn chiều dương là chiều chuyển động của vật, ta có (1) tương đương với \(P - F = ma\)

+ Khi mất bớt đi một nửa điện tích thì F giảm đi một nửa nên \(P > F\)

\( \Rightarrow \) hạt sẽ chuyển động đi xuống nhanh nhần đều với gia tốc \(a = \dfrac{{P - F}}{m}\)

\(a = \dfrac{{mg - \dfrac{q}{2}E}}{m} = \dfrac{{mg - \dfrac{{mg}}{2}}}{m} = \dfrac{g}{2} = 5m/{s^2}\)

Vậy, nếu hạt bụi mất đi một nửa số electron có thừa thì hạt bụi sẽ chuyển động nhanh dần đều đi xuống với gia tốc \(a = 5m/{s^2}\)

Khi electron chuyển động từ bản này đến bản kia, thì nó chịu tác dụng của ngoại lực là lực điện trường.

+ Theo định lí động năng, ta có: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = qE{d_{12}}\)

\( \Rightarrow {d_{12}} = \dfrac{{ - {{\rm{W}}_{{d_1}}}}}{{qE}} = \dfrac{{ - 200.1,{{6.10}^{ - 19}}}}{{ - 1,{{6.10}^{ - 19}}.E}} = \dfrac{{200}}{E}\)

+ Để electron không đến được bản đối diện thì quãng đường nó đi được phải nhỏ hơn khoảng cách giữa hai bản này hay \({d_{12}} < d\)  (1)

Lại có: \(d = \dfrac{U}{E}\)  (2)

Từ (1) và (2) ta suy ra: \(\dfrac{{200}}{E} < \dfrac{U}{E} \Rightarrow U > 200V\)

+ Chọn hệ trục \(xOy\) như hình

+ Ta có, chuyển động của hạt được phân tích thành hai chuyển động.

- Theo phương ngang (Ox): hạt chuyển động thẳng đều với vận tốc ban đầu \({v_{0x}} = {v_0}cos\alpha \)

- Theo phương Oy: hạt chuyển động biến đổi đều với vận tốc đầu: \({v_{0y}} = {v_0}\sin \alpha \)

+ Phương trình vận tốc theo các trục: \(\left\{ \begin{array}{l}{v_x} = {v_0}cos\alpha \\{v_y} = {v_0}\sin \alpha  + at\end{array} \right.\)

+ Vì khi ra khỏi điện trường, vận tốc có phương ngang nên thành phần \({v_y} = 0\) do đó ta có:

\({v_0}\sin \alpha  + at = 0 \Rightarrow t = \dfrac{{ - {v_0}\sin \alpha }}{a}\)  (1)

+ Phương trình chuyển động theo phương Ox: \(x = \left( {{v_0}cos\alpha } \right)t\)

Khi ra khỏi điện trường thì \(x = L \Leftrightarrow \left( {{v_0}cos\alpha } \right)t = L\)  (2)

Từ (1) và (2), ta có: \(\left( {{v_0}cos\alpha } \right)\dfrac{{ - {v_0}\sin \alpha }}{a} = L\)  (3)

+ Mặt khác, ta có gia tốc của electron khi chuyển động trong điện trường: \(a = \dfrac{{ - F}}{m} = \dfrac{{ - \left| q \right|E}}{m} = \dfrac{{ - \left| q \right|U}}{{md}}\) (4)

Từ (3) và (4), ta có:

\(\eqalign{
& \left( {{v_0}cos\alpha } \right){{ - {v_0}\sin \alpha } \over {{{ - \left| q \right|U} \over {md}}}} = L \cr
& \Rightarrow U = {{mdv_0^2.\sin 2\alpha } \over {2\left| q \right|L}} = {{\left( {9,{{1.10}^{ - 31}}} \right).\left( {0,01} \right).{{\left( {2,{{5.10}^7}} \right)}^2}.\sin {{30}^0}} \over 2.{1,{{6.10}^{ - 19}}.0,05}} = 177,7V \cr} \)

Các lực tác dụng lên hạt bụi gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \)

Điều kiện cân bằng của hạt bụi: \(\overrightarrow F  + \overrightarrow P  = 0 \to F = P \leftrightarrow qE = mg \to q = \frac{{mg}}{E}\)

Mặt khác: \(E = \frac{U}{d} \to q = \frac{{mg}}{{\frac{U}{d}}} = \frac{{mgd}}{U}\)

Áp dụng cho lúc đầu và lúc sau, ta có: \(\left\{ \begin{array}{l}{q_1} = \frac{{mg{\rm{d}}}}{U}\\{q_2} = \frac{{mg{\rm{d}}}}{{U + \Delta U}}\end{array} \right.\)

\( \to \Delta q = {q_1} - {q_2} = mg{\rm{d}}\left( {\frac{1}{U} - \frac{1}{{U + \Delta U}}} \right) = {10^{ - 11}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{.10}}{\rm{.0,005}}{\rm{.}}\left( {\frac{1}{{306,3}} - \frac{1}{{306,3 + 34}}} \right) = 1,{63.10^{ - 19}}C\)

Lực tác dụng vào hạt bụi: \(\overrightarrow P ;\overrightarrow {{F_d}} \)

Hạt bụi cân bằng: \(\overrightarrow P  + \overrightarrow {{F_d}}  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow P  \uparrow  \downarrow \overrightarrow {{F_d}} \,\,\left( 1 \right)\\P = {F_d}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

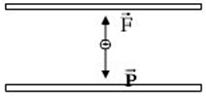
Từ (1) \( \Rightarrow \overrightarrow {{F_d}} \) hướng lên và cùng chiều \(\overrightarrow E \)\( \Rightarrow q > 0\)

Giải (2) ta có:

\(mg = \left| q \right|E \Rightarrow \left| q \right| = \dfrac{{mg}}{E} = \dfrac{{{{5.10}^{ - 9}}.10}}{{2000}} = 2,{5.10^{ - 11}}C\)

\( \Rightarrow q = 2,{5.10^{ - 11}}C\)

Hai điện tích trái dấu → chúng chuyển động ngược chiều

→ điện tích \({q_2}\) chuyển động ngược chiều kim đồng hồ

Bán kính quỹ đạo chuyển động của điện tích là: \(R = \dfrac{{mv}}{{\left| q \right|B}} \Rightarrow R \sim \dfrac{1}{{\left| q \right|}}\)

 Ta có: \(\dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = 4 \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{1}{4} \Rightarrow {R_2} = 4{R_1} = 4.4 = 16\,\,\left( {cm} \right)\)

Ta có:

Gia tốc:

\(a =  - \dfrac{{qE}}{m} =  - \dfrac{{1,{{6.10}^{ - 19}}.3000}}{{1,{{67.10}^{ - 27}}}} =  - 2,{87.10^{ - 11}}\) (dấu “-” do proton chuyển động ngược chiều \(\overrightarrow E \))

Áp dụng công thức độc lập với thời gian:

\({v^2} - v_0^2 = 2{\rm{a}}s \Leftrightarrow v = \sqrt {2.( - 2,{{87.10}^{11}}).0,03 + {{\left( {{{4.10}^5}} \right)}^2}}  = 3,{78.10^5}m/s\)

Khảo sát chuyển động của electron gồm 2 chuyển động:

+ Chuyển động vuông góc với đường sức là chuyển động thẳng đều => Phương trình chuyển động là: x = v.t

=> Thời gian đi đoạn đường 5cm là:

\(t = \dfrac{s}{v} = \dfrac{{0,05}}{{{{3.10}^7}}} = 1,{67.10^{ - 9}}s\)

+ Chuyển động dọc theo đường sức là chuyển động nhanh dần đều:

\(y = \dfrac{1}{2}a{t^2}\) với \(a = \dfrac{F}{m} = \dfrac{{qE}}{m} = \dfrac{{qU}}{{d.m}}\)

\(\begin{array}{l} \Rightarrow 0,0025 = 0,5.\dfrac{{1,{{6.10}^{ - 19}}.U}}{{0,02.9,{{1.10}^{ - 31}}}}.{\left( {1,{{67.10}^{ - 19}}} \right)^2}\\ \Rightarrow U \approx 204V\end{array}\)

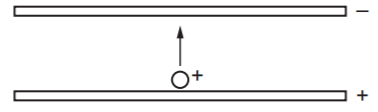
Nhận xét: điện trường giữa hai tấm kim lại tích điện trái dấu là điện trường đều có cường độ E

Lực điện tác dụng lên điện tích là:

\(F = \left| q \right|E = ma \Rightarrow a = \frac{{\left| q \right|E}}{m}\)

Chuyển động của điện tích có phương trình là:

\({v^2} - {v_0}^2 = 2ax \Rightarrow {v^2} = 2ax = 2\frac{{\left| q \right|E}}{m}x\)

Động năng của hạt là:

\({E_k} = \frac{1}{2}m{v^2} = \frac{1}{2}.m.2\frac{{\left| q \right|E}}{m}x = \left| q \right|Ex\)

→ Đồ thị động năng E_k theo quãng đường x là đường thẳng đi qua gốc tọa độ

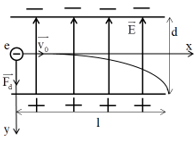
Gia tốc của electron là: \(a = \dfrac{{{F_d}}}{m} = \dfrac{{e.E}}{m} = \dfrac{{e.U}}{{m.d}}\)

Gia tốc theo phương Ox là: \({a_x} = 0\)

Gia tốc theo phương Oy là: \({a_y} = \dfrac{{eU}}{{md}}\)

Vận tốc theo phương Ox và Oy là:

\(\left\{ \begin{array}{l}{v_x} = {v_0}\\{v_y} = {v_{0y}} + {a_y}.t = \dfrac{{eU}}{{md}}.t\end{array} \right.\)

Phương trình chuyển động của electron theo phương Ox và Oy là:

\(\left\{ \begin{array}{l}x = {x_0} + {v_{0x}}t + \dfrac{1}{2}{a_x}.{t^2} = {v_0}.t \Rightarrow t = \dfrac{x}{{{v_0}}}\\y = {y_0} + {v_{0y}}.t + \dfrac{1}{2}{a_y}{t^2} = \dfrac{1}{2}.\dfrac{{eU}}{{md}}{t^2} = \dfrac{{eU}}{{2md.{v_0}^2}}.{x^2}\end{array} \right.\)

Thay số ta có:

\(2,{5.10^{ - 3}} = \dfrac{{1,{{6.10}^{ - 19}}.U}}{{2.9,{{1.10}^{ - 31}}.0,02.{{\left( {{{3.10}^7}} \right)}^2}}}.0,{05^2} \Rightarrow U = 204,75\,\,\left( V \right)\)