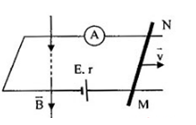
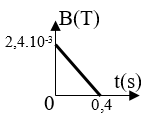
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E{\rm{ }} = {\rm{ }}1,5V\), điện trở trong \(r = 0,1\Omega \), thanh MN có chiều dài \(1m\) có điện trở \(R = 2,9\Omega \). Từ trường có phương thẳng đứng hướng xuống, vuông góc với mặt phẳng khung như hình vẽ. \(B = 0,1T\).

Khi MN di chuyển về phía bên phải với vận tốc \(v{\rm{ }} = {\rm{ }}3m/s\) sao cho hai đầu thanh MN luôn tiếp xúc hai thanh ray ? Tính độ lớn lực từ tác dụng lên thanh MN khi đó.
Trả lời bởi giáo viên
+ Dòng điện do nguồn tạo ra:
\(I = \dfrac{E}{{R + r}} = \dfrac{{1,5}}{{2,9 + 0,1}} = 0,5A\)
+ Khi thanh chuyển động về phía bên phải thì trong mạch có dòng điện cảm ứng có chiều từ M đến N và có độ lớn:
\({i_C} = \dfrac{{{e_C}}}{{R + r}} = \dfrac{{Blv}}{{R + r}} = \dfrac{{0,1.1.3}}{{2,9 + 0,1}} = 0,1A\)
Trong mạch có hai dòng điện là dòng do nguồn tạo ra và dòng cảm ứng do hiện tượng cảm ứng điện từ tạo ra, hai dòng này cùng chiều nên số chỉ của ampe kế là:
\({I_A} = I + {i_C} = 0,5 + 0,1 = 0,6A\)
+ Lực từ tác dụng lên thanh MN khi này là: \(F = B{I_A}l\sin {90^0} = 0,1.0,6.1 = 0,06N\)
Hướng dẫn giải:
+ Áp dụng định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\)
+ Áp dụng biểu thức tính cường độ dòng điện cảm ứng