Câu hỏi:
2 năm trước
Một thấu kính hội tụ có tiêu cự \(30 cm\). Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật \(40 cm\). Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có, vật AB qua thấu kính hội tụ cho ảnh ảo
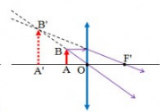
Do ảnh thu được là ảnh ảo, nên ta có:
\(\dfrac{1}{f} = \dfrac{1}{d} - \dfrac{1}{{d'}}\) (1)
Theo đầu bài, ta có: \(\left\{ \begin{array}{l}f = 30cm\\d' - d = 40cm\end{array} \right.\)
Thay vào (1), ta được:
\(\begin{array}{l}\dfrac{1}{{30}} = \dfrac{1}{d} - \dfrac{1}{{d + 40}}\\ \leftrightarrow d\left( {d + 40} \right) = 30\left( {d + 40} \right) - 30d\\ \leftrightarrow {d^2} + 40d - 1200 = 0\\ \to \left[ \begin{array}{l}d = 20cm\\d = - 60cm\end{array} \right.\end{array}\)
Hướng dẫn giải:
+ Cách vẽ ảnh của vật qua thấu kính hội tụ
+ Vận dụng công thức vị trí ảnh vật: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Trong đó:
- Vật thật, ảnh thật: \(d > 0,d' > 0\)
- Vật ảo: \(d < 0,d' < 0\)
