Một dây dẫn rất dài được căng thẳng, trong đó có một đoạn nhỏ được uốn thành vòng tròn bán kính 1,5cm trong đó chỗ bắt chéo hai dây không nối với nhau (như hình dưới). Cho dòng điện cường độ \(I = 3A\) chạy trong dây dẫn. Xác định véc tơ cảm ứng từ tại tâm O của vòng dây.
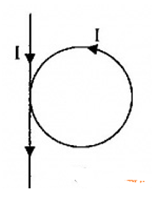
Gọi \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ gây bởi phần dòng điện thẳng dài và phần dòng điện tròn tại tâm O.
+ Dựa vào quy tắc nắm bàn tay phải, ta suy ra véc tơ \(\overrightarrow {{B_1}} \) có chiều từ trong ra, véc tơ \(\overrightarrow {{B_2}} \) cũng hướng từ trong ra ngoài
Ta có: \(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}\dfrac{I}{R} = {2.10^{ - 7}}\dfrac{3}{{1,{{5.10}^{ - 2}}}} = {4.10^{ - 5}}T\\{B_2} = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}\dfrac{3}{{1,{{5.10}^{ - 2}}}} = 12,{57.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \uparrow \uparrow \overrightarrow {{B_2}} \Rightarrow B = {B_1} + {B_2}\)
\(B = {B_1} + {B_2} = {4.10^{ - 5}} + 12,{57.10^{ - 5}} = 16,{57.10^{ - 5}}T\)
Dòng điện 2 A chạy trong dây dẫn thẳng dài. Cảm ứng từ tại điểm M cách dây dẫn 10 cm có độ lớn bằng bao nhiêu?
Cảm ứng từ tại điểm M là:
\(B = {2.10^{ - 7}}\dfrac{I}{r} = {2.10^{ - 7}}.\dfrac{2}{{0,1}} = {4.10^{ - 6}}\,\,\left( T \right)\)
Độ lớn cảm ứng từ sinh bởi dòng điện chạy trong ống dây tròn không phụ thuộc
Độ lớn cảm ứng từ sinh ra bởi dòng điện chạy trong ống dây tròn phụ thuộc: cường độ dòng điện, số vòng dây trên một mét chiều dài (hoặc số vòng dây của ống và chiều dài của ống); không phụ thuộc vào đường kính ống
Một dây dẫn thẳng dài đặt trong không khí có dòng điện với cường độ chạy qua. Độ lớn cảm ứng từ B do dòng điện này gây ra tại một điểm cách dây một đoạn được tính bởi công thức:
Độ lớn cảm ứng từ B do dòng điện thẳng dài gây ra tại một điểm cách dây một đoạn được tính bởi công thức: \(B = {2.10^{ - 7}}\dfrac{I}{r}\)
Một ống hình trụ dài \(0,5\,\,m\), đường kính \(16\,\,cm\). Một dây dẫn dài \(10\,\,m\), được quấn quanh ống dây với các vòng khít nhau cách điện với nhau, cho dòng điện chạy qua mỗi vòng là \(100\,\,A\). Cảm ứng từ trong lòng ống dây có độ lớn
Chu vi ống dây là: \(C = \pi d = \pi .0,16\,\,\left( m \right)\)
Số vòng dây trên \(1m\) chiều dài ống dây là:
\(n = \dfrac{L}{{C.{\rm{l}}}} = \dfrac{{10}}{{0,16\pi .0,5}} = \dfrac{{125}}{\pi }\,\,\left( {vong/m} \right)\)
Độ lớn cảm ứng từ trong lòng ống dây là:
\(B = 4\pi {.10^{ - 7}}nI = 4\pi {.10^{ - 7}}.\dfrac{{125}}{\pi }.100 = {5.10^{ - 3}}\,\,\left( T \right)\)
Một sợi dây đồng có bán kính 0,5mm. Dùng sợi dây này để cuốn một ống dây dài 20cm. Cho dòng điện có cường độ 4A chạy qua ống dây. Hãy xác định từ trường bên trong ống dây?
Hướng dẫn giải:
+ Gọi N – số vòng dây phải cuốn trên ống dây
Ta có, đường kính của dây cuốn chính là bề dày một vòng cuốn
=> Để cuốn hết chiều dài ống dây \(l\) thì phải cần N vòng cuốn, nên ta có:
\(Nd = l \Rightarrow \frac{N}{l} = \frac{1}{d} = \frac{1}{{2R}}\)
=> mật độ vòng dây: \(n = \frac{1}{{2R}} = \frac{1}{{2.0,{{5.10}^{ - 3}}}} = 1000\) (vòng/m)
+ Ta có: Cảm ứng từ \(B = 4\pi {.10^{ - 7}}nI = 4\pi {.10^{ - 7}}.1000.5 = 5,{03.10^{ - 3}}T\)
Tại sao tâm của vòng dây tròn có dòng điện cường độ 5A cảm ứng từ được đo là 31,4.10-6T. Đường kính của vòng dây điện đó là
Cách giải :
Áp dụng công thúc tính cảm ứng từ B tại tâm của vòng dây tròn ta có:
\(B = 2\pi {.10^{ - 7}}\frac{I}{R} \Rightarrow R = 2\pi {.10^{ - 7}}\frac{I}{B} = 2.\pi {.10^{ - 7}}\frac{5}{{31,{{4.10}^{ - 6}}}} = 0,1m = 10cm \Rightarrow d = 2.R = 20cm\)
Vậy đường kính của dây điện là 20 cm
Cảm ứng từ tại điểm \(M\) cách dây dẫn thẳng dài mang dòng điện \(I\) một khoảng \(r\) được tính bởi công thức
Cảm ứng từ tại điểm \(M\) cách dây dẫn thẳng dài mang dòng điện \(I\) một khoảng \(r\) được tính bởi công thức:
\(B = {2.10^{ - 7}}.\dfrac{I}{r}\)
Hai dây dẫn uốn thành 2 vòng tròn, được ghép đồng tâm như hình vẽ. Vòng thứ nhất có bán kính \({R_1} = 50cm\), mang dòng điện \({I_1} = 10A\), vòng thứ 2 có bán kính \({R_2} = 30cm\), mang dòng điện \({I_2} = 5A\). Xác định cảm ứng từ tại tâm của 2 vòng dây
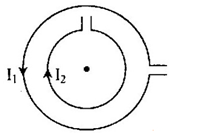
+ Gọi \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ do dòng điện tròn \({I_1}\) và \({I_2}\) gây ra tại tâm O.
+ Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) từ trong ra ngoài, và \(\overrightarrow {{B_2}} \) có chiều từ ngoài vào trong
\( \Rightarrow \overrightarrow {{B_1}} \uparrow \downarrow \overrightarrow {{B_2}} \Rightarrow B = \left| {{B_1} - {B_2}} \right|\)
+ Ta có: \(\left\{ \begin{array}{l}{B_1} = 2\pi {.10^{ - 7}}\dfrac{{{I_1}}}{{{R_1}}} = 2\pi {.10^{ - 7}}.\dfrac{{10}}{{{{50.10}^{ - 2}}}} = 4\pi {.10^{ - 6}}T\\{B_2} = 2\pi {.10^{ - 7}}\dfrac{{{I_2}}}{{{R_2}}} = 2\pi {.10^{ - 7}}\dfrac{5}{{{{30.10}^{ - 2}}}} = \dfrac{{10\pi }}{3}{.10^{ - 6}}T\end{array} \right.\)
\( \Rightarrow B = {B_1} - {B_2} = 4\pi {.10^{ - 6}} - \dfrac{{10\pi }}{3}{.10^{ - 6}} = \dfrac{{2\pi }}{3}{.10^{ - 6}}T\)
Cảm ứng từ \(B\) của dòng điện thẳng gây ra tại điểm \(M\), cách dòng điện \(3\,\,cm\) bằng \(2,{4.10^{ - 5}}\,\,\left( T \right)\). Cường độ dòng điện chạy trong dây dẫn là:
Cảm ứng từ do dòng điện thẳng gây ra tại điểm \(M\) là:
\(B = {2.10^{ - 7}}\dfrac{I}{r} \Rightarrow 2,{4.10^{ - 5}} = {2.10^{ - 7}}.\dfrac{I}{{{{3.10}^{ - 2}}}} \Rightarrow I = 3,6\,\,\left( A \right)\)
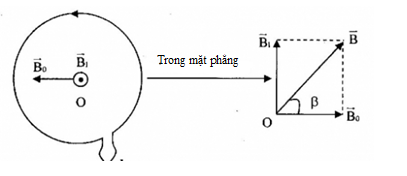
Vòng dây có bán kính \(\pi \left( {cm} \right)\), có dòng điện \(I = \dfrac{{\sqrt 3 }}{2}A\) đi qua và đặt song song với đường cảm ứng từ của một từ trường đều có \({B_0} = {10^{ - 5}}T\). Xác định giá trị của véc tơ cảm ứng từ tại tâm vòng dây.
Gọi \(\overrightarrow {{B_1}} \) là cảm ứng từ do dòng điện tròn gây ra tại tâm O.
Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) vuông góc với \(\overrightarrow {{B_0}} \)
Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) vuông góc với \(\overrightarrow {{B_0}} \)
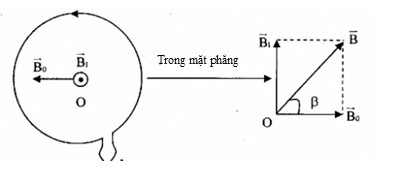
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_0}} \)
Ta có:
\({B_1} = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}\dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\pi {{.10}^{ - 2}}}} = \sqrt 3 {.10^{ - 5}}T\)
+ Từ hình, ta có:
\(\begin{array}{l}\tan \beta = \dfrac{{{B_1}}}{{{B_0}}} = \dfrac{{\sqrt 3 {{.10}^{ - 5}}}}{{{{10}^{ - 5}}}} = \sqrt 3 \\ \Rightarrow \beta = {60^0}\end{array}\)
=> Véc tơ cảm ứng từ tại tâm vòng dây hợp với véc tơ cảm ứng từ \(\overrightarrow {{B_0}} \) của từ trường đều một góc \({60^0}\).
Vòng dây có bán kính \(\pi \left( {cm} \right)\), có dòng điện \(I = \dfrac{{\sqrt 3 }}{2}A\) đi qua và đặt song song với đường cảm ứng từ của một từ trường đều có \({B_0} = {10^{ - 5}}T\). Xác định giá trị của véc tơ cảm ứng từ tại tâm vòng dây.
Gọi \(\overrightarrow {{B_1}} \) là cảm ứng từ do dòng điện tròn gây ra tại tâm O.
Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) vuông góc với \(\overrightarrow {{B_0}} \)
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_0}} \)
Ta có:
\({B_1} = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}\dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\pi {{.10}^{ - 2}}}} = \sqrt 3 {.10^{ - 5}}T\)
\(\begin{array}{l}\overrightarrow {{B_1}} \bot \overrightarrow {{B_0}} \\ \Rightarrow B = \sqrt {B_1^2 + B_0^2} = \sqrt {{{\left( {\sqrt 3 {{.10}^{ - 5}}} \right)}^2} + {{\left( {{{10}^{ - 5}}} \right)}^2}} = {2.10^{ - 5}}T\end{array}\)
Vòng dây có bán kính \(\pi \left( {cm} \right)\), có dòng điện \(I = \dfrac{{\sqrt 3 }}{2}A\) đi qua và đặt song song với đường cảm ứng từ của một từ trường đều có \({B_0} = {10^{ - 5}}T\). Véc tơ cảm ứng từ tại tâm vòng dây hợp với véc tơ cảm ứng từ \(\overrightarrow {{B_0}} \) của từ trường đều một góc bao nhiêu?
Gọi \(\overrightarrow {{B_1}} \) là cảm ứng từ do dòng điện tròn gây ra tại tâm O.
Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) vuông góc với \(\overrightarrow {{B_0}} \)
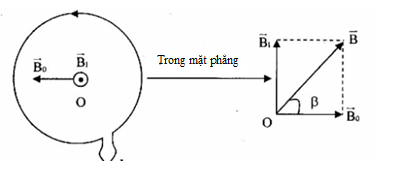
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_0}} \)
Ta có:
\({B_1} = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}\dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\pi {{.10}^{ - 2}}}} = \sqrt 3 {.10^{ - 5}}T\)
+ Từ hình, ta có:
\(\begin{array}{l}\tan \beta = \dfrac{{{B_1}}}{{{B_0}}} = \dfrac{{\sqrt 3 {{.10}^{ - 5}}}}{{{{10}^{ - 5}}}} = \sqrt 3 \\ \Rightarrow \beta = {60^0}\end{array}\)
=> Véc tơ cảm ứng từ tại tâm vòng dây hợp với véc tơ cảm ứng từ \(\overrightarrow {{B_0}} \) của từ trường đều một góc \({60^0}\).
Một dây đồng có đường kính \(d = 0,8mm\) có phủ sơn cách điện mỏng quấn quanh một hình trụ đường kính \(D = 5cm\) để tạo thành một ống dây. Khi nối ống dây với nguồn \(E = 4V,r = 0,5\Omega \) thì cảm ứng từ trong lòng ống dây là \(B = 5\pi {.10^{ - 4}}T\) . Xác định cường độ dòng điện trong ống dây?
Ta có:
+ Mật độ vòng dây: \(n = \dfrac{1}{d} = \dfrac{1}{{0,{{8.10}^{ - 3}}}} = 1250\) (vòng/m)
+ Cảm ứng từ: \(B = 4\pi {.10^{ - 7}}nI\)
Ta suy ra, cường độ dòng điện: \(I = \dfrac{B}{{4\pi {{.10}^{ - 7}}n}} = \dfrac{{5\pi {{.10}^{ - 4}}}}{{4\pi {{.10}^{ - 7}}.1250}} = 1A\)
Một dây đồng có đường kính \(d = 0,8mm\) có phủ sơn cách điện mỏng quấn quanh một hình trụ đường kính \(D = 5cm\) để tạo thành một ống dây. Khi nối ống dây với nguồn \(E = 4V,r = 0,5\Omega \) thì cảm ứng từ trong lòng ống dây là \(B = 5\pi {.10^{ - 4}}T\) . Xác định chiều dài ống dây, biết điện trở suất của dây cuốn là \(\rho = 1,{76.10^{ - 8}}\Omega m\)
Ta có:
+ Mật độ vòng dây: \(n = \dfrac{1}{d} = \dfrac{1}{{0,{{8.10}^{ - 3}}}} = 1250\) (vòng/m)
+ Cảm ứng từ: \(B = 4\pi {.10^{ - 7}}nI\)
Ta suy ra, cường độ dòng điện: \(I = \dfrac{B}{{4\pi {{.10}^{ - 7}}n}} = \dfrac{{5\pi {{.10}^{ - 4}}}}{{4\pi {{.10}^{ - 7}}.1250}} = 1A\)
+ Lại có \(I = \dfrac{E}{{R + r}} \Rightarrow R = \dfrac{E}{I} - r = \dfrac{4}{1} - 0,5 = 3,5\Omega \)
+ Chiều dài dây cuốn: \(l = \dfrac{{RS}}{\rho } = \dfrac{{R\left( {\pi \dfrac{{{d^2}}}{4}} \right)}}{\rho } = \dfrac{{3,5.\left( {\pi \dfrac{{{{\left( {0,{{8.10}^{ - 3}}} \right)}^2}}}{4}} \right)}}{{1,{{76.10}^{ - 8}}}} = 99,96m\)
Một dây đồng có đường kính \(d = 0,8mm\) có phủ sơn cách điện mỏng quấn quanh một hình trụ đường kính \(D = 5cm\) để tạo thành một ống dây. Khi nối ống dây với nguồn \(E = 4V,r = 0,5\Omega \) thì cảm ứng từ trong lòng ống dây là \(B = 5\pi {.10^{ - 4}}T\) . Xác định số vòng dây, biết điện trở suất của dây cuốn là \(\rho = 1,{76.10^{ - 8}}\Omega m\)
Ta có:
+ Mật độ vòng dây: \(n = \dfrac{1}{d} = \dfrac{1}{{0,{{8.10}^{ - 3}}}} = 1250\) (vòng/m)
+ Cảm ứng từ: \(B = 4\pi {.10^{ - 7}}nI\)
Ta suy ra, cường độ dòng điện: \(I = \dfrac{B}{{4\pi {{.10}^{ - 7}}n}} = \dfrac{{5\pi {{.10}^{ - 4}}}}{{4\pi {{.10}^{ - 7}}.1250}} = 1A\)
+ Lại có \(I = \dfrac{E}{{R + r}} \Rightarrow R = \dfrac{E}{I} - r = \dfrac{4}{1} - 0,5 = 3,5\Omega \)
+ Chiều dài dây cuốn: \(l = \dfrac{{RS}}{\rho } = \dfrac{{R\left( {\pi \dfrac{{{d^2}}}{4}} \right)}}{\rho } = \dfrac{{3,5.\left( {\pi \dfrac{{{{\left( {0,{{8.10}^{ - 3}}} \right)}^2}}}{4}} \right)}}{{1,{{76.10}^{ - 8}}}} = 99,96m\)
+ Số vòng dây: \(N = \dfrac{l}{{\pi D}} = \dfrac{{99,96}}{{\pi .0,05}} = 636,36\) vòng
Một ống dây hình trụ có chiều dài \(1,5m\) gồm \(4500\) vòng dây. Xác định cảm ứng từ trong lòng ống dây khi cho dòng điện \(I=5A\) chạy trong ống dây.
Ta có: \(B = 4\pi {.10^{ - 7}}\dfrac{{NI}}{l} = 4\pi {.10^{ - 7}}.\dfrac{{4500.5}}{{1,5}} = 6\pi {.10^{ - 3}}T\)
Một ống dây hình trụ có chiều dài 1,5m gồm 4500 vòng dây. Nếu ống dây tạo ra từ trường \(B = 0,03T\) thì cường độ dòng điện chạy trong ống dây có giá trị là:
Ta có: \(B = 4\pi {.10^{ - 7}}\dfrac{{NI}}{l}\)
Ta suy ra, cường độ dòng điện chạy trong ống dây: \(I = \dfrac{{Bl}}{{4\pi {{.10}^{ - 7}}N}} = \dfrac{{0,03.1,5}}{{4\pi {{.10}^{ - 7}}.4500}} = 7,96A\)
Một sợi dây đồng có bán kính \(0,5mm\). Dùng sợi dây này để cuốn một ống dây dài \(20cm\). Cho dòng điện có cường độ \(5A\) chạy qua ống dây. Hãy xác định từ trường bên trong ống dây?
+ Gọi N – số vòng dây phải cuốn trên ống dây
Ta có, đường kính của dây cuốn chính là bề dày một vòng cuốn
=> Để cuốn hết chiều dài ống dây \(l\) thì phải cần N vòng cuốn, nên ta có:
\(Nd = l \Rightarrow \dfrac{N}{l} = \dfrac{1}{d} = \dfrac{1}{{2R}}\)
=> mật độ vòng dây: \(n = \dfrac{1}{{2R}} = \dfrac{1}{{2.0,{{5.10}^{ - 3}}}} = 1000\) (vòng/m)
+ Ta có: Cảm ứng từ \(B = 4\pi {.10^{ - 7}}nI = 4\pi {.10^{ - 7}}.1000.5 = 6,{28.10^{ - 3}}T\)
Một khung dây dẫn tròn, cứng, đặt trong từ trường \(\overrightarrow B \) giảm dần đều như hình vẽ. Dòng điện cảm ứng trong khung có chiều
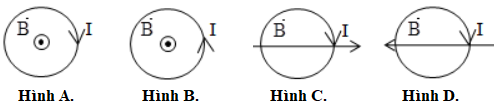
Ở hình B ta có cảm ứng từ \(\overrightarrow B \) có chiều hướng từ trong ra ngoài mặt phẳng hình vẽ.
Từ trường \(\overrightarrow B \) giảm dần đều \( \Rightarrow \overrightarrow {{B_C}} \uparrow \uparrow \vec B{\rm{ }}\)
\( \Rightarrow \overrightarrow {{B_C}} \) có chiều hướng từ trong ra ngoài.
Sử dụng quy tắc nắm tay phải ta xác định được chiều của cường độ dòng điện có chiều ngược chiều kim đồng hồ.
\( \Rightarrow \) Hình B đúng.

