Một khung dây tròn bán kính \(4\,\,cm\) gồm \(10\) vòng dây. Dòng điện chạy trong mỗi vòng có cường độ \(0,3\,\,A\). Tính cảm ứng từ tại tâm của khung.
Cảm ứng từ tại tâm khung dây là:
\(B = 2\pi {.10^{ - 7}}.\dfrac{{NI}}{R} = 2\pi {.10^{ - 7}}.\dfrac{{10.0,3}}{{0,04}} = 4,{7.10^{ - 5}}\,\,\left( T \right)\)
Biểu thức nào sau đây xác định cảm ứng từ của dòng điện thẳng dài đặt trong không khí:
Cảm ứng từ của dòng điện thẳng dài đặt trong không khí được xác định bởi biểu thức: \(B = {2.10^{ - 7}}\frac{I}{r}\)
Một dây dẫn thẳng dài có dòng điện chạy qua với cường độ I = 5A. Cảm ứng từ tại điểm M cách dây dẫn một đoạn r = 4cm có giá trị là:
Cảm ứng từ tại M là: \(B = {2.10^{ - 7}}\dfrac{I}{r} = {2.10^{ - 7}}\dfrac{5}{{{{4.10}^{ - 2}}}} = 2,{5.10^{ - 5}}\,T\)
Hai dây dẫn thẳng dài, đặt song song, cách nhau $10 cm$ trong không khí, có hai dòng điện ngược chiều, có cường độ $I_1= 6 A$; $I_2= 12 A$ chạy qua. Cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm $M$ cách dây dẫn mang dòng $I_1$ một đoạn $5 cm$ và cách dây dẫn mang dòng $I_2$ một đoạn $15 cm$ là bao nhiêu?
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B thì các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) có phương chiều như hình vẽ:
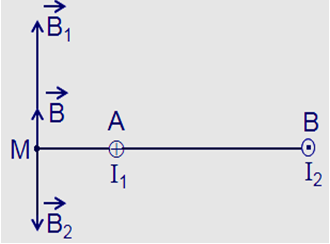
Có độ lớn: \({B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {\rm{ }}2,{4.10^{ - 5}}T;{\rm{ }}{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {\rm{ }}1,{6.10^{ - 5}}T.\)
Cảm ứng từ tổng hợp tại M là: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) cùng phương, ngược chiều và B1 > B2 nên \(\mathop B\limits^ \to \) cùng phương, chiều với \(\mathop {{B_1}}\limits^ \to \) và có độ lớn: B = B1 - B2 = 0,8.10-5 T
Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 10 cm trong không khí, có hai dòng điện cùng chiều, có cường độ I1 = 9 A; I2 = 16 A chạy qua. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách dây dẫn mang dòng I1 6 cm và cách dây dẫn mang dòng I2 8 cm?
- Bước 1:
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi vào tại B. Tam giác AMB vuông tại M. Các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \)có phương chiều như hình vẽ:
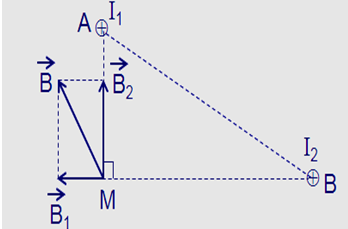
- Bước 2:
Có độ lớn: \({B_1} = {2.10^{ - 7}}\frac{{{I_1}}}{{AM}} = {3.10^{ - 5\,}}\,T,{B_2} = {2.10^{ - 7}}\frac{{{I_2}}}{{BM}} = {4.10^{ - 5}}\,T\)
- Bước 3:
Cảm ứng từ tổng hợp tại M là: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \) có phương chiều như hình vẽ và có độ lớn:
\(B = \sqrt {B_1^2 + B_2^2} = \sqrt {{{\left( {{{3.10}^{ - 5}}} \right)}^2} + {{\left( {{{4.10}^{ - 5}}} \right)}^2}} = {5.10^{ - 5}}\,T\)
Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau \(20 cm\) trong không khí, có hai dòng điện ngược chiều, cùng cường độ \({I_1} = {\rm{ }}{I_2} = {\rm{ }}9{\rm{ }}A\) chạy qua. Cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách hai dây như hình vẽ. Biết H cách đều 2 dây và \(MH = 30cm\).
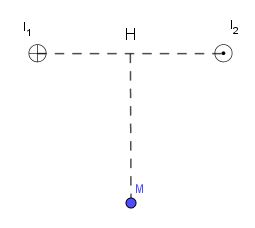
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B. Các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ $\mathop {{B_1}}\limits^ \to $ và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
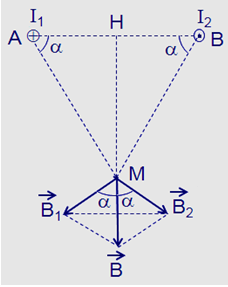
Có độ lớn: \({B_1} = {\rm{ }}{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}}\)
\(HM = 30cm, AB = 20cm\)
\(AM = \sqrt {A{H^2} + H{M^2}} = \sqrt {{{10}^2} + {{30}^2}} = 10\sqrt {10} cm\)
Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(\begin{array}{l}B = {B_1}cosa + {B_2}cosa = 2{B_1}cosa\\ = 2{B_1}\dfrac{{AH}}{{AM}} = {2.2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}}.\dfrac{{AH}}{{AM}}\\ = {2.2.10^{ - 7}}\dfrac{{9.0,1}}{{{{\left( {0,1\sqrt {10} } \right)}^2}}} = {3,6.10^{ - 6}}T\end{array}\)
Hai dây đẫn thẳng dài vô hạn, đặt song song trong không khí cách nhau một đoạn $d = 12 cm$ có các dòng điện cùng chiều $I_1 =I_2 =I = 10 A$ chạy qua. Một điểm $M$ cách đều mỗi dây dẫn một đoạn $x$. $x$ bằng bao nhiêu để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại?
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng $I_1$ đi vào tại $A$, dòng $I_2$ đi vào tại $B$. Các dòng điện $I_1$ và $I_2$ gây ra tại $M$ các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
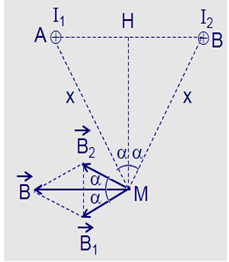
Có độ lớn: \({B_1} = {B_2} = {2.10^{ - 7}}\dfrac{I}{x}\).
Cảm ứng từ tổng hợp tại M là:
\(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(B = {B_1}cosa + {B_2}cosa = 2{B_1}cosa = 2{B_1}\dfrac{{HM}}{{AM}} = {2.2.10^{ - 7}}\dfrac{I}{x}\dfrac{{\sqrt {{x^2} - {{\left( {\dfrac{d}{2}} \right)}^2}} }}{x} = {4.10^{ - 7}}I\sqrt {\dfrac{1}{{{x^2}}} - \dfrac{{{d^2}}}{{4{x^4}}}} \)
Nhận thấy, B đạt cực đại khi \(\dfrac{1}{{{x^2}}} - \dfrac{{{d^2}}}{{4{x^4}}}\) đạt cực đại
Ta có: \(\dfrac{1}{{{x^2}}} - \dfrac{{{d^2}}}{{4{x^4}}} = \dfrac{4}{{{d^2}}}\dfrac{{{d^2}}}{{4{x^2}}}\left( {1 - \dfrac{{{d^2}}}{{4{x^2}}}} \right)\)
Do \(d < x \to 1 - \dfrac{{{d^2}}}{{4{x^2}}} > 0\)
Áp dụng BĐT cosi ta có: \(\dfrac{{{d^2}}}{{4{{\rm{x}}^2}}}(1 - \dfrac{{{d^2}}}{{4{{\rm{x}}^2}}}) \le \dfrac{{{{\left( {\dfrac{{{d^2}}}{{4{{\rm{x}}^2}}} + 1 - \dfrac{{{d^2}}}{{4{{\rm{x}}^2}}}} \right)}^2}}}{4} = \dfrac{1}{4}\)
Dấu “ = ” xảy ra khi: \(\dfrac{{{d^2}}}{{4{{\rm{x}}^2}}} = (1 - \dfrac{{{d^2}}}{{4{{\rm{x}}^2}}}) \to {x^2} = \dfrac{{{d^2}}}{2} \to x = \dfrac{d}{{\sqrt 2 }} = \dfrac{{12}}{{\sqrt 2 }} = 6\sqrt 2 cm\)
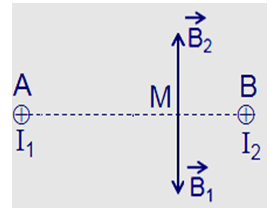
Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 15 cm trong không khí, có hai dòng điện cùng chiều, có cường độ I1 = 10 A, I2 = 5 A chạy qua. Điểm M cách A và B một khoảng bằng bao nhiêu mà tại đó cảm ừng từ tổng hợp do hai dòng điện này gây ra bằng 0?
- Bước 1:
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi vào tại B. Các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \)và \(\mathop {{B_2}}\limits^ \to \).
- Bước 2:
Để cảm ứng từ tổng hợp tại M bằng 0 thì \(\mathop B\limits^ \to = \mathop{{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to = 0 \to \mathop{{B_1}}\limits^ \to = - \mathop {{B_2}}\limits^ \to \) tức là \(\mathop{{B_1}}\limits^ \to \)và \(\mathop {{B_2}}\limits^ \to \)phải cùng phương, ngược chiều và bằng nhau về độ lớn.
Để thỏa mãn các điều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm trong đoạn thẳng AB.
- Bước 3:
Với B1 = B2 thì \({2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{AB - AM}}\) \( \to AM = \dfrac{{AB.{I_1}}}{{{I_1} + {I_2}}} = \dfrac{{15.10}}{{10 + 5}} = 10cm,MB = 15 - 10 = 5cm\)
Vậy điểm M phải nằm trên đường thẳng cách dây dẫn mang dòng I1 10 cm và cách dây dẫn mang dòng I2 5 cm
Hai dây dẫn thẳng, rất dài, đặt trong không khí, trùng với hai trục tọa độ vuông góc $xOy$. Dòng điện qua dây $Ox$ chạy cùng chiều với chiều dương của trục tọa độ và có cường độ $I_1= 2A$ , dòng điện qua dây $Oy$ chạy ngược chiều với chiều dương của trục tọa độ và có cường độ $I_2= 3 A$. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm $M$ có tọa độ $x = 4 cm$ và $y = -2 cm$
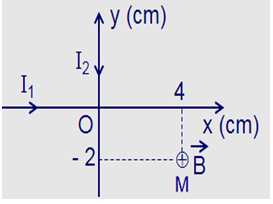
Dòng I1 gây ra tại $M$ véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) vuông góc với mặt phẵng $xOy$, hướng từ ngoài vào, có độ lớn:
\({B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{|y|}} = {\rm{ }}{2.10^{ - 5}}T\)
Dòng I2 gây ra tại A véc tơ cảm ứng từ \(\mathop {{B_2}}\limits^ \to \) vuông góc với mặt phẵng xOy, hướng từ trong ra, có độ lớn:
\({B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{|x|}} = {\rm{ }}1,{5.10^{ - 5}}T\)
Cảm ứng từ tổng hợp tại A là \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \).
Vì \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) cùng phương, ngược chiều và B1 > B2 nên \(\mathop B\limits^ \to \) cùng phương, cùng chiều với\(\mathop {{B_1}}\limits^ \to \) và có độ lớn
B = B1 – B2 = 0,5.10-5 T.
Biểu thức nào sau đây xác định cảm ứng từ của dòng điện tròn đặt trong không khí:
Cảm ứng từ của dòng điện tròn đặt trong không khí được xác định bởi biểu thức: \(B = 2\pi {.10^{ - 7}}\frac{I}{R}\)
Một vòng dây tròn đặt trong chân không có bán kín R = 10 cm mang dòng điện I = 50 A. Độ lớn của véc tơ cảm ứng từ tại tâm vòng dây là:
Độ lớn cảm ứng từ tại tâm vòng dây \(B = 2\pi {.10^{ - 7}}\frac{I}{R} = \pi {.10^{ - 4}}T\)
Một dây dẫn thẳng, dài có vỏ bọc cách điện, ở khoảng giữa được uốn thành vòng tròn, bán kính R = 20 cm như hình vẽ. Dòng điện chạy qua dây dẫn có cường độ 5 A. Xác định cảm ứng từ tại tâm O của vòng tròn.
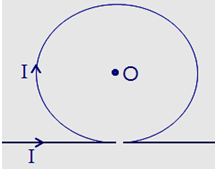
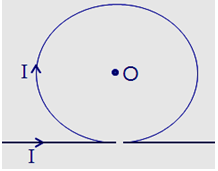
Dòng điện chạy trong vòng tròn gây ra tại tâm O cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) vuông góc với mặt phẳng hình vẽ, hướng từ ngoài vào và có độ lớn: \({B_1} = 2\pi {.10^{ - 7}}\frac{I}{R} = 15,{7.10^{ - 6}}T\)
Dòng điện chạy trong dây dẫn thẳng gây ra tại tâm O cảm ứng từ \(\mathop {{B_2}}\limits^ \to \) vuông góc với mặt phẳng hình vẽ, hướng từ trong ra và có độ lớn: \({B_2} = {2.10^{ - 7}}\frac{I}{R} = {5.10^{ - 6}}T\)
Cảm ứng từ tổng hợp tại O là \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \).
Vì \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \)cùng phương, ngược chiều và B1 > B2 nên \(\mathop B\limits^ \to \) cùng phương, cùng chiều với \(\mathop {{B_1}}\limits^ \to \) và có độ lớn B = B1 – B2 = 10,7.10-6 T.
Xác định cảm ứng từ tại tâm vòng tròn. Biết một sợi dây rất dài căng- thẳng. Ở khoảng giữa được uốn thành vòng tròn như hình. Bán kính vòng tròn R = 6cm, cường độ dòng điện chạy qua dây dẫn I = 3,75A.
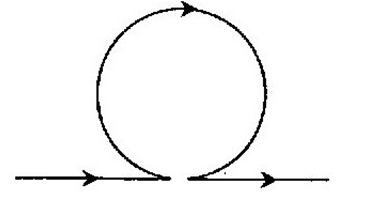
Gọi \(\overrightarrow {{B_1}} ;\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ gây bởi phần dòng điện thẳng dài và phần dòng điện tròn tại tâm O
\(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}\frac{I}{R} = {2.10^{ - 7}}\frac{{3,75}}{{0,06}} = 1,{25.10^{ - 5}}T\\{B_2} = 2\pi {.10^{ - 7}}\frac{I}{R} = 2\pi {.10^{ - 7}}\frac{{3,75}}{{0,06}} = 3,{93.10^{ - 5}}T\end{array} \right.\)
+ Dựa vào quy tắc nắm bàn tay phải ta suy ra véctơ \(\overrightarrow {{B_1}} \) có chiều từ trong ra, véctơ \(\overrightarrow {{B_2}} \) có chiều hướng từ ngoài vào trong
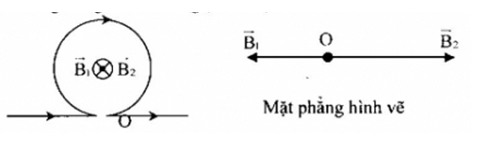
+ Cảm ứng từ tổng hợp tại tâm O: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \)
+ Vì \(\overrightarrow {{B_1}} ;\overrightarrow {{B_2}} \) ngược chiều và B2 > B1 nên véctơ cảm ứng từ tổng hợp \(\overrightarrow B \) có chiều là chiều của và có độ lớn: B = B2 - B1 = 2,68.10-5T
Hai dòng điện tròn có bán kính R = 10cm có tâm trùng nhau đặt vuông góc với nhau. Cường độ dòng điện trong hai dây \(I = {I_1} = {I_2} = \sqrt 2 \) . Cảm ứng từ tổng hợp tại tâm của hai vòng dây là:
- Bước 1:
Gọi \(\overrightarrow {{B_1}} ;\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ gây bởi các dòng điện tròn tại tâm O
Dựa vào quy tắc bàn tay phải, ta suy ra véctơ \(\overrightarrow {{B_1}} \) và véctơ \(\mathop {{B_2}}\limits^ \to \) có chiều như hình vẽ:
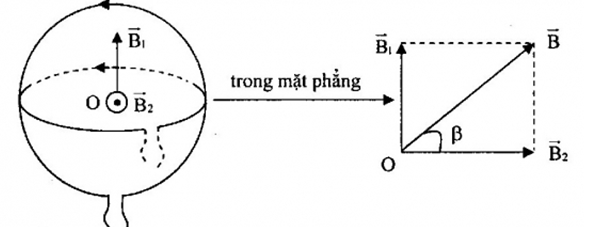
- Bước 2:
+ Vì: \(\left\{ \begin{array}{l}{I_1} = {I_2} = I\\{R_1} = {R_2} = R\end{array} \right. \to {B_1} = {B_2} = 2\pi {.10^{ - 7}}\frac{I}{R} = 2\sqrt 2 \pi {10^{ - 6}}T\)
+ Cảm ứng từ tổng hợp tại tâm O: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \)
+ Vì \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) vuông góc với nhau nên: \(B = \sqrt {B_1^2 + B_2^2} = \sqrt 2 {B_1} = \sqrt 2 .2\sqrt 2 \pi {.10^{ - 6}} = 4\pi {.10^{ - 6}}T\)
Một dây dẫn trong không khí được uốn thành vòng tròn , bán kính R = 0,1m có I = 3,2A chạy qua. Mặt phẳng vòng dây trùng với mặt phẳng kinh tuyến từ. Tại tâm vòng dây treo một kim nam châm nhỏ. Góc quay của kim nam châm khi ngắt dòng điện là bao nhiêu? Biết thành phần nằm ngang của cảm ứng từ trái đất có \({B_D} = 64\pi {.10^{ - 7}}\,T\), thành phần thẳng đứng không đáng kể
+ Cảm ứng từ do dòng điện tạo ra là: \({B_1} = 2\pi {.10^{ - 7}}\frac{I}{R} = 6,4\pi {.10^{ - 6}}\,T\)
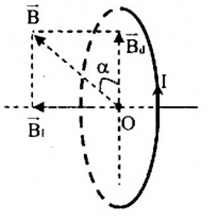
+ Cảm ứng từ tổng hợp của Trái Đất và dòng điện có phương tạo với thành phần nằm ngang của cảm ứng từ Trái Đất một góc α với: \(\tan \alpha = \frac{{{B_1}}}{{{B_D}}} = 1 \to \alpha = {45^0}\)
+ Khi tắt dòng điện, thì cảm ứng từ B1 mất đi, lúc này chỉ còn thành phần nằm ngang của từ trường Trái Đất nên kim nam châm sẽ đến trùng với phương thành phần nằm ngang Trái Đất, tức kim nam châm sẽ quay một góc 450
Biểu thức nào sau đây xác định cảm ứng từ của dòng điện trong ống dây:
Cảm ứng từ của dòng điện trong ống dây được xác định bởi biểu thức: \(B = 4\pi {.10^{ - 7}}\frac{N}{l}I\)
Một dây dẫn đường kính tiết diện $d = 0,5 mm$ được phủ một lớp sơn cách điện mỏng và quấn thành một ống dây, các vòng dây quấn sát nhau. Cho dòng điện có cường độ $I = 2 A$ chạy qua ống dây. Xác định cảm ứng từ tại một điểm trên trục trong ống dây.
Số vòng dây quấn sát nhau trên ống dây: $N = \dfrac{l}{d}$
Cảm ứng từ tại một điểm bên trong ống dây:
\(B = 4\pi {.10^{ - 7}}\dfrac{N}{l}I = 4\pi {.10^{ - 7}}\dfrac{{\frac{l}{d}}}{l}I = 4\pi {.10^{ - 7}}\dfrac{1}{d}I = 4\pi {.10^{ - 7}}\dfrac{1}{{0,{{5.10}^{ - 3}}}}.2 = {5.10^{ - 3}}T\)
Cho dòng điện cường độ I = 0,15 A chạy qua các vòng dây của một ống dây, thì cảm ứng từ bên trong ống dây là B = 35.10-5 T. Ống dây dài 50 cm. Số vòng dây của ống dây là:
Ta có: \(B = 4\pi {.10^{ - 7}}\frac{N}{l}I \to N = \frac{{lB}}{{4\pi {{.10}^{ - 7}}I}} = 928\) vòng
Dùng một dây đồng có phủ một lớp sơn cách điện mỏng, quấn quanh một hình trụ dài $L = 50 cm$, có đường kính $d = 4 cm$ để làm một ống dây. Sợi dây quấn ống dây có chiều dài \(l= 314 cm\) và các vòng dây được quấn sát nhau. Hỏi nếu cho dòng điện cường độ $I = 0,4 A$ chạy qua ống dây, thì cảm ứng từ bên trong ống dây bằng bao nhiêu?
Chu vi của mỗi vòng dây: $\pi d$, số vòng dây: \(N = \dfrac{l}{{\pi d}}\)
Cảm ứng từ bên trong ống dây:
\(\begin{array}{l}B = 4\pi {.10^{ - 7}}\dfrac{N}{L}I = 4\pi {.10^{ - 7}}\dfrac{{\dfrac{l}{{\pi d}}}}{L}I\\ = {4.10^{ - 7}}\dfrac{{l.I}}{{L.d}} = {4.10^{ - 7}}\dfrac{{{{314.10}^{ - 2}}.0,4}}{{0,5.0,04}} = 2,{5.10^{ - 5}}T\end{array}\)
Một dây dẫn được uốn thành một đa giác n cạnh đều nội tiếp trong một đường tròn bán kính R có dòng điện I chạy qua. Cảm ứng từ B tại tâm của đa giác Xét trường hợp \(n \to \infty \)
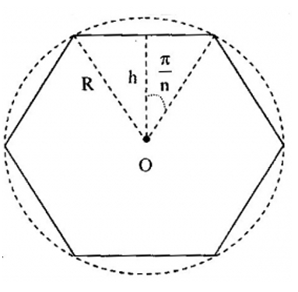
+ Cảm ứng từ do một cạnh của lục giác gây ra tại O có độ lớn:
\({B_1} = {10^{ - 7}}\frac{I}{h}2.\sin \frac{\pi }{n}\)
ta có: \(h = Rc{\rm{os}}\frac{\pi }{n} \to {B_1} = {10^{ - 7}}\frac{I}{{Rc{\rm{os}}\frac{\pi }{n}}}2.\sin \frac{\pi }{n} \to {B_1} = {10^{ - 7}}\frac{{2I}}{R}\tan \frac{\pi }{n}\)
+ Cảm ứng từ của n cạnh của lục giác gây ra tại O:
\(B = n{B_1} = {2.10^{ - 7}}\frac{{nI}}{R}\tan \frac{\pi }{n} \to B = 2\pi {.10^{ - 7}}\frac{I}{R}\frac{{\tan \frac{\pi }{n}}}{{\frac{\pi }{n}}}\)
Khi \(n \to \infty \) ta có: \(\frac{{\tan \frac{\pi }{n}}}{{\frac{\pi }{n}}} \to 1\) (Do: \(\mathop {\lim }\limits_{x \to \infty } \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{x} = 1 \to \mathop {\lim }\limits_{x \to \infty } \frac{{\tan x}}{x} = 1\)
=> \(B = 2\pi {.10^{ - 7}}\frac{I}{R}\)

