Vòng dây có bán kính \(\pi \left( {cm} \right)\), có dòng điện \(I = \dfrac{{\sqrt 3 }}{2}A\) đi qua và đặt song song với đường cảm ứng từ của một từ trường đều có \({B_0} = {10^{ - 5}}T\). Véc tơ cảm ứng từ tại tâm vòng dây hợp với véc tơ cảm ứng từ \(\overrightarrow {{B_0}} \) của từ trường đều một góc bao nhiêu?
Trả lời bởi giáo viên
Gọi \(\overrightarrow {{B_1}} \) là cảm ứng từ do dòng điện tròn gây ra tại tâm O.
Áp dụng quy tắc nắm bàn tay phải, ta suy ra chiều của \(\overrightarrow {{B_1}} \) vuông góc với \(\overrightarrow {{B_0}} \)
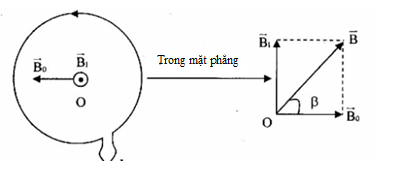
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_0}} \)
Ta có:
\({B_1} = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}\dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\pi {{.10}^{ - 2}}}} = \sqrt 3 {.10^{ - 5}}T\)
+ Từ hình, ta có:
\(\begin{array}{l}\tan \beta = \dfrac{{{B_1}}}{{{B_0}}} = \dfrac{{\sqrt 3 {{.10}^{ - 5}}}}{{{{10}^{ - 5}}}} = \sqrt 3 \\ \Rightarrow \beta = {60^0}\end{array}\)
=> Véc tơ cảm ứng từ tại tâm vòng dây hợp với véc tơ cảm ứng từ \(\overrightarrow {{B_0}} \) của từ trường đều một góc \({60^0}\).
Hướng dẫn giải:
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V)
+ Áp dụng biểu thức xác định cảm ứng từ của dòng điện tròn: \(B = 2\pi {.10^{ - 7}}\dfrac{I}{R}\)