Một mạch điện kín gồm hai nguồn điện \({E_1},{r_1}\) và \({E_2},{r_2}\) mắc nối tiếp với nhau, mạch ngoài chỉ có điện trở \(R\). Biểu thức cường độ dòng điện trong mạch là:
+ Suất điện động của bộ nguồn là: \({E_b} = {E_1} + {E_2}\)
+ Điện trở trong của bộ nguồn là: \({r_b} = {r_1} + {r_2}\)
+ Cường độ dòng điện trong mạch: \(I = \dfrac{{{E_b}}}{{{R+r_b}}} = \dfrac{{{E_1} + {E_2}}}{{R+{r_1} + {r_2}}}\)
Cho đoạn mạch như hình vẽ trong đó \({E_1} = 9V\), \({r_1} = 1,2\Omega \); \({E_2} = 3\left( V \right)\), \({r_2} = 0,4\Omega \). Điện trở \(R = 28,4\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch có chiều và độ lớn là:
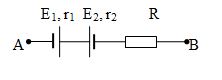
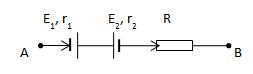
Giả sử dòng điện đi từ A sang B như hình vẽ khi đó E1 là nguồn điện, E2 là máy thu áp dụng định luật Ôm cho đoạn mạch chứa máy thu: \(I = \frac{{{{\rm{U}}_{{\rm{AB}}}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \frac{{6 + 9 - 3}}{{28,4 + 1,2 + 0,4}} = 0,4\left( A \right) > 0\)
=> Điều giả sử là đúng
=> chiều dòng điện đi theo chiều giả sử (chiều từ A sang B)
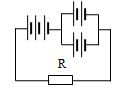
Cho mạch điện như hình vẽ. Mỗi pin có suất điện động \(E = 1,5V\), điện trở trong \(r = 1\Omega \). Điện trở mạch ngoài \(R = 3,5\Omega \). Cường độ dòng điện ở mạch ngoài là:
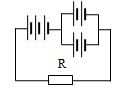
- Nguồn điện gồm 7 pin mắc như hình, đây là bộ nguồn gồm 3 pin ghép nối tiếp rồi lại ghép nối tiếp với một bộ khác gồm hai dãy mắc song song, mỗi dãy gồm hai pin mắc nối tiếp.
- Áp dụng công thức mắc nguồn thành bộ trong trường hợp mắc nối tiếp và mắc song song, ta tính được suất điện động và điện trở trong của bộ nguồn là: \({E_b} = 7,5V;{r_b} = 4\Omega \)
- Áp dụng công thức định luật Ôm cho toàn mạch \(I = \frac{{{E_b}}}{{R + {r_b}}} = \frac{{7,5}}{{3,5 + 4}} = 1A\)
Một ấm điện có hai dây dẫn \({R_1}\) và \({R_2}\) để đun nước. Nếu dùng dây \({R_1}\) thì nước trong ấm sẽ sôi sau thời gian \({t_1} = 10\) (phút). Còn nếu dùng dây \({R_2}\) thì nước sẽ sôi sau thời gian \({t_2} = 40\) (phút). Nếu dùng cả hai dây mắc song song thì nước sẽ sôi sau thời gian là bao nhiêu?
Một ấm điện có hai dây dẫn \({R_1}\) và \({R_2}\) để đun nước, trong cả 3 trường hợp nhiệt lượng mà nước thu vào đều như nhau.
- Khi dùng dây \({R_1}\) thì nước trong ấm sẽ sôi sau thời gian \({t_1} = 10\) (phút).
Nhiệt lượng dây \({R_1}\) toả ra trong thời gian đó là: \(Q = I_1^2{R_1}{t_1} = \dfrac{{{U^2}}}{{{R_1}}}{t_1}\)
- Khi dùng dây \({R_2}\) thì nước trong ấm sẽ sôi sau thời gian \({t_2} = 40\) (phút).
Nhiệt lượng dây \({R_2}\) toả ra trong thời gian đó là: \(Q = I_2^2{R_2}{t_2} = \dfrac{{{U^2}}}{{{R_2}}}{t_2}\)
- Khi dùng cả hai dây mắc song song thì sẽ sôi sau thời gian t
Nhiệt lượng dây toả ra trong thời gian đó là \(Q = \dfrac{{{U^2}}}{R}t\)
Với \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\)
Ta suy ra \(\dfrac{1}{t} = \dfrac{1}{{{t_1}}} + \dfrac{1}{{{t_2}}} = \dfrac{1}{{10}} + \dfrac{1}{{40}} \to t = 8\)(phút)
Cho mạch điện sau:
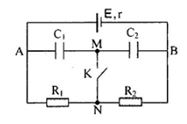
Biết $E{\rm{ }} = {\rm{ }}24V$, $r = 2\Omega $, ${R_1} = {R_2} = 5\Omega $, ${C_1} = {\rm{ }}{4.10^{ - 7}}F$,${C_2} = {\rm{ }}{6.10^{ - 7}}F$
Điện tích trên $2$ bản tụ điện khi $K$ đóng là?
Ta có: Dòng điện một chiều không qua tụ điện nên khi khóa K đóng - dòng điện chỉ chạy qua R1 và R2.
Dòng điện chạy trong mạch: \(I = \dfrac{E}{{{R_1} + {R_2} + r}} = \dfrac{{24}}{{5 + 5 + 2}} = 2(A)\)
+ Lúc này, tụ C1 // R1 và tụ C2 // R2, ta có: \(\left\{ \begin{array}{l}{U_{C1}} = {U_{R1}} = I{R_1} = 10V\\{U_{C2}} = {U_{R2}} = I{R_2} = 10V\end{array} \right.\)
Điện tích của các tụ lúc này: \(\left\{ \begin{array}{l}{Q_1} = {C_1}{U_{C1}} = {4.10^{ - 6}}C\\{Q_2} = {C_2}{U_{C2}} = {6.10^{ - 6}}C\end{array} \right.\)
Cho mạch điện như hình vẽ:
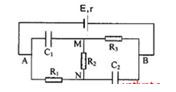
$E{\rm{ }} = {\rm{ }}12V$ , $r{\rm{ }} = {\rm{ }}2\Omega $ , ${R_1} = {\rm{ }}1\Omega $, ${R_2} = {\rm{ }}2\Omega $ , ${R_3} = {\rm{ }}3\Omega $ , ${C_1} = {\rm{ }}1\mu F$,${C_2} = {\rm{ }}2\mu F$.
Điện tích trên từng tụ điện là?
Ta có: Dòng điện một chiều không qua tụ nên mạch điện được vẽ lại như hình:
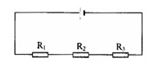
Tổng trở mạch ngoài: ${R_{ng}} = {\rm{ }}{R_1} + {\rm{ }}{R_2} + {\rm{ }}{R_3} = {\rm{ }}6\Omega $
Dòng điện qua mạch chính: \(I = \dfrac{E}{{{R_{ng}} + r}} = 1,5A\)
+ Hiệu điện thế giữa hai đầu tụ ${C_1}$là:
${U_{MA}} = {\rm{ }}{U_2} + {\rm{ }}{U_1} = {\rm{ }}I{\rm{ }}\left( {{R_2} + {\rm{ }}{R_1}} \right){\rm{ }} = {\rm{ }}4,5V$
=> Điện tích tụ ${C_1}$ tích được: ${Q_1} = {\rm{ }}{C_1}{U_{MA}} = 4,{5.10^{ - 6}} = {\rm{ }}4,{5.10^{ - 6}}C$
+ Hiệu điện thế giữa hai đầu tụ ${C_2}$ là:
${U_{BN}} = {\rm{ }}{U_2} + {\rm{ }}{U_3} = {\rm{ }}I{\rm{ }}\left( {{R_2} + {\rm{ }}{R_3}} \right){\rm{ }} = {\rm{ }}7,5V$
=> Điện tích tụ ${C_2}$ tích được: ${Q_2} = {\rm{ }}{C_2}{U_{BN}} = {\rm{ }}7,{5.2.10^{ - 6}} = {\rm{ }}{15.10^{ - 6}}C$
Cho mạch điện như hình vẽ: ${E_1} = {\rm{ }}12V$, ${E_2} = {\rm{ }}9V$, ${E_3} = {\rm{ }}3V$, ${r_1} = {\rm{ }}{r_2} = {\rm{ }}{r_3} = 1\Omega $ . Các điện trở ${R_1} = {R_2} = {R_3} = 2\Omega $. Hiệu điện thế ${U_{AB}}$ có giá trị:
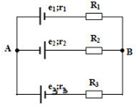
Giả sử chiều dòng điện như hình vẽ:
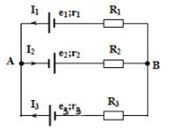
Coi $AB$ là hai cực của nguồn tương đương với $A$ - Cực dương, mạch ngoài coi như có điện trở vô cùng lớn.
\(\dfrac{1}{{{r_b}}} = \dfrac{1}{{{r_1} + {R_1}}} + \dfrac{1}{{{r_2} + {R_2}}} + \dfrac{1}{{{r_3} + {R_3}}} = \dfrac{3}{{{r_1} + {R_1}}} \to {r_b} = 1\Omega \)
\({E_b} = \dfrac{{\dfrac{{{E_1}}}{{{r_1} + {R_1}}} - \dfrac{{{E_2}}}{{{r_2} + {R_2}}} + \dfrac{{{E_3}}}{{{r_3} + {R_3}}}}}{{\dfrac{1}{{{r_b}}}}} = 2\left( V \right) = {U_{AB}}\)
Cho mạch điện như hình vẽ:
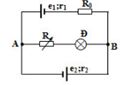
${e_1} = {\rm{ }}6V,{\rm{ }}{e_2} = {\rm{ }}18V$ , ${r_1} = {\rm{ }}{r_2} = {\rm{ }}2\Omega $; ${R_0} = {\rm{ }}4\Omega $. Đèn ghi $6V{\rm{ }} - {\rm{ }}6W$ . $R$ là biến trở.
Khi $R = 6\Omega $ đèn sáng thế nào?
Khi $R{\rm{ }} = {\rm{ }}6\Omega $
Ta xét nguồn điện tương đương gồm hai nhánh chứa hai nguồn ${e_1}$ và ${e_2}$.
Giả sử cực dương của nguồn tương đương ở A. Biến trở R và đèn là mạch ngoài.
\(\dfrac{1}{{{r_b}}} = \dfrac{1}{{{r_1} + {R_0}}} + \dfrac{1}{{{r_2}}} \to {r_b} = 1,5\Omega \)
\({e_b} = \dfrac{{\dfrac{{{e_1}}}{{{r_1} + {R_0}}} - \dfrac{{{e_2}}}{{{r_2}}}}}{{\dfrac{1}{{{r_b}}}}} = - 12V < 0\)
=> Cực dương của nguồn tương đương ở B.
Ta có điện trở của đèn: \({R_D} = \dfrac{{{U^2}}}{P} = \dfrac{{{6^2}}}{6} = 6\Omega \)
Cường độ dòng điện định mức của đèn: \({I_{dm}} = \dfrac{P}{U} = \dfrac{6}{6} = 1A\)
\({I_d} = I = \dfrac{{{e_b}}}{{R + {R_d} + {r_b}}} = \dfrac{8}{9} < {I_{dm}}\)
=> Đèn sáng yếu
Cho mạch điện như hình vẽ:
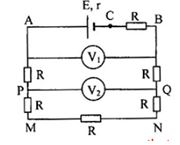
$E = 24V, r = 0$. Các vôn kế giống nhau. Số chỉ các vôn kế $V_2$ có giá trị là:
- Giả sử $R_V$ vô cùng lớn: \({R_V} = \infty \)
Số chỉ trên $V_1$ là: \({U_1} = 5R\dfrac{E}{{6R}} = \dfrac{5}{6}E = \dfrac{5}{6}.24 = 20V\)
Điều này trái với giả thiết => điều giả sử là sai hay $R_V$ hữu hạn.
- Ta có: $U_{AC} = 24V$ => $U_{BC} = 12V$
\( \to {R_{CMNB}} = R \leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R\)
Với \({R_{PQ}} = \dfrac{{3R.{R_V}}}{{3R + {R_V}}} \to {R_V} = 1,5R\)
Số chỉ trên $V_2$ : \({U_2} = \dfrac{{{U_{BC}}}}{{3R}}R = 4V\)
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({{R}_{0}}=2\text{0,3 }\!\!\Omega\!\!\text{ }\). Giá trị của r được xác định bởi thí nghiệm này là
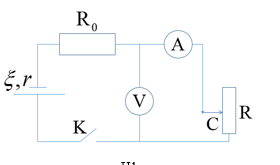 H1
H1
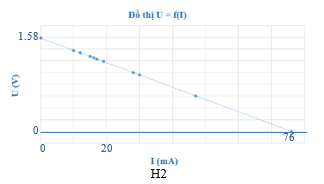
Từ đồ thị ta suy ra: \(1,58=\xi \) và \(0=1,58-({{\text{R}}_{\text{0}}}\text{+r)}\text{.0,076}\)
\(\Rightarrow {{R}_{0}}+r=20,\text{79 ( }\!\!\Omega\!\!\text{ })\Rightarrow r=0\text{,49 ( }\!\!\Omega\!\!\text{ )}\)
Sơ đồ một máy đo vạn năng được mô tả bằng hình vẽ với công tắc OB xoay được quanh trục O, có các điểm tiếp xúc 1, 2, 3, 4; các chốt M, N để nối với mạch phải đo. Để đo cường độ dòng điện, hiệu điện thế, điện trở ta phải xoay công tắc OB đến các vị trí tương ứng là:

- Khi MN là dòng điện thì để \({I_G} = {I_{MN}}\) mạch phải có điện trở rất nhỏ nên phải xoay OB đến điểm 1.
- Khi MN là hiệu điện thế thì để \({U_G} = {U_{MN}}\) mạch phải có điện trở R rất lớn để không có dòng điện chạy qua nên phải xoay OB đến điểm 2 hoặc điểm 3.
- Khi MN là điện trở thì để \({R_G} = {R_{MN}}\) ta phải xoay OB đến điểm 4vì khi đó: \({I_G} = \dfrac{E}{{{R_4} + {R_{MN}}}} \Rightarrow {R_{MN}} = \dfrac{E}{{{I_G}}} - {R_4}\), tức là với mỗi giá trị \({I_G}\) sẽ có số chỉ \({R_{MN}}\) tương ứng trên G.
Vậy thứ tự đúng là: 1 – 2 – 4

