Câu hỏi:
2 năm trước
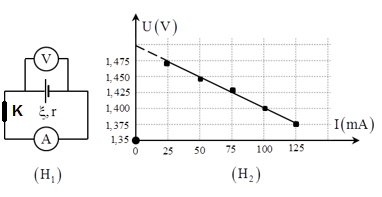
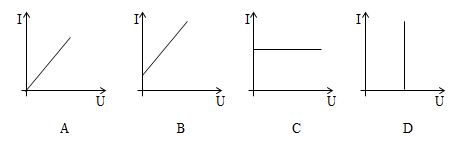
Cho mạch điện như hình vẽ:
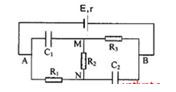
$E{\rm{ }} = {\rm{ }}12V$ , $r{\rm{ }} = {\rm{ }}2\Omega $ , ${R_1} = {\rm{ }}1\Omega $, ${R_2} = {\rm{ }}2\Omega $ , ${R_3} = {\rm{ }}3\Omega $ , ${C_1} = {\rm{ }}1\mu F$,${C_2} = {\rm{ }}2\mu F$.
Điện tích trên từng tụ điện là?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: Dòng điện một chiều không qua tụ nên mạch điện được vẽ lại như hình:
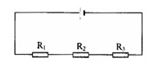
Tổng trở mạch ngoài: ${R_{ng}} = {\rm{ }}{R_1} + {\rm{ }}{R_2} + {\rm{ }}{R_3} = {\rm{ }}6\Omega $
Dòng điện qua mạch chính: \(I = \dfrac{E}{{{R_{ng}} + r}} = 1,5A\)
+ Hiệu điện thế giữa hai đầu tụ ${C_1}$là:
${U_{MA}} = {\rm{ }}{U_2} + {\rm{ }}{U_1} = {\rm{ }}I{\rm{ }}\left( {{R_2} + {\rm{ }}{R_1}} \right){\rm{ }} = {\rm{ }}4,5V$
=> Điện tích tụ ${C_1}$ tích được: ${Q_1} = {\rm{ }}{C_1}{U_{MA}} = 4,{5.10^{ - 6}} = {\rm{ }}4,{5.10^{ - 6}}C$
+ Hiệu điện thế giữa hai đầu tụ ${C_2}$ là:
${U_{BN}} = {\rm{ }}{U_2} + {\rm{ }}{U_3} = {\rm{ }}I{\rm{ }}\left( {{R_2} + {\rm{ }}{R_3}} \right){\rm{ }} = {\rm{ }}7,5V$
=> Điện tích tụ ${C_2}$ tích được: ${Q_2} = {\rm{ }}{C_2}{U_{BN}} = {\rm{ }}7,{5.2.10^{ - 6}} = {\rm{ }}{15.10^{ - 6}}C$
Hướng dẫn giải:
+ Vẽ lại mạch điện
+ Áp dụng biểu thức định luật Ôm: \(I = \dfrac{E}{{{R_N} + r}}\)
+ Áp dụng biểu thức: $Q = CU$
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
