Câu hỏi:
2 năm trước
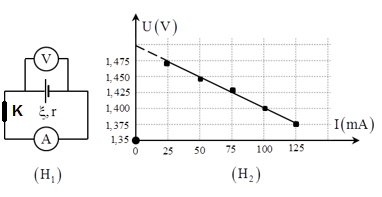
Cho mạch điện như hình vẽ:
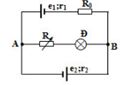
${e_1} = {\rm{ }}6V,{\rm{ }}{e_2} = {\rm{ }}18V$ , ${r_1} = {\rm{ }}{r_2} = {\rm{ }}2\Omega $; ${R_0} = {\rm{ }}4\Omega $. Đèn ghi $6V{\rm{ }} - {\rm{ }}6W$ . $R$ là biến trở.
Khi $R = 6\Omega $ đèn sáng thế nào?
Trả lời bởi giáo viên
Đáp án đúng: c
Khi $R{\rm{ }} = {\rm{ }}6\Omega $
Ta xét nguồn điện tương đương gồm hai nhánh chứa hai nguồn ${e_1}$ và ${e_2}$.
Giả sử cực dương của nguồn tương đương ở A. Biến trở R và đèn là mạch ngoài.
\(\dfrac{1}{{{r_b}}} = \dfrac{1}{{{r_1} + {R_0}}} + \dfrac{1}{{{r_2}}} \to {r_b} = 1,5\Omega \)
\({e_b} = \dfrac{{\dfrac{{{e_1}}}{{{r_1} + {R_0}}} - \dfrac{{{e_2}}}{{{r_2}}}}}{{\dfrac{1}{{{r_b}}}}} = - 12V < 0\)
=> Cực dương của nguồn tương đương ở B.
Ta có điện trở của đèn: \({R_D} = \dfrac{{{U^2}}}{P} = \dfrac{{{6^2}}}{6} = 6\Omega \)
Cường độ dòng điện định mức của đèn: \({I_{dm}} = \dfrac{P}{U} = \dfrac{6}{6} = 1A\)
\({I_d} = I = \dfrac{{{e_b}}}{{R + {R_d} + {r_b}}} = \dfrac{8}{9} < {I_{dm}}\)
=> Đèn sáng yếu
Hướng dẫn giải:
+ Áp dụng định luật Ôm cho đoạn mạch
+ Áp dụng biểu thức: \(P = UI = \dfrac{{{U^2}}}{R}\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
