Ta nên sửa tật cận thị theo cách nào thì có lợi hơn? vì sao?
Ta nhận thấy,
+ Khi đeo kính \({L_1}\) phạm vi nhìn từ \(33,3cm\) đến vô cùng
+ Khi đeo kính \({L_2}\) phạm vi nhìn từ \(25cm\) đến \(100cm\)
=> Đeo kính \({L_1}\) lợi hơn vì nó có khoảng nhìn rõ rộng hơn
Tìm khoảng cách cực cận khi đeo kính \({L_1}\) và khoảng cực viễn khi đeo kính \({L_2}\)?
- Khoảng cực cận khi đeo kính \({L_1}\)
+ Vật chỉ có thể đặt gần mắt nhất ở vị trí cho ảnh ảo ở điểm cực cận của mắt.
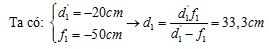
Vậy điểm gần nhất khi đeo kính \({L_1}\) còn nhìn rõ vật cách mắt là 33,3cm
- Khoảng cực cận khi đeo kính \({L_2}\)
+ Vật chỉ có thể đặt xa mắt nhất ở vị trí cho ảnh ảo ở điểm cực viễn của mắt:
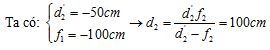
Vậy điểm xa nhất khi đeo kính \({L_2}\) còn nhìn rõ vật cách mắt là 100cm
Số kính của \({L_1};{L_2}\)là:
- Khi đeo kính \({L_1}\):
+ Qua \({L_1}\) vật ở vô cực cho ảnh ảo ở điểm cực viễn của mắt cận.
Ta có: \(\left\{ \begin{array}{l}d = \infty \\d' = - 50cm\end{array} \right. \to \frac{1}{{{f_1}}} = \frac{1}{\infty } + \frac{1}{{ - 50}} \to {f_1} = - 50cm = - 0,5m\)
+ Độ tụ: \({D_1} = \frac{1}{{{f_1}}} = - 2{\rm{d}}p\)
- Khi đeo kính \({L_2}\) :
+ Vật ở cách mắt 25cm cho ảnh ảo ở điểm cực cận của mắt.
Ta có: \(\left\{ \begin{array}{l}d = 25cm\\d' = - 20cm\end{array} \right. \to \frac{1}{{{f_2}}} = \frac{1}{{25}} + \frac{1}{{ - 20}} \to {f_2} = - 100cm = - 1m\)
+ Độ tụ: \(D = \frac{1}{f} = - 1{\rm{d}}p\)
Số kính của \({L_1};{L_2}\)là:
- Khi đeo kính \({L_1}\):
+ Qua \({L_1}\) vật ở vô cực cho ảnh ảo ở điểm cực viễn của mắt cận.
Ta có: \(\left\{ \begin{array}{l}d = \infty \\d' = - 50cm\end{array} \right. \to \frac{1}{{{f_1}}} = \frac{1}{\infty } + \frac{1}{{ - 50}} \to {f_1} = - 50cm = - 0,5m\)
+ Độ tụ: \({D_1} = \frac{1}{{{f_1}}} = - 2{\rm{d}}p\)
- Khi đeo kính \({L_2}\) :
+ Vật ở cách mắt 25cm cho ảnh ảo ở điểm cực cận của mắt.
Ta có: \(\left\{ \begin{array}{l}d = 25cm\\d' = - 20cm\end{array} \right. \to \frac{1}{{{f_2}}} = \frac{1}{{25}} + \frac{1}{{ - 20}} \to {f_2} = - 100cm = - 1m\)
+ Độ tụ: \(D = \frac{1}{f} = - 1{\rm{d}}p\)
Đặt kính \({L_1}\) cách mắt một người \(5cm\) rồi di chuyển một vật trước kính thì thấy rằng mắt nhìn rõ vật cách mắt 75mm đến 95mm. Xác định khoảng cực cận và khoảng cực viễn của mắt?
Ta có:
+ Khi vật cách mắt \(75mm = 7,5cm\) thì cách kính \({d_1} = 7,5 - 5 = 2,5cm\)
+ Khi vật ở gần thì qua kính cho ảnh ảo ở điểm cực cận của mắt, nên ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{ - \left( {O{C_C} - 5} \right)}}\\ \leftrightarrow \frac{1}{5} = \frac{1}{{2,5}} - \frac{1}{{\left( {O{C_C} - 5} \right)}}\\ \to O{C_C} = 10cm\end{array}\)
+ Khi vật ở xa thì qua kính cho ảnh ảo ở điểm cực viễn của mắt, nên ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{ - \left( {O{C_V} - 5} \right)}}\\ \leftrightarrow \frac{1}{5} = \frac{1}{{4,5}} - \frac{1}{{\left( {O{C_V} - 5} \right)}}\\ \to O{C_V} = 50cm\end{array}\)
Tiêu cự của thấu kính là:
+ Vì vật thật cho ảnh thật nên \(k < 0 \leftrightarrow - \frac{1}{2} = - \frac{{d'}}{d} \to d' = \frac{d}{2} = 7,5cm\)
+ Tiêu cự của thấu kính \(\left( {{L_1}} \right)\): \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to f = \frac{{{\rm{dd}}'}}{{d + d'}} = \frac{{15.7,5}}{{15 + 7,5}} = 5cm\)
Tiêu cự của thấu kính là:
+ Vì vật thật cho ảnh thật nên \(k < 0 \leftrightarrow - \frac{1}{2} = - \frac{{d'}}{d} \to d' = \frac{d}{2} = 7,5cm\)
+ Tiêu cự của thấu kính \(\left( {{L_1}} \right)\): \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to f = \frac{{{\rm{dd}}'}}{{d + d'}} = \frac{{15.7,5}}{{15 + 7,5}} = 5cm\)
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
Để sửa tật của mắt người bị cận thì người đó phải đeo sát mắt một kính có tiêu cự là: \(f = - O{C_V}\)
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
Để sửa tật của mắt người bị cận thì người đó phải đeo sát mắt một kính có tiêu cự là: \(f = - O{C_V}\)
Một người cận thị phải đeo sát mắt kính cận số 0,5. Nếu xem ti vi mà không muốn đeo kính thì người đó phải cách màn hình xa nhất một đoạn
Ta có:
+ Kính cận số 0,5 có \(D = - 0,5dp \to f = - 2m\)
+ Mặt khác: \(f = - O{C_V} \to O{C_V} = 2m\)
Nếu xem ti vi mà không muốn đeo kính thì người đó phải cách màn hình xa nhất một đoạn 2m
Một người cận thị về già, khi đọc sách cách mắt gần nhất 25cm phải đeo sát mắt kính số 2. Điểm cực cận của người đó nằm trên trục của mắt và cách mắt
+ Kính cận số 2 có \(D = - 2dp \to f = - 0,5m\)
+ Quan sát vật cách mắt 25cm qua kính => OCc= -d’=-df/(d+f)=50cm
Một người viễn thị có điểm cực cận cách mắt 50cm. Khi đeo sát mắt một kính có độ tụ +1dp, người này sẽ nhìn rõ được những vật gần nhất cách mắt
+ Ta có: \(D = 1dp \to f = 1m\)
+ Quan sát vật cách mắt 50cm qua kính:
\( \to O{C_C} = - d' \to d = \frac{{d'f}}{{d' - f}} = 33.3cm\)
Một người viễn thị có điểm cực cận cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( đeo sát mắt) có độ tụ là:
+ Theo công thức thấu kính: \(D = \dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{{0,25}} + \dfrac{1}{{ - 0,4}} = 1,5dp\)
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt ) chữa tật của mắt để khi nhìn vật ở vô cực mà mắt không điều tiết, người này nhìn rõ được các vật đặt gần nhất cách mắt
- Người đó sửa tật khi đeo kính có f= -OCv= -50cm
- Quan sát ở cực cận:
\(d' = - O{C_c} = - 12,5cm \Rightarrow d = \dfrac{{d'f}}{{d' - f}} = 16,7cm\)
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt) có độ tụ -1dp. Khoảng nhìn rõ của người này khi đeo kính là
Người đó đeo kính có f= -1m
=> Quan sát ở cực cận: \(d' = - O{C_C} = - 12,5cm \to {d_C} = \frac{{d'f}}{{d' - f}} = 14,3cm\)
=> Quan sát ở cực viễn : \(d' = - O{C_v} = - 50cm \to {d_V} = \frac{{d'f}}{{d' - f}} = 100cm\)
=> Khoảng nhìn rõ của người này khi đeo kính là \(14,3cm - 100cm\)
Một người viễn thị nhìn rõ được vật đặt cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( kính cách mắt 1cm) có độ tụ là
+ Người đó sửa tật khi đeo kính có:\(d' = - OC_{C} + l = - 39cm\)
+ Quan sát ở cực cận: \(d = 25 - 1 = 24cm\)
\(D = \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{0,24}} + \frac{1}{{ - 0,39}} = 1,6dp\)
Mắt một người cận thị có khoảng nhìn rõ từ 12cm đến 51cm. Người đó sửa tật bằng cách đeo kính phân kì cách mắt 1cm. Biết năng suất phân li của mắt là 1’. Khoảng cách nhỏ nhất giữa hai điểm trên vật mà mắt còn có thể phân biệt được là
+ Người đó sửa tật khi đeo kính có \(f = - O{C_C} + l = - 50cm\)
+ Khoảng cách nhỏ nhất giữa hai điểm trên vật khi quan át ở cực cận có ảnh cách mắt \(l = 12cm\)
=> Khoảng cách nhỏ nhất hai điểm trên ảnh là:\(A'B' = l\alpha \)
Trong đó: \(\alpha = 1' = \dfrac{1}{{60}}\) độ = \(\dfrac{1}{{60}}.\dfrac{\pi }{{180}}\) (rad)
Suy ra: \(A'B' = l\alpha = 12.\dfrac{1}{{60}}\dfrac{\pi }{{180}} = 3,{49.10^{ - 3}}cm = 0,0349mm\)
+ Ảnh nằm cách kính một đoạn \(d' = - 11cm\)
Theo công thức thấu kính:
\(\begin{array}{l}k = \dfrac{{A'B'}}{{AB}} = \dfrac{{ - d' - f}}{f} = \dfrac{{ - \left( { - 11 + 50} \right)}}{{ - 50}} = 0,78\\ \to AB = \dfrac{{A'B'}}{{0,78}} = \dfrac{{0,0349}}{{0,78}} = 0,0447mm\end{array}\)
Mắt một người có điểm cực viễn cách mắt 50cm và độ biến thiên độ tụ từ trạng thái mắt không điều tiết đến trạng thái mắt điều tiết tối đa là 8dp. Hỏi điểm cực cận của mắt người này cách mắt bao nhiêu?
Ta có: biến thiên độ tụ khi chuyển từ trạng thái khống điều tiết sang điều tiết tối đa: \(\begin{array}{l}\Delta D = \frac{1}{{O{C_C}}} - \frac{1}{{O{C_V}}} \leftrightarrow 8 = \frac{1}{{O{C_C}}} - \frac{1}{{0,5}}\\ \to O{C_C} = 0,1m = 10cm\end{array}\)
Trên một tờ giấy vẽ hai vạch cách nhau 1mm. Đưa tờ giấy xa mắt dần cho đến khi thấy hai vạch đó gần như nằm trên một đường thẳng. Xác định gần đúng khoảng cách từ mắt đến tờ giấy. Biết năng suất phân li của mắt người này là \({\alpha _{\min }} = {3.10^{ - 4}}ra{\rm{d}}\).
Ta có:
+ Khoảng cách giữa hai vạch xem như vật AB có chiều cao 1mm
+ Góc trông vật của mắt: \(\tan \alpha = \frac{{AB}}{l}\) (với \(l\) là khoảng cách từ mắt đến tờ giấy)
+ Khi mắt thấy hai vạch đó như nằm trên một đường thẳng thì \({\alpha _{\min }}\), khi đó
\(\begin{array}{l}\tan {a_{\min }} = \frac{{AB}}{{{l_{{\rm{max}}}}}}\\ \to {l_{{\rm{max}}}} = \frac{{AB}}{{\tan {\alpha _{\min }}}} \approx \frac{{AB}}{{{\alpha _{\min }}}} = \frac{{{{10}^{ - 3}}}}{{{{3.10}^{ - 4}}}} = 3,33m\end{array}\)
Một mắt bình thường có võng mạc cách thủy tinh thể một đoạn 15mm. Hãy xác định độ tụ của thủy tinh thể khi nhìn vật AB trong các trường hợp
Vật AB ở vô cực?
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ Khi nhìn vật ở vô cực \(\left( {d = \infty } \right)\), ảnh hiện trên võng mạc.
+ Tiêu cự của thủy tinh thế là:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{OV}}\\ \to f = OV = 15mm\end{array}\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{{{15.10}^{ - 3}}}} = 66,67{\rm{d}}p\)

