Một bóng đèn có ghi (6V – 9 W) được mắc vào một nguồn điện có suất điện động \(\xi = 9{\rm{ (V)}}\). Để đèn sáng bình thường, điện trở trong r của nguồn điện phải có độ lớn bằng
Điện trở của bóng đèn là:
\(R = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}} = \dfrac{{{6^2}}}{9} = 4\Omega \)
Để đèn sáng bình thường thì hiệu điện thế giữa hai đầu bóng đèn bằng hiệu điện thế định mức của bóng đèn.
Hiệu điện thế giữa hai đầu bóng đèn là
\({{U}_{}}=I.R\Rightarrow I=\dfrac{{{U}_{}}}{R}=\dfrac{6}{4}1,5A\)
Áp dụng định luật Ôm với toàn mạch :
\(I = \dfrac{\xi }{{R + r}} \Leftrightarrow 1,5 = \dfrac{9}{{4 + r}} \Rightarrow r = 2\Omega \)
Một nguồn điện có suất điện động E = 12V và điện trở trong \(2\Omega \). Nối điện trở R vào hai cực của nguồn điện thành mạch kín thì thì công suất tiêu thụ điện trên điện trở R bằng 16W. Biết \(R > 2\Omega \), giá trị của điện trở R bằng
Cường độ dòng điện trong mạch: \(I = \frac{E}{{R + r}} = \frac{{12}}{{R + 2}}\)
Công suất tiêu thụ trên R: \({P_R} = {I^2}R = 16{\rm{W}}\)
\( \Leftrightarrow \frac{{{{12}^2}}}{{{{\left( {R + 2} \right)}^2}}}R = 16 \Rightarrow \left[ \begin{array}{l}R = 4\Omega \\R = 1\Omega \,\,\,\,\left( {loai} \right)\end{array} \right.\)
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở?
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở là: \(I = \frac{U}{R}\)
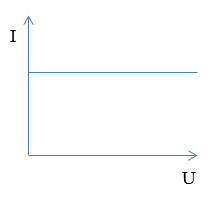
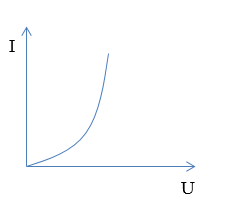
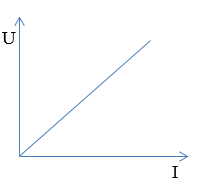
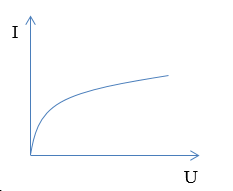
Đồ thị nào sau đây diễn tả đúng mối liên hệ giữa hiệu điện thế $(U)$ và cường độ dòng điện $(I)$ trong đoạn mạch chỉ có điện trở?
Ta có: Biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R} \to U = IR\)
=> Đồ thị có dạng của hàm số y = ax
Cho đoạn mạch gồm R1 mắc nối tiếp với R2, biểu thức nào sau đây là sai ?
A, B, D - đúng
C - sai vì : khi R1 mắc nối tiếp với R2 thì I = I1 = I2
Cho đoạn mạch gồm R1 mắc song song với R2, biểu thức nào sau đây là đúng?
Khi R1 mắc song song với R2 ta có:
\(\begin{array}{l}\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} \to R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\U = {U_1} = {U_2}\\I = {I_1} + {I_2}\end{array}\)
Cho mạch điện như hình vẽ:
Trong đó: R1 = R2 = 4$\Omega $, R3 = 6$\Omega $, R4 = 3$\Omega $, R5 = 10$\Omega $
Tính điện trở tương đương của đoạn mạch AB?
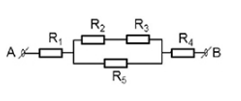
Giả sử chiều dòng điện từ A đến B.
Ta có: I qua R1 không bị phân nhánh => R1 mắc nối tiếp
Tại M, I bị phân nhánh, I’ qua R2, R3 không phân nhánh => (R2 nt R3 ) // R5
I qua R4 không phân nhánh
Vậy: đoạn mạch gồm: R1 nt [(R2 nt R3) // R5 ] nt R4
\({R_{23}} = {R_2} + {R_3} = 4 + 6 = 10\Omega \)
\(\frac{1}{{{R_{235}}}} = \frac{1}{{{R_{23}}}} + \frac{1}{{{R_5}}} \to {R_{235}} = \frac{{{R_{23}}.{R_5}}}{{{R_{23}} + {R_5}}} = \frac{{10.10}}{{10 + 10}} = 5\Omega \)
Tổng trở của toàn mạch:
\(R = {R_1} + {R_{235}} + {R_4} = 4 + 5 + 3 = 12\Omega \)
Cho mạch điện như hình vẽ.
R1 = 2,4$\Omega $, R2 = 14$\Omega $, R3 = 4$\Omega $, R4 = R5 = 6$\Omega $, I3 = 2A.
Hiệu điện thế giữa hai đầu đoạn mạch UAB là?
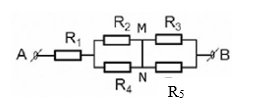
Ta nhận thấy giữa hai điểm M, N không có điện trở => ta có thể chập lại thành một điểm khi đó mạch trở thành:
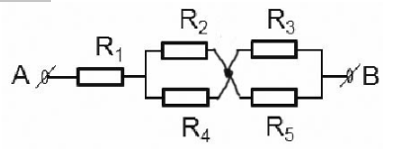
=> Đoạn mạch gồm: R1 nt (R2 // R4) nt (R3 // R5)
\(\frac{1}{{{R_{24}}}} = \frac{1}{{{R_2}}} + \frac{1}{{{R_4}}} \to {R_{24}} = \frac{{{R_2}{R_4}}}{{{R_2} + {R_4}}} = \frac{{14.6}}{{14 + 6}} = 4,2\Omega \)
\(\frac{1}{{{R_{35}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_5}}} \to {R_{35}} = \frac{{{R_3}{R_5}}}{{{R_3} + {R_5}}} = \frac{{4.6}}{{4 + 6}} = 2,4\Omega \)
\(R = {R_1} + {R_{24}} + {R_{35}} = 2,4 + 4,2 + 2,4 = 9\Omega \)
Ta có: U3 = U5 = U35 = I3.R3 = 2.4 = 8V
\( \to {I_5} = \frac{{{U_5}}}{{{R_5}}} = \frac{8}{6} = \frac{4}{3}A \to {I_{35}} = {I_3} + {I_5} = 2 + \frac{4}{3} = \frac{{10}}{3}A\)
\(I = {I_1} = {I_{24}} = {I_{35}} = \frac{{10}}{3}A \to {U_{AB}} = IR = \frac{{10}}{3}.9 = 30V\)
Cho mạch điện như hình vẽ:
Trong đó R1 = R3 = R5 = 3$\Omega $, R2 = 8$\Omega $, R4 = 6$\Omega $, U = 12V.
Cường độ dòng điện chạy qua đoạn mạch AB là?
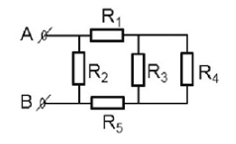
Đặt tên các điểm như hình
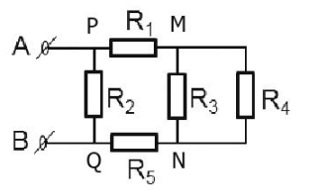
Vẽ lại đoạn mạch, ta được:
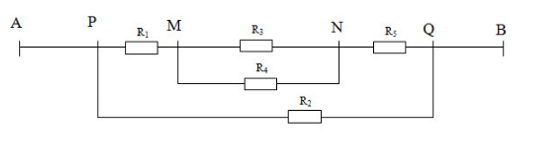
Đoạn mạch gồm: R2 // [ R1 nt (R3 // R4) nt R5)
\(\frac{1}{{{R_{34}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_4}}} \to {R_{34}} = \frac{{{R_3}{R_4}}}{{{R_3} + {R_4}}} = \frac{{3.6}}{{3 + 6}} = 2\Omega \)
\({R_{1345}} = {R_1} + {R_{34}} + {R_5} = 3 + 2 + 3 = 8\Omega \)
Tổng trở của mạch:
\(\frac{1}{R} = \frac{1}{{{R_2}}} + \frac{1}{{{R_{1345}}}} \to R = \frac{{{R_2}{R_{1345}}}}{{{R_2} + {R_{1345}}}} = \frac{{8.8}}{{8 + 8}} = 4\Omega \)
Cường độ dòng điện trong mạch:
\(I = \frac{U}{R} = \frac{{12}}{4} = 3A\)
Cho mạch điện như hình vẽ:
Trong đó R1 = 8$\Omega $, R3 = 10$\Omega $, R2 = R4 = R5 = 20$\Omega $, I3 = 2A. Tổng trở của mạch và hiệu điện thế qua R2 là?
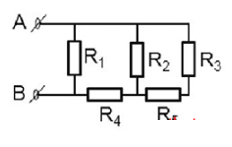
Vẽ lại mạch điện ta được:
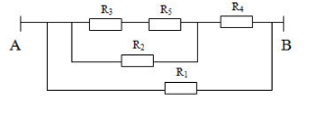
Đoạn mạch gồm: R1 // ( R4 nt (R2 // (R3 nt R5)))
R35 = R3+ R5 = 10 + 20 = 30$\Omega $
\(\frac{1}{{{R_{235}}}} = \frac{1}{{{R_2}}} + \frac{1}{{{R_{35}}}} \to {R_{235}} = \frac{{{R_2}.{R_{35}}}}{{{R_2} + {R_{35}}}} = \frac{{20.30}}{{20 + 30}} = 12\Omega \)
R4235 = R4 + R235 = 20 + 12 = 32$\Omega $
\(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_{4235}}}} \to R = \frac{{{R_1}.{R_{4235}}}}{{{R_1} + {R_{4235}}}} = \frac{{8.32}}{{8 + 32}} = 6,4\Omega \)
Ta có: I3 = I5 = I35 = 2A
U2 = U235 = U35 = I35.R35 = 2.30 = 60V
Tính điện trở tương đương của đoạn mạch sau:
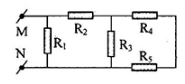
Biết $R_1 = 1\Omega $, $R_2 = 2,4\Omega $, $R_3 = 2\Omega $, $R_4 = 5\Omega $, $R_5 = 3\Omega $
Ta có, đoạn mạch gồm: \({R_1}\backslash \backslash ({R_2}nt({R_3}\backslash \backslash ({R_4}nt{R_5})))\)
+ \(\left( {{R_4}nt{R_5}} \right)\), ta suy ra: ${R_{45}} = {\rm{ }}{R_4} + {\rm{ }}{R_5} = {\rm{ }}5{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}8\Omega $
+\({R_3}\backslash \backslash {R_{45}}\), ta suy ra:
\(\dfrac{1}{{{R_{345}}}} = \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_{45}}}} \to {R_{345}} = \dfrac{{{R_3}{R_{45}}}}{{{R_3} + {R_{45}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
+ \({R_2}nt{R_{345}}\) , ta suy ra:
${R_{2345}} = {\rm{ }}{R_2} + {\rm{ }}{R_{345}} = {\rm{ }}2,4{\rm{ }} + {\rm{ }}1,6{\rm{ }} = {\rm{ }}4\Omega $
+ \({R_1}\backslash \backslash {R_{2345}}\), ta suy ra:
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{2345}}}} \to R = \dfrac{{{R_1}{R_{2345}}}}{{{R_1} + {R_{2345}}}} = \dfrac{{1.4}}{{1 + 4}} = 0,8\Omega $
Cho mạch điện như hình vẽ:
R1 = R2 = R3 = 6$\Omega $, R4 = 2$\Omega $. Tính điện trở tương đương của mạch khi ta nối M và B bằng một ampe kế có điện trở rất nhỏ?
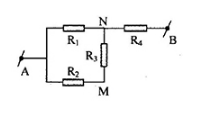
Vì ampe kế có điện trở rất nhỏ nên M và B cùng điện thế
=> chập M và B mạch điện được vẽ lại như hình
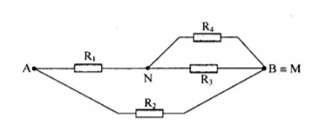
Ta có: R2 // ((R1 nt (R3//R4))
\(\frac{1}{{{R_{34}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_4}}} \to {R_{34}} = \frac{{{R_3}{R_4}}}{{{R_3} + {R_4}}} = \frac{{6.2}}{{6 + 2}} = 1,5\Omega \)
R134 = R1 + R34 = 6 + 1,5 = 7,5$\Omega $
Điện trở tương đương của toàn mạch:
\(\frac{1}{R} = \frac{1}{{{R_2}}} + \frac{1}{{{R_{134}}}} \to R = \frac{{{R_2}{R_{134}}}}{{{R_2} + {R_{134}}}} = \frac{{6.7,5}}{{6 + 7,5}} = \frac{{10}}{3}\Omega \)
Cho mạch điện như hình vẽ:
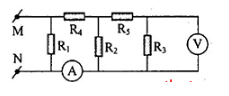
\(U_{MN}= 4V\), \(R_1=R_2=2\Omega\), \(R_3=R_4=R_5=1\Omega\), RA = 0, RV = ∞. Số chỉ của ampe kế và vôn kế là?
Vẽ lại mạch điện ta được:
Ta có: R1 // ( R4 nt (R2 // (R3 nt R5)))
R35 = R3 + R5 = 1+1 = 2$\Omega $
\(\dfrac{1}{{{R_{235}}}} = \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_{35}}}} \\\to {R_{235}} = \dfrac{{{R_2}{R_{35}}}}{{{R_2} + {R_{35}}}} = \dfrac{{2.2}}{{2 + 2}} = 1\Omega \)
R4235 = R4 + R235 = 1 + 1 = 2$\Omega $
Tổng trở của mạch:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{4235}}}} \\\to R = \dfrac{{{R_1}{R_{4235}}}}{{{R_1} + {R_{4235}}}} = \dfrac{{2.2}}{{2 + 2}} = 1\Omega \)
Ta có, số chỉ của ampe kế chính là cường độ dòng \(I_1\)
Mặt khác, ta có: UMN = U1 = U4235
\({I_1} = \dfrac{{{U_{MN}}}}{{{R_{1}}}} = \dfrac{4}{2} = 2{\rm{A}}\)
Số chỉ của vôn kế là U3 = I3R3
Ta có: U35 = UMN - U4 = 4 - 2.1= 2V
\( \to {I_{35}} = \dfrac{{{U_{35}}}}{{{R_{35}}}} = \dfrac{2}{2} = 1{\rm{A}} \\\to {{\rm{U}}_3} = {I_{35}}{R_3} = 1.1 = 1V\)
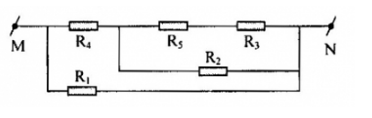
Cho mạch điện như hình vẽ
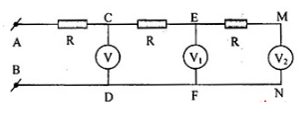
Biết 3 vôn kế giống nhau, UV = 5V, UV2 = 1V. Số chỉ của vôn kế V1 là bao nhiêu?
Giả sử các vôn kế có điện trở vô cùng lớn, khi đó mạch chỉ gồm các điện trở nối tiếp.
Ta có:
\(\left\{ \begin{array}{l}{U_{CD}} = V = I.2R\\{U_{MN}} = {V_2} = 0\end{array} \right.\)
=> Vôn kế có điện trở RV không phải rất lớn so với R.
+ Xét đoạn mạch MN:
\({I_{V2}}{R_V} = {\rm{ }}1 \to {I_{V2}} = \dfrac{1}{{{R_V}}}\)
+ Xét đoạn mạch EF:
\(\begin{array}{l}{U_{EF}} = {I_{V1}}{R_V} = {I_{V2}}R + {U_{MN}} \\= {I_{V2}}R + 1 = \dfrac{R}{{{R_V}}} + 1\\ \to {I_{V1}} = \dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}}\end{array}\)
+ Xét đoạn mạch CD:
\(\begin{array}{l}{U_{CD}} = {I_1}R + {U_{EF}} \\= {I_1}R + \dfrac{R}{{{R_V}}} + 1 = 5\\ \leftrightarrow {I_1}R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow ({I_{V1}} + {I_{V2}})R + \dfrac{R}{{{R_V}}} = 4\\ \leftrightarrow \left( {\dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}} + \dfrac{1}{{{R_V}}}} \right)R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow \dfrac{{{R^2}}}{{R_V^2}} + \dfrac{{3R}}{{{R_V}}} = 4\\ \leftrightarrow {R^2} + 3{\rm{R}}{{\rm{R}}_V} - 4{\rm{R}}_V^2 = 0\\ \to R = {R_V}\end{array}\)
Vậy
\({U_{EF}} = {\rm{ }}{I_{V1}}{R_V} = {\rm{ }}{I_{V2}}R{\rm{ }} + {\rm{ }}{U_{MN}} \\= \dfrac{R}{{{R_V}}}{\rm{ }} + {\rm{ }}1 = 2V\)
Có hai loại điện trở 5$\Omega $ và 7$\Omega $. Số điện trở mỗi loại sao cho khi ghép nối tiếp ta được điện trở tổng cộng 95$\Omega $ với số điện trở là nhỏ nhất là?
Gọi x, y lần lượt là số điện trở 5$\Omega $ và 7$\Omega $. (x, y là số nguyên không âm)
Theo đề bài, ta có:
\(5{\rm{x}} + 7y = 95 \to x = 19 - \frac{7}{5}y\)
vì \(x \ge 0 \to 19 - \frac{7}{5}y \ge 0 \to y \le 13,6{\rm{ }}(*)\)
Để x là số nguyên không âm thì y phải là bội của 5 hoặc y = 0 và thỏa mãn điều kiện (*) .
Vậy:
+ y = 0 thì x = 19
+ y = 5 thì x = 12
+ y = 10 thì x = 5
Vì tổng số điện trở nhỏ nhất => chọn x = 5 và y = 10.
Vậy cần ít nhất 5 điện trở loại 5$\Omega $ và 10 điện trở loại 7$\Omega $. tổng = 15 điện trở
Một mạch điện gồm vô hạn những nhóm cấu tạo từ 3 điện trở giống nhau r như hình vẽ. Điện trở tương đương của mạch điện là bao nhiêu? Coi rằng việc bỏ đi nhóm điện trở (1) thì cũng không làm thay đổi điện trở tương đương của toàn mạch.
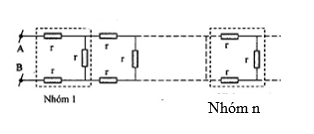
Gọi R - điện trở tương đương của toàn mạch
Vì mạch điện có nhiều nhóm giống nhau nên nếu không kể nhóm (1) thì điện trở toàn mạch xem như cũng không đổi, nghĩa là vẫn bằng R.
Ta có mạch điện tương đương như hình vẽ
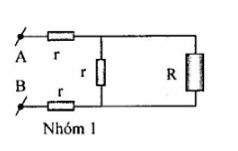
Ta có:
\(\begin{array}{l}R = 2{\rm{r + }}\dfrac{{{\mathop{\rm R}\nolimits} {\rm{r}}}}{{R + r}} \\\to {R^2} - 2{\rm{r}}R - 2{{\rm{r}}^2} = 0\\\Delta ' = {r^2} + 2{{\rm{r}}^2} = 3{{\rm{r}}^2}\\ \to \left[ \begin{array}{l}R = r + \sqrt 3 r\\R = r - \sqrt 3 r < 0(loai)\end{array} \right. \\\to R = r + \sqrt 3 r\end{array}\)
Cho mạch điện như hình vẽ: R2 = 10$\Omega $, UMN = 30V. Biết khi K1 đóng, K2 mở ampe kế chỉ 1A. Khi K1 mở, K2 đóng thì ampe kế A chỉ 2A. Số chỉ của ampe kế A khi cả 2 khóa K1 và K2 cùng đóng là?
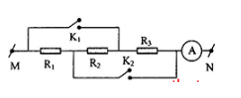
Khi K1 đóng còn K2 mở thì mạch chỉ có R3 \( \to {R_3} = \frac{{30}}{1} = 30\Omega \)
Khi K2 đóng, K1 mở thì mạch chỉ có R1 \( \to {R_1} = \frac{{30}}{2} = 15\Omega \)
Khi K1 và K2 cùng đóng thì : R1 // R2 // R3:
Điện trở tương đương của mạch:
\(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{{15}} + \frac{1}{{10}} + \frac{1}{{30}} = \frac{1}{5} \to R = 5\Omega \)
Ta có, số chỉ ampe kế chính là I mạch chính: \(I = \frac{{{U_{MN}}}}{R} = \frac{{30}}{5} = 6A\)
Cho mạch điện như hình vẽ:
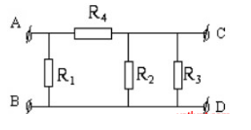
Biết R3 = R4. Nếu nối hai đầu AB vào hiệu điện thế 120V thì cường độ dòng điện qua R2 là 2A và UCD = 30V. Nếu nối hai đầu CD vào hiệu điện thế 120V thì UAB = 20V. R1 có giá trị là?
+ Trường hợp hiệu điện thế đặt vào AB
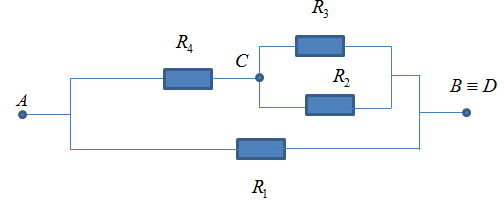
Mạch gồm: R1 // ( R4 nt (R3 // R2))
Ta có: UAC = UAB- UCD = 120 - 30 = 90V
\({R_3} = {\rm{ }}{R_4} \to {I_4} = \dfrac{{{U_{AC}}}}{{{R_4}}} = \dfrac{{90}}{{{R_4}}} = \dfrac{{90}}{{{R_3}}} = {I_2} + {I_3} = 2 + \dfrac{{30}}{{{R_3}}} \to {R_3} = {R_4} = 30\Omega \)
+ Trường hợp hiệu điện thế đặt vào CD
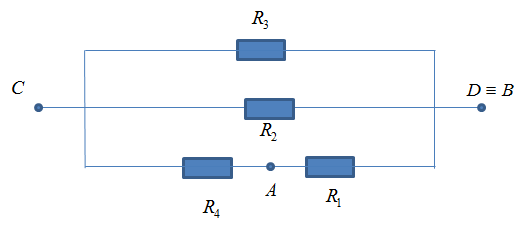
Mạch gồm R3 // ( R2 // (R1 nt R4))
=> UAC = UCD - UAB = 100V
\({I_4} = {I_1} = \dfrac{{{U_{AC}}}}{{{R_4}}} = \dfrac{{10}}{3}A\)
\({R_1} = \dfrac{{{U_{AB}}}}{{{I_1}}} = \dfrac{{20}}{{\dfrac{{10}}{3}}} = 6\Omega \)
Một nguồn điện có điện trở trong 0,1 (Ω) được mắc với điện trở 4,8 (Ω) thành mạch kín. Khi đó hiệu điện thế giữa hai cực của nguồn điện là 12 (V). Suất điện động E của nguồn điện là:
Cường độ dòng điện của mạch kín là:
\(I = \dfrac{U}{R} = \dfrac{{12}}{{4,8}} = 2,5A\)
Áp dụng định luật Ôm cho toàn mạch ta có:
\(I = \dfrac{E}{{R + r}} \Rightarrow E = I.\left( {R + r} \right) = 2,5.\left( {4,8 + 0,1} \right) = 12,25V\)
Cho mạch đện như hình vẽ. Nguồn điện có suất điện động 24V, điện trở trong r = 4 Ω, R = 3Ω, Rx là biến trở có giá trị từ 0 đến 100Ω. Tìm Rx để công suất mạch ngoài là PN = 20W.
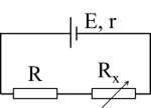
Ta có: R nt Rx => RN = R + Rx
Áp dụng định luật ôm cho toàn mạch ta có:
\(I = \dfrac{E}{{R + {R_x} + r}}\)
Công suất mạch ngoài là:
\({P_N} = {I^2}{R_N} = \dfrac{{{E^2}{R_N}}}{{{{\left( {r + R + {R_x}} \right)}^2}}}\)
\(\begin{array}{l}{P_N} = 20 \Leftrightarrow \dfrac{{{{24}^2}.\left( {3 + {R_x}} \right)}}{{{{\left( {4 + 3 + {R_x}} \right)}^2}}} = 20\\ \Leftrightarrow \left[ \begin{array}{l}{R_x} = 17\Omega \\{R_x} = - 2,2(loai)\end{array} \right.\end{array}\)
Vậy \({R_x} = 17\Omega \)