Định luật Ôm cho đoạn mạch chỉ có điện trở

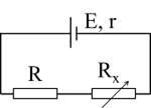
Ta có:

Công suất mạch ngoài là:

\({P_N} = {I^2}{R_N} = \frac{{{E^2}{R_N}}}{{{{\left( {r + R + {R_x}} \right)}^2}}}\)\( = \frac{{{E^2}}}{{{{\left( {\frac{r}{{R + {R_x}}} + 1} \right)}^2}}}\)

\({P_{\max }} \Leftrightarrow {\left( {\frac{r}{{R + {R_x}}} + 1} \right)_{\min }}\)

Áp dụng bất đẳng thức cô-si cho hai số dương \(\frac{r}{{R + {R_x}}}\) và 1 ta có:

\(\left( {\frac{r}{{R + {R_x}}} + 1} \right) \ge 2.\sqrt {\frac{r}{{R + {R_x}}}} \)

Dấu “=” xảy ra khi và chỉ khi \(\frac{r}{{R + {R_x}}} = 1 \Leftrightarrow \frac{4}{{3 + {R_x}}} = 1 \Leftrightarrow {R_x} = 1\Omega \)

Công suất cực đại: \({P_{\max }} = \frac{{{{24}^2}.\left( {3 + 1} \right)}}{{{{(4 + 3 + 1)}^2}}} = 36{\rm{W}}\)

Vậy \({R_x} = 1\Omega ;{P_{\max }} = 36{\rm{W}}\)

Hiệu điện thế giữa hai cực nguồn điện là:

\(U = I.R \Rightarrow I = \dfrac{U}{R} = \dfrac{{12}}{{4,8}} = 2,5\,\,\left( A \right)\)

Hiệu điện thế giữa hai cực của nguồn điện khi điện trở mạch ngoài là \({R_1};\,\,{R_2}\) là:

\(\left\{ \begin{array}{l}{U_1} = {I_1}{R_1} = 3{I_1}\\{U_2} = {I_2}{R_2} = 10,5{I_2}\end{array} \right.\)

Ta có: \({U_2} = 2{U_1} \Rightarrow 10,5{I_2} = 2.3{I_1} \Rightarrow {I_2} = \frac{4}{7}{I_1}\)

\(\begin{array}{l} \Rightarrow \dfrac{E}{{{R_2} + r}} = \dfrac{4}{7}.\dfrac{E}{{{R_1} + r}} \Rightarrow 7\left( {{R_1} + r} \right) = 4\left( {{R_2} + r} \right)\\ \Rightarrow r = \frac{{4{R_2} - 7{R_1}}}{3} = \frac{{4.10,5 - 7.3}}{3} = 7\,\,\left( \Omega  \right)\end{array}\)

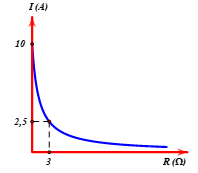
Cường độ dòng điện trong toàn mạch: \(I = \frac{E}{{R + r}}\)

Từ đồ thị, ta có:

+ Khi \(R = 0\Omega  \Rightarrow I = 10A = \frac{E}{r}\,\,\,\,\left( 1 \right)\)

+ Khi \(R = 3\Omega  \Rightarrow I = 2,5A = \frac{E}{{R + r}} = \frac{E}{{3 + r}}\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}E = 10V\\r = 1\Omega \end{array} \right.\)

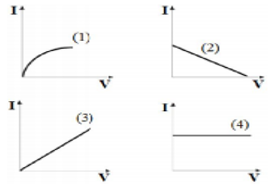
Đồ thị biểu diễn định luật Ôm cho điện trở của kim loại là đồ thị (3).