Câu hỏi:
2 năm trước
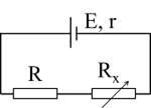
Cho mạch đện như hình vẽ. Nguồn điện có suất điện động 24V, điện trở trong r = 4 Ω, R = 3Ω, Rx là biến trở có giá trị từ 0 đến 100Ω. Tìm Rx để công suất mạch ngoài cực đại. Tính giá trị cực đại đó.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
Công suất mạch ngoài là:
\({P_N} = {I^2}{R_N} = \frac{{{E^2}{R_N}}}{{{{\left( {r + R + {R_x}} \right)}^2}}}\)\( = \frac{{{E^2}}}{{{{\left( {\frac{r}{{R + {R_x}}} + 1} \right)}^2}}}\)
\({P_{\max }} \Leftrightarrow {\left( {\frac{r}{{R + {R_x}}} + 1} \right)_{\min }}\)
Áp dụng bất đẳng thức cô-si cho hai số dương \(\frac{r}{{R + {R_x}}}\) và 1 ta có:
\(\left( {\frac{r}{{R + {R_x}}} + 1} \right) \ge 2.\sqrt {\frac{r}{{R + {R_x}}}} \)
Dấu “=” xảy ra khi và chỉ khi \(\frac{r}{{R + {R_x}}} = 1 \Leftrightarrow \frac{4}{{3 + {R_x}}} = 1 \Leftrightarrow {R_x} = 1\Omega \)
Công suất cực đại: \({P_{\max }} = \frac{{{{24}^2}.\left( {3 + 1} \right)}}{{{{(4 + 3 + 1)}^2}}} = 36{\rm{W}}\)
Vậy \({R_x} = 1\Omega ;{P_{\max }} = 36{\rm{W}}\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
