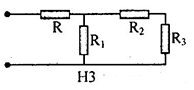
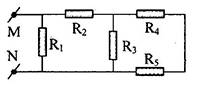
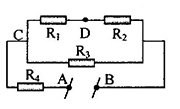
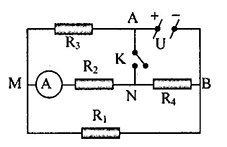
Cho mạch điện như hình vẽ
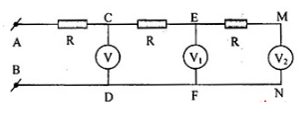
Biết 3 vôn kế giống nhau, UV = 5V, UV2 = 1V. Số chỉ của vôn kế V1 là bao nhiêu?
Trả lời bởi giáo viên
Giả sử các vôn kế có điện trở vô cùng lớn, khi đó mạch chỉ gồm các điện trở nối tiếp.
Ta có:
\(\left\{ \begin{array}{l}{U_{CD}} = V = I.2R\\{U_{MN}} = {V_2} = 0\end{array} \right.\)
=> Vôn kế có điện trở RV không phải rất lớn so với R.
+ Xét đoạn mạch MN:
\({I_{V2}}{R_V} = {\rm{ }}1 \to {I_{V2}} = \dfrac{1}{{{R_V}}}\)
+ Xét đoạn mạch EF:
\(\begin{array}{l}{U_{EF}} = {I_{V1}}{R_V} = {I_{V2}}R + {U_{MN}} \\= {I_{V2}}R + 1 = \dfrac{R}{{{R_V}}} + 1\\ \to {I_{V1}} = \dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}}\end{array}\)
+ Xét đoạn mạch CD:
\(\begin{array}{l}{U_{CD}} = {I_1}R + {U_{EF}} \\= {I_1}R + \dfrac{R}{{{R_V}}} + 1 = 5\\ \leftrightarrow {I_1}R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow ({I_{V1}} + {I_{V2}})R + \dfrac{R}{{{R_V}}} = 4\\ \leftrightarrow \left( {\dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}} + \dfrac{1}{{{R_V}}}} \right)R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow \dfrac{{{R^2}}}{{R_V^2}} + \dfrac{{3R}}{{{R_V}}} = 4\\ \leftrightarrow {R^2} + 3{\rm{R}}{{\rm{R}}_V} - 4{\rm{R}}_V^2 = 0\\ \to R = {R_V}\end{array}\)
Vậy
\({U_{EF}} = {\rm{ }}{I_{V1}}{R_V} = {\rm{ }}{I_{V2}}R{\rm{ }} + {\rm{ }}{U_{MN}} \\= \dfrac{R}{{{R_V}}}{\rm{ }} + {\rm{ }}1 = 2V\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: R = R1 + R2 + .... + Rn
+ Áp dụng biểu thức xác định điện trở trong mạch song song:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)