Câu hỏi:
2 năm trước
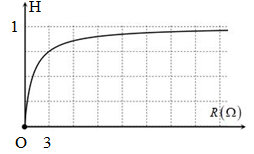
Mắc một biến trở R vào hai cực của một nguồn điện một chiều có suất điện động \(\xi = 6V\) và điện trở trong \(r\). Đồ thị biểu diễn hiệu suất H của nguồn điện theo biến trở R như hình vẽ bên. Công suất tiêu thụ cực đại trên R có giá trị bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)
Từ đồ thị ta có tại \(R = 3\Omega \) thì \(H = 0,75\)
\( \Leftrightarrow \frac{R}{{R + r}} = 0,75 \Leftrightarrow \frac{3}{{3 + r}} = 0,75 \Rightarrow r = 1\Omega \)
Công suất tiêu thụ trên R:
\({P_R} = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\)
\( \Rightarrow {P_{Rma{\rm{x}}}}\) khi \({\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)^2}_{\min }\)
Áp dụng BĐT Cosi ta có: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r = 2\)
\( \Rightarrow \sqrt R + \frac{r}{{\sqrt R }} = 2\sqrt r = 2\) khi \(\sqrt R = \frac{r}{{\sqrt R }}\)hay \(R = r\)
\( \Rightarrow {P_{R\max }} = \frac{{{E^2}}}{{4{\rm{R}}}} = \frac{{{E^2}}}{{4{\rm{r}}}} = \frac{{{6^2}}}{4} = 9W\)
Hướng dẫn giải:
+ Đọc đồ thị
+ Sử dụng biểu thức tính hiệu suất: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)
+ Sử dụng biểu thức tính công suất: \(P = {I^2}R\)
+ Sử dụng BĐT Cosi
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
