OA, OB là hai đoạn dây dẫn thẳng, ACB và OBD là hai dây dẫn hình nửa đường tròn đường kính AB và OB. Các đoạn dây dẫn này đồng tính và cùng tiết diện. Biết điện trở của OA và OB bằng nhau và bằng R. Tính điện trở giữa A và B (RAB )
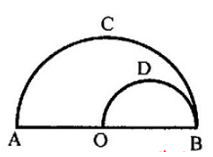
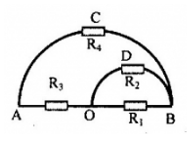
Gọi R1 = ROB = R, R2 = RODB, R3 = RAO = R, R4 = RACB
Từ hình vẽ, ta có:
((R1 // R2 ) nối tiếp R3 ) // R4
Ta có, dây dẫn tiết diện đều, đồng tính và điện trở của dây dẫn được xác định bằng biểu thức:
\(R = \rho \frac{l}{S}\)
\( \to \frac{{{R_2}}}{{{R_1}}} = \frac{{{l_2}}}{{{l_1}}} = \frac{{\pi \left( {\frac{{OB}}{2}} \right)}}{{OB}} \to {R_2} = \frac{{\pi R}}{2}\)
Ta có: R4 = 2R2 => R4 = πR
+ R1//R2 :
\({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{\frac{{\pi R}}{2}\pi R}}{{\frac{{\pi R}}{2} + \pi R}} = \frac{{\pi R}}{{\pi + 2}}\)
+ R12 nt R3:
\({R_{123}} = {R_{12}} + {R_3} = {R_{12}} = \frac{{\pi R}}{{\pi + 2}} + R = 2R\left( {\frac{{\pi + 1}}{{\pi + 2}}} \right)\)
+ R123 // R4:
\({R_{AB}} = \frac{{{R_{123}}{R_4}}}{{{R_{123}} + {R_4}}} = 2\pi R\left( {\frac{{\pi + 1}}{{{\pi ^2} + 4\pi + 2}}} \right) \approx 1,065R\)
Cho mạch điện như hình vẽ.
Biến trở AB là dây đồng chất, dài l = 1,3m, tiết diện S = 0,1mm2, điện trở suất 10-6Wm, U- hiệu điện thế không đổi. Nhận thấy khi con chạy ở các vị trí cách đầu A hoặc đầu B những đoạn như nhau bằng 40cm thì công suất tỏa nhiệt trên biến trở là như nhau. Xác định R0 ứng với vị trí của C.
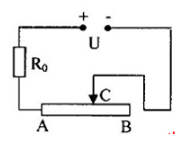
Gọi R1, R2 là điện trở của biến trở ứng với 2 vị trí trên của con chạyC; R là điện trở toàn phần của biến trở.
+ Điện trở toàn phần của biến trở:
\(R = \rho \frac{l}{S} = 13\Omega \to \left\{ \begin{array}{l}{R_1} = \frac{4}{{13}}R = 4\Omega \\{R_2} = \frac{9}{{13}}R = 9\Omega \end{array} \right.\)
+ Ta có:
\(\begin{array}{l}{P_1} = {P_2} \leftrightarrow {\left( {\frac{U}{{{R_0} + {R_1}}}} \right)^2}{R_1} = {\left( {\frac{U}{{{R_0} + {R_2}}}} \right)^2}{R_2}\\ \to {R_0} = \sqrt {{R_1}{R_2}} = 6\Omega \end{array}\)
Cho mạch điện như hình vẽ:
Biết R1 = 1$\Omega $, UPQ = 2V, RA = 0,5$\Omega $. Khi R4 = 6 thì IA = 0A. Tích R2.R3 là?
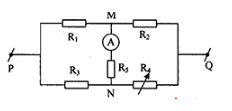
Khi R4 = 6$\Omega $ thì IA = 0, mạch trở thành mạch cầu cân bằng:
\(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}} \to {R_2}{R_3} = {R_1}{R_4} = 1.6 = 6\)
Có 3 điện trở R mắc như hình vẽ
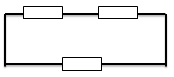
Điện trở của bộ là:
\(\left( {{R_1}nt{R_2}} \right)//{R_3} \Rightarrow {R_{_b}} = \dfrac{{\left( {R + R} \right).R}}{{3R}} = \dfrac{{2{{\rm{R}}^2}}}{{3R}} = \dfrac{{2R}}{3}\)
Để bóng đèn 120V – 60W sáng bình thường ở mạng điện có hiệu điện thế 220V người ta mắc nối tiếp nó với điện trở R, R có giá trị:
Cường độ dòng điện khi đèn sáng bình thường là:
\(I = \dfrac{P}{U} = \frac{{60}}{{120}} = 0,5{\rm{A}}\)
Ta có: \(P = \dfrac{{{U^2}}}{R} \Rightarrow R = \dfrac{{{U^2}}}{P} = \dfrac{{{{120}^2}}}{{60}} = 240\Omega \)
Đề bóng đèn sáng bình thường ở mạng điện có hiệu điện thế 220V thì:
\({R_{t{\rm{d}}}} = \dfrac{U}{I} = \dfrac{{220}}{{0,5}} = 440V\)
Suy ra phải mắc bóng đèn nối tiếp với điện trở phụ là:
\({R_p} = {R_{t{\rm{d}}}} - R = 440 - 240 = 200\Omega \)
Một nguồn điện có suất điện động \(E\) và điện trở trong \(r\) mắc với mạch ngoài là biến trở \(R\). Khi biến trở nhận các giá trị là \(4\,\,\Omega \) và \(1\,\,\Omega \) thì công suất tỏa nhiệt trên mạch ngoài đều bằng \(16\,\,W\). Tìm cường độ dòng điện khi nối tắt hai cực của nguồn điện.
Công suất tỏa nhiệt trên mạch ngoài là:
\(P = {I^2}R = \frac{{{E^2}R}}{{{{\left( {R + r} \right)}^2}}} = \frac{{{E^2}}}{{R + \frac{{{r^2}}}{R} + 2r}}\)
Khi điện trở mạch ngoài \({R_1} = 4\Omega \) và \({R_2} = 1\Omega \), mạch ngoài có cùng công suất, ta có:
\(\begin{array}{l}{P_1} = {P_2} \Rightarrow \frac{{{E^2}}}{{{R_1} + \frac{{{r^2}}}{{{R_1}}} + 2r}} = \frac{{{E^2}}}{{{R_2} + \frac{{{r^2}}}{{{R_2}}} + 2r}}\\ \Rightarrow {R_1} + \frac{{{r^2}}}{{{R_1}}} = {R_2} + \frac{{{r^2}}}{{{R_2}}} \Rightarrow {R_1} - {R_2} = {r^2}.\left( {\frac{1}{{{R_2}}} - \frac{1}{{{R_1}}}} \right)\\ \Rightarrow {R_1} - {R_2} = {r^2}.\frac{{{R_1} - {R_2}}}{{{R_1}.{R_2}}} \Rightarrow {R_1}{R_2} = {r^2}\\ \Rightarrow r = \sqrt {{R_1}{R_2}} = 2\,\,\left( \Omega \right)\end{array}\)
Công suất của mạch ngoài khi đó là:
\({P_1} = \frac{{{E^2}{R_1}}}{{{{\left( {{R_1} + r} \right)}^2}}} \Rightarrow 16 = \frac{{{E^2}.4}}{{{{\left( {4 + 2} \right)}^2}}} \Rightarrow E = 12\,\,\left( V \right)\)
Khi nối tắc hai cực của nguồn điện, cường độ dòng điện trong mạch là:
\(I = \frac{E}{r} = \frac{{12}}{2} = 6\,\,\left( A \right)\)
Biết rằng điện trở mạch ngoài của một nguồn điện tăng từ \({R_1} = 3\,\,\Omega \) đến \({R_2} = 10,5\,\,\Omega \) thì hiệu suất của nguồn tăng gấp \(2\) lần. Điện trở trong của nguồn bằng
Khi điện trở mạch ngoài là \({R_1};\,\,{R_2}\), hiệu suất của nguồn điện là:
\(\left\{ \begin{array}{l}{H_1} = \frac{{{R_1}}}{{{R_1} + r}}\\{H_2} = \frac{{{R_2}}}{{{R_2} + r}}\end{array} \right.\)
Theo đề bài ta có:
\(\begin{array}{l}{H_2} = 2{H_1} \Rightarrow \frac{{{R_2}}}{{{R_2} + r}} = 2\frac{{{R_1}}}{{{R_1} + r}}\\ \Rightarrow \frac{{10,5}}{{10,5 + r}} = \frac{{2.3}}{{3 + r}} \Rightarrow r = 7\,\,\left( \Omega \right)\end{array}\)

