Tổng hợp dao động điều hòa
Kỳ thi ĐGNL ĐHQG Hà Nội
Phát biểu nào sau đây là đúng khi nói về độ lệch pha giữa hai dao động:
Ta có:
+ 2 dao động cùng pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
+ 2 dao động ngược pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
+ 2 dao động vuông pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Biên độ dao động khi 2 dao động vuông pha:
\({A^2} = A_1^2 + A_2^2\)
Hai dao động điều hòa cùng phương có phương trình lần lượt là \({x_1} = 4\cos \left( {\pi t - \dfrac{\pi }{6}} \right)\left( {cm} \right)\) và \({x_2} = 4\cos \left( {\pi t - \dfrac{\pi }{2}} \right)\left( {cm} \right)\). Dao động tổng hợp của hai dao động này có biên độ là :
Biên độ dao động tổng hợp:
\({A^2} = A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \Delta \varphi \)
\( \Leftrightarrow A = \sqrt {{4^2} + {4^2} + 2.4.4.\cos \left| { - \dfrac{\pi }{6} + \dfrac{\pi }{2}} \right|} \)
\( \Leftrightarrow A = \sqrt {48} = 4\sqrt 3 \left( {cm} \right)\)
Hai dao động thành phần có biên độ là 4cm và 12cm. Biên độ dao động tổng hợp có thể nhận giá trị:
Biên độ dao động tổng hợp thỏa mãn điều kiện
\(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2} \Leftrightarrow 8 \le A \le 16\)
Vậy chỉ có A = 9cm thỏa mãn điều kiện trên
) Một vật khối lượng m = 500g được gắn vào đầu một lò xo nằm ngang. Vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số lần lượt có phương trình x1=6cos(10t+\(\frac{\pi }{2}\))(cm) và x2 = 8cos10t(cm). Năng lượng dao động của vật nặng bằng
Dao động của vật là tổng hợp hai dao động thành phần, có biên độ :
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}c{\rm{os}}\left( {{\varphi _1} - {\varphi _2}} \right)} = \sqrt {{6^2} + {8^2}} = 10cm\) = 0,1m
Tần số góc \(\omega \) = 10 rad/s
Vật có m = 500g = 0,5kg.
Năng lượng dao động của vật là:
\({\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,{5.10^2}.0,{1^2} = 0,25J\)
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = {\rm{ }}10cos\left( {2pt{\rm{ }} + {\rm{ }}\varphi } \right)\) cm và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{3})cm\). Khi năng lượng dao động của vật cực đại thì biên độ dao động A2 có giá trị là
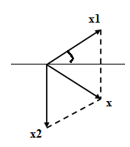
\(\begin{array}{l}\dfrac{{10}}{{\sin 30}} = \dfrac{{{A_2}}}{{\sin (60 + \varphi )}} = \dfrac{A}{{\sin (90 - \varphi )}}\\ \Rightarrow A = \dfrac{{10\sin (90 - \varphi )}}{{\sin 30}}\end{array}\)
Năng lượng dao động cực đại thì \({A_{max}} \Rightarrow \sin \left( {90 - \varphi } \right) = 1 \Rightarrow \varphi = 0\)
Khi đó: \(\left\{ \begin{array}{l}A = \dfrac{{10\sin 90}}{{\sin 30}} = 20cm\\{A_2} = \dfrac{{10.\sin 60}}{{\sin 30}} = 10\sqrt 3 cm\end{array} \right.\)
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số, biên độ \(A_1 = 4 cm\) và \(A_2 = 3 cm.\) Biên độ dao động tổng hợp đạt giá trị cực đại là
Biên độ dao động tổng hợp đạt giá trị cực đại là:
\({A_{\max }} = {A_1} + {A_2} = 4 + 3 = 7cm\)
Một vật có khối lượng m = 200g thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số và có các phương trình dao động là \({x_1} = 6.cos\left( {15t} \right)\,\left( {cm} \right)\) và \({x_2} = {A_2}.cos\left( {15t + \pi } \right)\,\left( {cm} \right)\). Biết cơ năng dao động của vật là \(W=0,05625J\). Biên độ \({A_2}\) nhận giá trị nào trong những giá trị sau:
Cơ năng dao động của vật:
\(\begin{array}{l}W = \dfrac{1}{2}m{\omega ^2}{A^2} \Leftrightarrow \dfrac{1}{2}.0,{2.15^2}.{A^2} = 0,05625\\ \Rightarrow A = 0,05m = 5cm\end{array}\)
Hai dao động ngược pha nên biên độ của dao động tổng hợp là:
\(A = \left| {{A_1} - {A_2}} \right| \Leftrightarrow 5 = \left| {6 - {A_2}} \right| \Rightarrow {A_2} = 1cm\)

