Hiện tượng phản xạ toàn phần
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho chiết suất của nước bằng 4/3, của benzen bằng 1,5; của thủy tinh flin là 1,8. Hiện tượng phản xạ toàn phần xảy ra khi chiếu ánh sáng từ:
Ta có, điều kiện để xảy ra hiện tượng phản xạ toàn phần là ánh sáng phải truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém (n1> n2)
=> Chọn A vì chiết suất của benzen > chiết suất của nước
Trong các ứng dụng sau đây, ứng dụng của hiện tượng phản xạ toàn phần là:
Hiện tượng phản xạ toàn phần được ứng dụng làm cáp quang để để truyền tín hiệu trong thông tin và để nội soi trong y học
Sợi quang trong cáp quang ứng dụng hiện tượng
Cáp quang là dây dẫn sáng ứng dụng phản xạ toàn phần để truyền tín hiệu trong thông tin và để nội soi trong y học
Nước có chiết suất 1,33. Chiếu ánh sáng từ nước ra ngoài không khí, góc có thể xảy ra hiện tượng phản xạ toàn phần là
Điều kiện để xảy ra phản xạ toàn phần là:
\(\left\{ \begin{gathered}
{n_2} < {n_1} \hfill \\
i \geqslant {i_{gh}} \hfill \\
\end{gathered} \right.\)
Góc giới hạn phản xạ toàn phần được xác định bởi công thức :
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,33}} \Rightarrow {i_{gh}} = {48^0}45'\)
Chiếu một tia sáng đơn sắc từ không khí vào một chất lỏng trong suốt dưới góc tới 450 thì góc khúc xạ là 300. Bây giờ, chiếu tia sáng đó từ chất lỏng ra không khí dưới góc tới i. Với giá trị nào của i để có tia khúc xạ ra ngoài không khí?
+ Khi chiếu tia sáng từ không khí vào chất lỏng:
\(\sin {45^0}\; = n.\sin {30^0} \Rightarrow n = \dfrac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \sqrt 2 \)
+ Khi chiếu tia sáng từ chất lỏng ra không khí. Góc giới hạn phản xạ toàn phần là:
\(\sin {i_{gh}} = \dfrac{1}{n} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^0}\)
Để có góc khúc xạ thì không xảy ra hiện tượng phản xạ toàn phần nên \(i < {45^0}\)
Một chùm tia sáng hẹp SI truyền trong mặt phẳng tiết diện vuông góc của một khối trong suốt như hình vẽ. Tia sáng phản xạ toàn phần ở mặt AC. Trong điều kiện đó, chiết n của khối trong suốt có giá trị như thế nào?
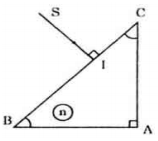
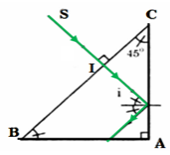
\(\Delta ABC\) vuông cân tại A \( \Rightarrow \widehat B = \widehat C = {45^0}\)
Có \(SI \bot BC \Rightarrow \)Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở I ở mặt khúc xạ AC: \(i = {45^0} \Rightarrow \sin i = \sin 45 = \dfrac{1}{{\sqrt 2 }}\)
Để tia sáng phản xạ toàn phần ở mặt AC thì:
\(i \ge {i_{gh}} \Leftrightarrow \sin i \ge \sin {i_{gh}} \Leftrightarrow \dfrac{1}{{\sqrt 2 }} \ge \dfrac{1}{n} \Rightarrow n \ge \sqrt 2 \)
Một khối bán trụ trong suốt có chiết suất \(n = 1,41 \approx \sqrt 2 \). Một chùm tia sáng hẹp nằm trong mặt phẳng của tiết diện vuông góc, chiếu tới khối bán trụ như hình vẽ. Xác định góc khúc xạ ló ra ngoài không khí. Biết α = 300.
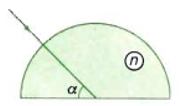

Ta có \(\alpha = {30^0} \Rightarrow i = {90^0} - \alpha = {60^0}\)
Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^0}\)
Ta có: \(i = {60^0} > {i_{gh}}\)
→ Xảy ra hiện tượng phản xạ toàn phần.
Một sợi quang hình trụ gồm phần lõi có chiết suất n=1,58 và phần vỏ bọc có chiết suất no=1,41. Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới α rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền trong phần lõi thì giá trị lớn nhất của góc α gần nhất với giá trị nào sau đây?
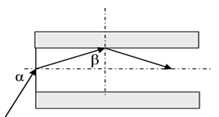
Ta có: \(\sin \left( {{i}_{gh}} \right)=\dfrac{{{n}_{0}}}{n}=\dfrac{1,41}{1,58}\Rightarrow {{i}_{gh}}=63,{{18}^{o}}\Rightarrow \beta \ge {{i}_{gh}}=63,{{18}^{o}}\)
\(\Rightarrow \) Góc khúc xạ tại mặt bên là \(r={{90}^{o}}-\beta \Rightarrow r\le 26,{{82}^{o}}\)
\(\sin \alpha =n\sin r\Rightarrow \alpha \le 45,{{48}^{o}}\approx {{45}^{o}}\)

