Câu hỏi:
2 năm trước
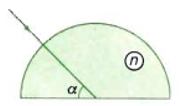
Một chùm tia sáng hẹp SI truyền trong mặt phẳng tiết diện vuông góc của một khối trong suốt như hình vẽ. Tia sáng phản xạ toàn phần ở mặt AC. Trong điều kiện đó, chiết n của khối trong suốt có giá trị như thế nào?
Trả lời bởi giáo viên
Đáp án đúng: a
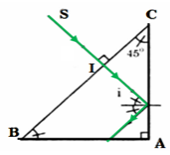
\(\Delta ABC\) vuông cân tại A \( \Rightarrow \widehat B = \widehat C = {45^0}\)
Có \(SI \bot BC \Rightarrow \)Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở I ở mặt khúc xạ AC: \(i = {45^0} \Rightarrow \sin i = \sin 45 = \dfrac{1}{{\sqrt 2 }}\)
Để tia sáng phản xạ toàn phần ở mặt AC thì:
\(i \ge {i_{gh}} \Leftrightarrow \sin i \ge \sin {i_{gh}} \Leftrightarrow \dfrac{1}{{\sqrt 2 }} \ge \dfrac{1}{n} \Rightarrow n \ge \sqrt 2 \)
Hướng dẫn giải:
+ Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)
+ Điều kiện để có phản xạ toàn phần: \(\left\{ \begin{array}{l}{n_2} < {n_1}\\i \ge {i_{gh}};\,\,\left( {\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}} \right)\end{array} \right.\)
Câu hỏi khác
- Bài tập thấu kính khoa học tự nhiên, công nghệ và khoa học xã hội ĐGNL có lời giải
- Bài tập định luật khúc xạ ánh sáng khoa học tự nhiên, công nghệ và khoa học xã hội ĐGNL HN có lời giải
- Bài tập hiện tượng phản xạ toàn phần khoa học tự nhiên, công nghệ và khoa học xã hội ĐGNL HN có lời giải
- Bài tập giao thoa ánh sáng - bài tập dịch nguồn, đặt bản mỏng khoa học tự nhiên, công nghệ và khoa học xã hội ĐGNL HN có lời giải
- Bài tập giao thoa ánh sáng đơn sắc khoa học tự nhiên, công nghệ và khoa học xã hội ĐGNL HN có lời giải
