Giao thoa ánh sáng - Bài tập dịch nguồn, đặt bản mỏng
Kỳ thi ĐGNL ĐHQG Hà Nội
Trong thí nghiệm I- âng về giao thoa ánh sáng đơn sắc, người ta thấy khoảng vân tăng thêm 0,3mm khi dời màn để khoảng cách giữa màn và hai khe thay đổi một đoạn 0,5m. Biết hai khe cách nhau là a = 1mm. Bước sóng của ánh sáng đã sử dụng là?
Gọi i và i’ là khoảng vân ban đầu và sau khi dời màn
D, D’ là khoảng cách giữa hai khe và màn lúc ban đầu và sau khi dời màn
Ta có:
+ Ban đầu: \(i = \dfrac{{\lambda D}}{a}\)
+ Khi dời màn : \(i' = \dfrac{{\lambda D'}}{a}\)
Mặt khác, theo đầu bài: Khoảng vân tăng thêm 0,3mm khi khoảng cách giữa màn và hai khe thay đổi 0,5m
=> \(D' > D \to D' = D + 0,5\)
\(\begin{array}{l}i' - i = 0,3mm = \Delta i \leftrightarrow \dfrac{{\lambda D'}}{a} - \dfrac{{\lambda D}}{a} = \Delta i\\ \leftrightarrow \dfrac{\lambda }{a}(D' - D) = \Delta i \to \lambda = \dfrac{{\Delta i.a}}{{D' - D}} = \dfrac{{0,{{3.10}^{ - 3}}{{.10}^{ - 3}}}}{{0,5}} = 0,{6.10^{ - 6}}m\end{array}\)
Một nguồn sáng đơn sắc λ chiếu vào một mặt phẳng chứa hai khe hở S1, S2 song song cách nhau một khoảng a và cách đều nguồn sáng. Đặt một màn ảnh song song và cách mặt phẳng chứa hai khe 1m. Đặt trước khe S1 một bản thủy tinh 2 mặt phẳng song song có chiết suất n , độ dày e. Khi đó, hệ thống vân sẽ dịch chuyển trên màn thế nào?
Khi đặt trước S1 một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :\({x_o}\, = \,\frac{{(n\, - \,1)eD}}{a}\) về phía S1
Một nguồn sáng đơn sắc \(\lambda = 0,6\mu m\) chiếu vào một mặt phẳng chứa hai khe hở S1, S2 hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn ảnh song song và cách mặt phẳng chứa hai khe 1m. Đặt trước khe S1 một bản thủy tinh 2 mặt phẳng song song có chiết suất n=1,5; độ dày \(e = 12\mu m\). Vị trí hệ thống vân sẽ dịch chuyển trên màn thế nào?
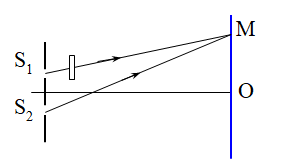
Khi đặt trước S1 một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :\({x_0} = \frac{{(n - 1)eD}}{a} = \frac{{(1,5 - 1){{.12.10}^{ - 6}}.1}}{{{{10}^{ - 3}}}} = {6.10^{ - 3}}m = 6mm\) về phía S1
Trong thí nghiệm I-âng cho a = 2mm, D = 2,2m. Người ta đặt trước khe sáng S1 một bản mặt song song mỏng chiết suất n, bề dày \(e = 6\mu m\) . Khi đó, ta thấy hệ thống vân giao thoa trên màn bị dịch chuyển một đoạn 3mm về phía S1. Chiết suất n của chất làm bản mỏng là:
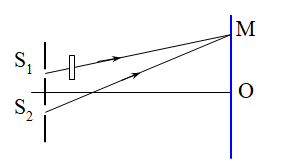
Khi đặt trước S1 một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :\({x_0} = \frac{{(n - 1)eD}}{a}\)về phía S1
Theo đầu bài, ta có: \({x_0} = 3mm = \frac{{(n - 1)eD}}{a} \to n = \frac{{a{x_0}}}{{eD}} + 1 = \frac{{{{2.10}^{ - 3}}{{.3.10}^{ - 3}}}}{{{{6.10}^{ - 6}}.2,2}} + 1 \approx 1,46\)
Trong thí nghiệm I-âng cho a=2,5mm, D=1,5m. Người ta đặt trước một trong hai khe sáng một bản mặt song song mỏng chiết suất n=1,52. Khi đó, ta thấy hệ vân giao thoa trên màn bị dịch chuyển một đoạn 3mm. Bề dày e của bản mỏng là:
Giả sử đặt trước S1 bản mặt song song, ta có:
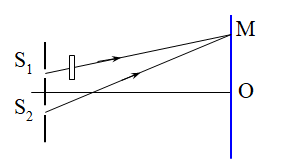
Khi đặt trước S1 một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :\({x_0} = \frac{{(n - 1)eD}}{a}\) về phía S1
Theo đầu bài, ta có: \({x_0} = 3mm = \frac{{(n - 1)eD}}{a} \to e = \frac{{a{x_0}}}{{(n - 1)D}} = \frac{{2,{{5.10}^{ - 3}}{{.3.10}^{ - 3}}}}{{(1,52 - 1).1,5}} \approx 9,{62.10^{ - 6}}m = 9,62\mu m\)
Một nguồn sáng đơn sắc \(\lambda = 0,6\mu m\)chiếu vào một mặt phẳng chứa hai khe S1 và S2 , hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn hứng ảnh song song và cách mặt phẳng chứa hai khe 1m. Ban đầu đặt sau khe S2 một bản thủy tinh song song có chiết suất n; độ dày e. Sau đó, không đặt bản thủy tinh mà đổ đầy vào khoảng giữa khe và màn một chất lỏng có chiết suất n’. Người ta thấy khoảng cách giữa hai vân sáng liên tiếp bằng 0,45mm. Tính chiết suất n’
Ta có, khoảng cách giữa 2 vân sáng liên tiếp là i = 0,45mm
\(i = \frac{{\frac{\lambda }{{n'}}D}}{a} \to n' = \frac{{\lambda D}}{{ia}} = \frac{{0,{{6.10}^{ - 6}}.1}}{{0,{{45.10}^{ - 3}}{{.10}^{ - 3}}}} = \frac{4}{3}\)
Đặt một mảnh mica phẳng có chiết suất n =1,6 che một trong hai khe của thí nghiệm I-âng, ta thấy vân sáng bậc 30 dịch chuyển đến vị trí của vân sáng chính giữa. Nếu bước sóng của ánh sáng là \(\lambda = 450nm\) thì độ dày của mảnh mica là:
Giả sử đặt trước S1 mảnh mica phẳng, ta có:
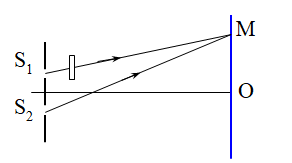
Ta có: Khi đặt trước S1 bản mica thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :
\({x_0} = \frac{{(n - 1)eD}}{a}\) về phía S1
Theo đầu bài ta có: đoạn dịch chuyển này bằng 30i
\(\begin{array}{l}{x_0} = 30i \leftrightarrow \frac{{(n - 1)eD}}{a} = 30i = \frac{{30\lambda D}}{a}\\ \to e = \frac{{30\lambda }}{{(n - 1)}} = \frac{{{{30.450.10}^{ - 9}}}}{{(1,6 - 1)}} = 2,{25.10^{ - 5}}m = 22,5\mu m\end{array}\)
Trong thí nghiệm I-âng về giao thoa ánh sáng, một nguồn sáng đơn sắc có bước sóng λ chiếu vào một mặt phẳng chứa hai khe hở S1, S2 hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn ảnh song song và cách mặt phẳng chứa hai khe 1m. Đặt trước khe S1 một bản thủy tinh 2 mặt phẳng song song có chiết suất n = 1,5, độ dày \(e{\rm{ }} = 12\mu m\) . Người ta đo được độ dịch chuyển của vân trung tâm bằng khoảng cách giữa 9 vân sáng liên tiếp. Bước sóng ánh sáng dùng trong thí nghiệm là?
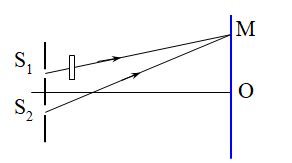
Ta có: Khi đặt trước S1 một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :\({x_0} = \frac{{(n - 1)eD}}{a}\) về phía S1
Theo đầu bài, ta có: khoảng dịch chuyển đó bằng khoảng cách giữa 9 vân sáng liên tiếp
Ta có, khoảng cách giữa 9 vân sáng liên tiếp là: 8i
\(\begin{array}{l} \to {x_0} = 8i \leftrightarrow \frac{{(n - 1)eD}}{a} = 8\frac{{\lambda D}}{a}\\ \to \lambda = \frac{{(n - 1)e}}{8} = \frac{{(1,5 - 1){{.12.10}^{ - 6}}}}{8} = 0,{75.10^{ - 6}}m = 0,75\mu m\end{array}\)

