Công suất tiêu thụ của mạch điện xoay chiều - Hệ số công suất

Ta có:

+ Cảm kháng:

\({Z_L} = \omega L = 2\pi fL = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \)

+ Dung kháng:

\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)

+ Tổng trở của mạch:

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = \sqrt {{{80}^2} + {{(40 - 100)}^2}}  = 100\Omega \)

+ Cường độ dòng điện hiệu dụng trong mạch:

 \(I = \dfrac{U}{Z} = \dfrac{{220}}{{100}} = 2,2(A)\)

+ Công suất tỏa nhiệt :

 \(P = {I^2}R = {2,2^2}.80 = 387,2{\rm{W}}\)

Ta có:

+ Dung kháng:

 \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80\Omega \)

+ Tổng trở của mạch:

\(Z = \sqrt {{R^2} + {Z_C}^2}  = \sqrt {{{60}^2} + {{80}^2}}  = 100\Omega \)

+ hệ số công suất:

\({\rm{cos}}\varphi  = \dfrac{R}{Z} = \dfrac{{60}}{{100}} = 0,6\)

Ta có: \(\left( {{u_d},u} \right) = 1,56rad = \frac{\pi }{2};U = 6V;{U_d} = 10V\)

Vì điện áp hai đầu cuộn dây lệch pha với điện áp hai đầu đoạn mạch góc 1,56rad nên cuộn dây có điện trở thuần.

Ta có giản đồ vecto:

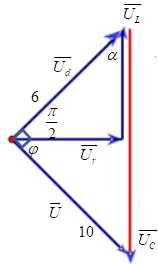
Từ giản đồ vecto ta có: \(\tan \alpha  = \frac{6}{{10}} = 0,6\)

\( \Rightarrow \alpha  = shif\tan 0,6 = 0,54042\) \( \Rightarrow \cos \alpha  = 0,86\)

Mà \(\alpha  = \varphi  \Rightarrow \cos \varphi  = 0,86\)

Công suất tiêu thụ của đoạn mạch \(AB\) là:

 \(P = \dfrac{{{U^2}}}{R}.co{s^2}\varphi  = \dfrac{{{{220}^2}}}{{100}}.{\left( {\cos \dfrac{\pi }{3}} \right)^2} = 121W\)

Ta có: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)

Từ đồ thị ta có tại \(R = 3\Omega \) thì \(H = 0,75\)

\( \Leftrightarrow \frac{R}{{R + r}} = 0,75 \Leftrightarrow \frac{3}{{3 + r}} = 0,75 \Rightarrow r = 1\Omega \)

Công suất tiêu thụ trên R:

\({P_R} = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R = \frac{{{E^2}}}{{{{\left( {\sqrt R  + \frac{r}{{\sqrt R }}} \right)}^2}}}\)

\( \Rightarrow {P_{Rma{\rm{x}}}}\) khi \({\left( {\sqrt R  + \frac{r}{{\sqrt R }}} \right)^2}_{\min }\)

Áp dụng BĐT Cosi ta có: \(\sqrt R  + \frac{r}{{\sqrt R }} \ge 2\sqrt r  = 2\)

\( \Rightarrow \sqrt R  + \frac{r}{{\sqrt R }} = 2\sqrt r  = 2\) khi \(\sqrt R  = \frac{r}{{\sqrt R }}\)hay \(R = r\)

\( \Rightarrow {P_{R\max }} = \frac{{{E^2}}}{{4{\rm{R}}}} = \frac{{{E^2}}}{{4{\rm{r}}}} = \frac{{{6^2}}}{4} = 9W\)

Từ đồ thị ta có:

Khi \(\varphi  = 0 \to {P_{ma{\rm{x}}}} = {P_0} = \frac{{{U^2}}}{R}\,\,\,\,\left( 1 \right)\)

Khi \(\varphi  = {\varphi _1} \to P = \frac{3}{4}{P_0} = UI\cos \varphi  = \frac{{{U^2}}}{{{Z^2}}}R\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta suy ra: \(\frac{3}{4}\frac{{{U^2}}}{R} = \frac{{{U^2}}}{{{Z^2}}}R\)

\( \Rightarrow 3{{\rm{Z}}^2} = 4{{\rm{R}}^2} \Leftrightarrow 3\left( {{R^2} + Z_L^2} \right) = 4{{\rm{R}}^2} \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\)

Lại có: \(\tan {\varphi _1} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow {\varphi _1} = \frac{\pi }{6}\) rad

Cường độ dòng điện hiệu dụng trong mạch là:

\(I = \dfrac{P}{{U\cos \varphi }} = \dfrac{{1200}}{{220.1}} = \dfrac{{60}}{{11}} \approx 5,45\left( A \right)\)