Con lắc lò xo
Kỳ thi ĐGNL ĐHQG Hà Nội
Một con lắc lò xo dao động theo phương ngang với cơ năng dao động là 20mJ và lực đàn hồi cực đại là 2N. Biên độ dao động của con lắc là
Ta có:
- Cơ năng dao động:
\({\rm{W}} = \dfrac{1}{2}k{A^2} = {20.10^{ - 3}}J\)
- Lực đàn hồi cực đại: Fđhmax = kA = 2N
\( \to \dfrac{{\rm{W}}}{{{F_{{\rm{d}}{{\rm{h}}_{{\rm{max}}}}}}}} = \dfrac{A}{2} = \dfrac{{{{20.10}^{ - 3}}}}{2} \\\to A = 0,02m = 2cm\)
Chu kì dao động của con lắc lò xo phụ thuộc vào:
Ta có, chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
=> chu kì T phụ thuộc vào khối lượng m, độ cứng k
Đồ thị nào sau đây biểu diễn đúng sự phụ thuộc của chu kì vào khối lượng của con lắc lò xo dao động điều hòa?

Ta có, chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \to {T^2} = 4{\pi ^2}\dfrac{m}{k}\)
=> Đồ thị $T - m$ có dạng parabol
Một con lắc lò xo dao động điều hòa. Phát biểu nào sau đây là sai?
A - sai vì: Động năng của con lắc lò xo:
\(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\)
B, C, D - đúng
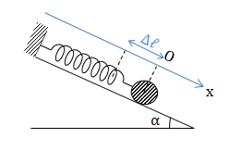
Một con lắc lò xo đặt nằm nghiêng như hình vẽ, vật nặng có khối lượng m, lò xo có độ cứng k. Độ dãn của lò xo tại vị trí cân bằng và chu kì dao động của con lắc lò xo là:
Ta có:
Độ dãn của con lắc lò xo nằm ngang tại vị trí cân bằng: \(\Delta l = \frac{{mg\sin \alpha }}{k}\)
Chu kì do động của con lắc lò xo nằm ngang:
\({\rm{ }}T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta l}}{{g\sin \alpha }}} \)
Một con lắc lò xo dao động điều hòa với biên độ $A$, tần số góc $ω$. Li độ và vận tốc của vật khi $W_d=nW_t$ là:
Tại vị trí có động năng gấp n lần thế năng của vật: Wđ = nWt
\(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm \dfrac{A}{{\sqrt {n + 1} }}\\v = \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)
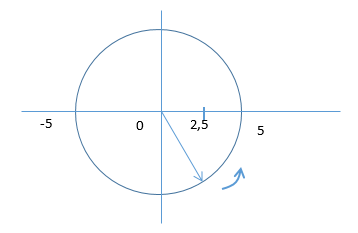
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt - π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t = 0, lực đàn hồi đổi chiều lần đầu tại thời điểm:
Từ phương trình dao động, ta có chu kì dao động: \(T = \dfrac{{2\pi }}{\omega } = 1{\rm{s}}\)
Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = 5c{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = 2,5cm\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
Lực đàn hồi đổi chiều tại vị trí cân bằng
Từ vòng tròn lượng giác,
=> Lực đàn hồi đổi chiều lần đầu kể từ t = 0 tại thời điểm: \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}} = \dfrac{5}{{12}}s\)
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t + \pi /3)cm$ . Tại thời điểm mà thế năng bằng $3$ lần động năng thì vật có tốc độ là:
Từ phương trình dao động điều hòa, ta có:
+ Biên độ A = 10 cm
+ Tần số góc: ω = 4p
Khi Wđ = 3Wt
\(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to {W_d} = \dfrac{1}{{3 + 1}}W \to v = \pm \dfrac{{A\omega }}{{\sqrt {3 + 1} }} = \pm 20\pi cm/s\)
Một con lắc lò xo dao động điều hoà theo phương thẳng đứng. Trong quá trình dao động của vật, chiều dài của lò xo thay đổi từ 20 cm đến 28 cm. Biên độ dao động của vật là
Chiều dài quỹ đạo chuyển động của con lắc là:
\(L = {l_{max}}-{l_{min}} = 2A \Rightarrow A = \frac{{{l_{\max }} - {l_{\min }}}}{2} = \frac{{28 - 20}}{2} = 4\,\,\left( {cm} \right)\)
Một vật có khối lượng $400g$ dao động điều hòa có đồ thị động năng như hình vẽ. Tại thời điểm $t = 0$ vật đang chuyển động theo chiều dương, lấy $\pi^2=10$. Phương trình dao động của vật là:
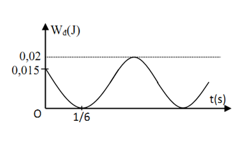
Từ đồ thị, ta có:
+ Tại thời điểm ban đầu (t =0) :
\(\begin{array}{l}{{\rm{W}}_d} = 0,015 \to {{\rm{W}}_t} = 0,02 - 0,015 = {5.10^{ - 3}}J = \dfrac{{\rm{W}}}{4}\\ \to {x_0} = \pm \dfrac{A}{2}\end{array}\)
+ Vị trí có Wđ = 0 lần thứ nhất: <=> x1 = ±A
Dựa vào đồ thị ta suy ra: x0 = A/2 và x1 = A
=> Khoảng thời gian vật đi từ x0 đến x1 là:
\(\Delta t = \dfrac{T}{6} = \dfrac{1}{6}s \to T = 1{\rm{s}} \to \omega = \dfrac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\)
\({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2} = 0,02 \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.0,02}}{{0,4.{{(2\pi )}^2}}}} = 0,05m = 5cm\)
Tại t = 0:
\(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi {\rm{ = }}\dfrac{A}{2}\\v = - {\rm{Asin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
=> Phương trình dao động của vật: \(x = 5c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{3}} \right)cm\)
Một con lắc lò xo gồm vật nhỏ khối lượng \(m\) và lò xo có độ cứng \(k\) đang dao động điều hòa với biên độ \(A\).Tốc độ cực đại của vật là:
Tốc độ góc của con lắc: \(\omega = \sqrt {\dfrac{k}{m}} \)
Tốc độ cực đại của vật là \({v_{{\rm{max}}}} = \omega A = A.\sqrt {\dfrac{k}{m}} \)
Con lắc lò xo dao động điều hòa trên mặt phẳng ngang không ma sát. Khi vật ở vị trí biên, ta giữ chặt một phần của lò xo làm cơ năng của vật giảm \(10\% \) thì biên độ dao động của hệ vật sẽ
Cơ năng ban đầu của con lắc là: \({\rm{W}} = \dfrac{1}{2}k{A^2}\)
Giữ chặt một phần của lò xo, biên độ mới của con lắc và độ cứng của lò xo:
\(k'A' = kA \Rightarrow k' = \dfrac{{kA}}{{A'}}\)
Cơ năng của con lắc giảm 10%, cơ năng còn lại là:
\(\begin{array}{l}{\rm{W}}' = \dfrac{1}{2}k'A{'^2} = 0,9W = 0,9.\dfrac{1}{2}k{A^2}\\ \Rightarrow \dfrac{{kA}}{{A'}}.A{'^2} = 0,9.k{A^2} \Rightarrow A' = 0,9A = A.90\% \\ \Rightarrow A - A' = A.10\% \end{array}\)
Một vật nặng gắn vào một lò xo nhẹ có độ cứng k = 20 N/m thực hiện dao động điều hoà với biên độ A = 5cm. Động năng của vật khi nó cách vị trí cân bằng 4 cm là
Áp dụng định lí bảo toàn cơ năng cho con lắc, ta có:
\(\begin{align}& \text{W}={{\text{W}}_{t}}+{{\text{W}}_{d}}\Rightarrow \frac{1}{2}k{{A}^{2}}=\frac{1}{2}k{{x}^{2}}+{{\text{W}}_{d}} \\& \Rightarrow {{\text{W}}_{d}}=\frac{1}{2}k{{A}^{2}}-\frac{1}{2}k{{x}^{2}}=0,009\,\,\left( J \right) \\\end{align}\)
Xét một con lắc lò xo gồm vật nhỏ và lò xo nhẹ dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Chọn gốc thế năng tại vị trí cân bằng. Tại vị trí con lắc có động năng bằng cơ năng, li độ của vật có giá trị là:
Ta có:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
\( \Leftrightarrow \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{{\rm{x}}^2}\)
Tại VTCB thế năng bằng 0.
Vị trí con lắc có động năng bằng cơ năng => là vị trí động năng cực đại => VTCB.
Tại VTCB, li độ x = 0.
Xét một con lắc lò xo đang dao động điều hoà. Gọi T là khoảng thời gian nhỏ nhất giữa hai lần liên tiếp vật nặng có độ lớn vận tốc cực đại. Chu kì con lắc này bằng:
Gọi T’ là chu kì của con lắc lò xo.
Khoảng thời gian nhỏ nhất giữa hai lần liên tiếp vật nặng có độ lớn vận tốc cực đại là $\frac{T'}{2}$
Ta có: $\frac{{{T}'}}{2}=T\Rightarrow {T}'=2T.$
Đề thi THPT QG - 2020
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ và vật nhỏ A có khối lượng m. Lần lượt treo thêm các quả cân vào A thì chu kì dao động điều hòa của con lắc tương ứng là T. Hình bên biểu diễn sự phụ thuộc của T2 theo tổng khối lượng \(\Delta m\) của các quả cân treo vào A. Giá trị của m là
Ta có, chu kì dao động của con lắc tại các vị trí \(\Delta m\) là: \(T = 2\pi \sqrt {\frac{{m + \Delta m}}{k}} \)
Từ đồ thị, ta có:
+ Tại \(\Delta {m_{10}} = 10g\) ta có: \(T_{10}^2 = 0,3{s^2}\)
+ Tại \(\Delta {m_{30}} = 30g\) ta có: \(T_{30}^2 = 0,4{s^2}\)
Mặt khác: \(\left\{ \begin{array}{l}{T_{10}} = 2\pi \sqrt {\frac{{m + \Delta {m_{10}}}}{k}} \\{T_{30}} = 2\pi \sqrt {\frac{{m + \Delta {m_{30}}}}{k}} \end{array} \right.\) \( \Rightarrow \frac{{T_{10}^2}}{{T_{30}^2}} = \frac{{m + \Delta {m_{10}}}}{{m + \Delta {m_{30}}}} = \frac{{0,3}}{{0,4}} \Leftrightarrow \frac{{m + 10}}{{m + 30}} = \frac{3}{4} \Rightarrow m = 50g\)

