Điện trường

Ta có:

+ Cường độ điện trường giữa hai bản tụ điện là:

 \(E = \dfrac{U}{d} = \dfrac{{110}}{{0,05}} = 2200V/m\).

+ Lực điện trường tác dụng lên điện tích là \(F = qE = 1,{6.10^{ - 19}}.2200 = 3,{52.10^{ - 16}}N\).

+ Định luật II Niuton có \(F = ma\) 

=> điện tích di chuyển trong điện trường với gia tốc \(a = \dfrac{F}{m} = \dfrac{{3,{{52.10}^{ - 16}}}}{{1,{{67.10}^{ - 27}}}} = 2,{11.10^{11}}m/{s^2}\) 

\( \to v_N^2 - v_M^2 = 2as \\\Rightarrow {v_N} = \sqrt {2.2,{{11.10}^{11}}.\left( {0,03} \right) + {{\left( {{{2.10}^5}} \right)}^2}}  \\= 2,{3.10^5}m/s\).

Ta có,

    + Cường độ điện trường E không phụ thuộc vào điện tích thử q

    + Lực điện: $F = k\frac{{\left| {qQ} \right|}}{{\varepsilon {r^2}}}$

=> Khi q tăng lên gấp đôi thì, E không đổi và F tăng gấp đôi

Ta có :

\(\overrightarrow {{E_2}}  = 2\overrightarrow {{E_1}} \)=> \(\overrightarrow {{E_2}}  \uparrow  \uparrow \overrightarrow {{E_1}} \)=> điểm C thuộc đường thẳng AB

Lại có q₁ và q₂ trái dấu => C nằm trong đoạn AB

=> CA + CB = AB = 30cm.               (1)

Mặt khác,

\(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{C{A^2}}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{C{B^2}}}\end{array} \right. \to \frac{{{E_1}}}{{{E_2}}} = \frac{{\left| {{q_1}} \right|C{B^2}}}{{\left| {{q_2}} \right|C{A^2}}} = \frac{1}{2} \to \frac{{CA}}{{CB}} = \sqrt {2\frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}}  = \sqrt {2\frac{{\left| {{{10}^{ - 9}}} \right|}}{{\left| { - {{8.10}^{ - 9}}} \right|}}}  = \frac{1}{2}\)  (2)

Từ (1) và (2) ta suy ra: CA = 10cm, CB = 20cm

Ta có:

Gia tốc:

\(a =  - \dfrac{{qE}}{m} =  - \dfrac{{1,{{6.10}^{ - 19}}.3000}}{{1,{{67.10}^{ - 27}}}} =  - 2,{87.10^{ - 11}}\) (dấu “-” do proton chuyển động ngược chiều \(\overrightarrow E \))

Áp dụng công thức độc lập với thời gian:

\({v^2} - v_0^2 = 2{\rm{a}}s \Leftrightarrow v = \sqrt {2.( - 2,{{87.10}^{11}}).0,03 + {{\left( {{{4.10}^5}} \right)}^2}}  = 3,{78.10^5}m/s\)

Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \)lần lượt là cường độ điện trường do q₁ và q₂ gây ra tại M.

Theo đề bài ta có:

\(\overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  = 0 \to \overrightarrow {{E_1}}  = \overrightarrow { - {E_2}}  \to \overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}} \)=> M phải thuộc AB

Và vì 2 điện tích cùng dấu => M phải ở bên trong AB

Mặt khác: \(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon M{A^2}}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon M{B^2}}}\end{array} \right. \to \frac{{{E_1}}}{{{E_2}}} = \frac{{\left| {{q_1}} \right|M{B^2}}}{{\left| {{q_2}} \right|M{A^2}}} = 1 \to \frac{{MA}}{{MB}} = \sqrt {\frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}}  = \sqrt {\frac{{\left| {{{4.10}^{ - 6}}} \right|}}{{\left| {{{36.10}^{ - 6}}} \right|}}}  = \frac{1}{3}\)

Lại có: MA + MB = 16

=> MA = 4cm, MB = 12cm

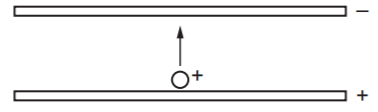
Nhận xét: điện trường giữa hai tấm kim lại tích điện trái dấu là điện trường đều có cường độ E

Lực điện tác dụng lên điện tích là:

\(F = \left| q \right|E = ma \Rightarrow a = \frac{{\left| q \right|E}}{m}\)

Chuyển động của điện tích có phương trình là:

\({v^2} - {v_0}^2 = 2ax \Rightarrow {v^2} = 2ax = 2\frac{{\left| q \right|E}}{m}x\)

Động năng của hạt là:

\({E_k} = \frac{1}{2}m{v^2} = \frac{1}{2}.m.2\frac{{\left| q \right|E}}{m}x = \left| q \right|Ex\)

→ Đồ thị động năng E_k theo quãng đường x là đường thẳng đi qua gốc tọa độ

Điện tích dương chuyển động từ nơi có điện thế cao đến nơi có điện thế thấp.

Điện tích âm chuyển động từ nơi có điện thế thấp đến nơi có điện thế cao.

Proton mang điện tích dương.

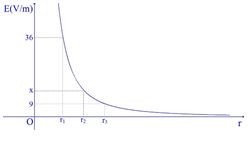
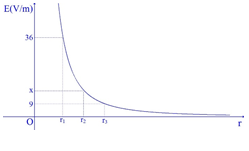
Ta có:  \(E = \dfrac{{k\left| Q \right|}}{{{r^2}}} \Rightarrow E\sim\dfrac{1}{{{r^2}}} \Leftrightarrow r\sim\dfrac{1}{{\sqrt E }}\) 

\( \Rightarrow {r_2} = \dfrac{{{r_1} + {r_3}}}{2} \Rightarrow \dfrac{2}{{\sqrt {{E_2}} }} = \dfrac{1}{{\sqrt {{E_1}} }} + \dfrac{1}{{\sqrt {{E_3}} }} \Rightarrow {E_2} = x = 16\) (V/m)

Ta có: \(F = qE = 1,{6.10^{ - 19}}.200 = 3,{2.10^{ - 17}}N\)

Do electron mang điện tích âm nên \(\overrightarrow F  \uparrow  \downarrow \overrightarrow E \) => \(\overrightarrow F \) hướng thẳng đứng từ dưới lên.

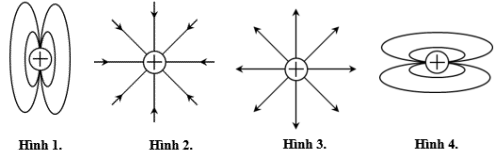
Đường sức điện của điện tích dương là các đường thẳng có hướng đi từ điện tích dương ra vô cực.

\( \Rightarrow \) Hình 3 biểu diễn đường sức điện của điện tích dương.

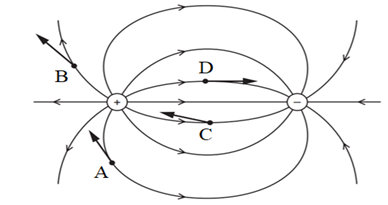
Nhận xét: vecto cường độ điện trường có hướng trùng với hướng của tiếp tuyến trên đường sức điện

Lực điện tác dụng lên electron có chiều ngược chiều vecto cường độ điện trường

→ Lực tác dụng lên electron tại vị trí A đúng

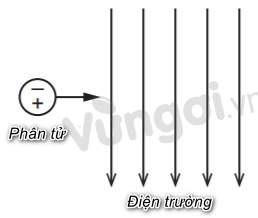
Trước khi vào điện trường, phân tử chuyển động với vận tốc không đổi theo phương ngang → vận tốc theo phương ngang không đổi, vận tốc theo phương thẳng đứng bằng 0

Nhận xét: lực điện tác dụng lên điện tích dương hướng thẳng đứng xuống

Lực điện tác dụng lên điện tích âm hướng thẳng đứng lên

Hai điện tích có độ lớn bằng nhau → tổng hợp lực tác dụng lên phân tử bằng 0

→ vận tốc theo phương thẳng đứng bằng 0

Quả cầu chịu tác dụng của lực căng \(\overrightarrow T \), trọng lực \(\overrightarrow P \) và lực điện trường \(\overrightarrow F \).

Lực căng \(\overrightarrow T \) và trọng lực \(\overrightarrow P \) là hai lực cân bằng.

Suy ra, độ lớn lực điện trường tác dụng lên quả cầu là:

\(F = E.q = {10^6}{.5.10^{ - 9}} = {5.10^{ - 3}}N\)