Bài tập sóng cơ
Kỳ thi ĐGNL ĐHQG Hà Nội
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục $Ox$. Tại thời điểm $t_0$ một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử $M$ và $O$ dao động lệch pha nhau?
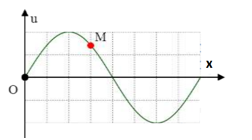
Từ đồ thị ta có:
+ Bước sóng \(\lambda = 8\) ô
+ Khoảng cách từ O đến M là \(\Delta x = 3\) ô
=> Độ lệch pha giữa M và O là: \(\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = 2\pi .\dfrac{3ô}{8 ô} = \dfrac{{3\pi }}{4}rad\)
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
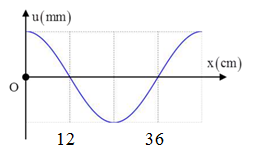
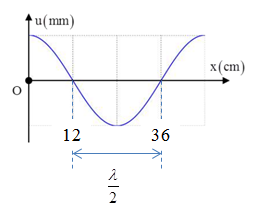
Từ đồ thị ta có:
\(\dfrac{\lambda }{2} = 36 - 12 = 24 \to \lambda = 48cm\)
Một sóng ngang hình sin truyền trên một sợi dây dài. Chu kì của sóng cơ này là 3s. Ở thời điểm t, hình dạng một đoạn của sợi dây như hình vẽ. Các vị trí cân bằng của các phần tử dây cùng nằm trên trục Ox. Tốc độ lan truyền của sóng cơ này là:
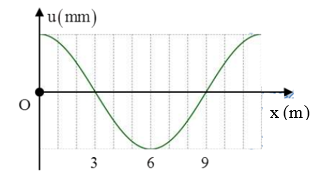
Từ đồ thị ta có:
\(\frac{\lambda }{2} = 9 - 3 = 6 \to \lambda = 12m\)
Tốc độ lan truyền sóng:
\(v = \frac{\lambda }{T} = \frac{{12}}{3} = 4m/s\)
Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó, điểm N đang chuyển động:
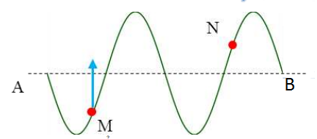
Theo phương truyền sóng, các phần tử trước đỉnh sóng sẽ đi xuống, sau đỉnh sóng sẽ đi lên.
Từ đồ thị ta có, điểm M sau đỉnh sóng đang đi lên
=> Sóng truyền từ B đến A và N cũng đang đi lên
Một sóng hình sin đang truyền trên một sợi dây, theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở các thời điểm t1 và t2 = t1 + 0,3s. Chu kì của sóng là:
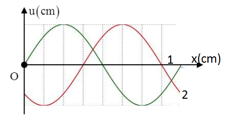
Từ đồ thị dao động sóng ta có: ∆x = 3ô; λ = 8ô
Vận tốc truyền sóng:
\(v = \frac{{\Delta x}}{{\Delta t}} = \frac{{3ô }}{{0,3}}\)
Chu kì dao động sóng:
\(T = \frac{\lambda }{v} = \frac{{8ô }}{{\frac{{3ô }}{{0,3}}}} = 0,8{\rm{s}}\)
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm $t$, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục $Ox$. Bước sóng của sóng này bằng:
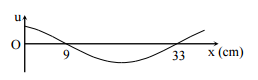
Từ đồ thị, ta có:
\(\dfrac{\lambda }{2} = 33 - 9 = 24cm \to \lambda = 48cm\)
Một nguồn phát sóng dao động theo phương trình \(u = ac{\rm{os20}}\pi {\rm{t}}\) (cm). Trong khoảng thời gian 2s sóng truyền đi được quãng đường bằng bao nhiêu lần bước sóng?
Ta có:
\(T = \dfrac{{2\pi }}{{20\pi }} = 0,1s\)
2s = 20T
=> Quãng đường sóng truyền đi trong 2s bằng 20 lần bước sóng
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số $500Hz$. Người ta thấy hai điểm $A, B$ trên sợi dây cách nhau $200cm$ dao động cùng pha và trên đoạn dây $AB$ có hai điểm khác dao động ngược pha với $A$. Tốc độ truyền sóng trên dây là:
2 điểm A, B dao động cùng pha và trên AB có 2 điểm khác dao động ngược pha với A.
\( \to AB = 2\lambda = 200cm \to \lambda = 100cm\)
Ta có tốc độ truyền sóng:
\(v = \lambda f = 100.500 = 50000cm/s = 500m/s\)
Một sóng ngang có chu kì $T = 0,2s$ truyền trong một môi trường đàn hồi có tốc độ $1 m/s$. Xét trên phương truyền sóng $Ox$, vào một thời điểm nào đó một điểm $M$ nằm tại đỉnh sóng thì ở trước $M$ theo chiều truyền sóng, cách $M$ một khoảng từ $42cm$ đến $60cm$ có điểm $N$ đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách $MN$ là:
Bước sóng:
\(\lambda = vT = 1.0,2 = 0,2m\)
Độ lệch pha:
Khi điểm M ở đỉnh sóng, điểm N ở vị trí cân bằng đang đi lên
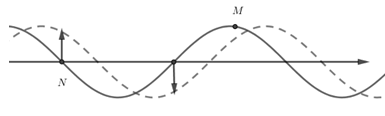
Theo hình vẽ thì khoảng cách MN
\(MN = \dfrac{3}{4}\lambda + k\lambda \) với $k = 0; 1; 2; ...$
\(\begin{array}{l}0,42 < MN = \dfrac{3}{4}\lambda + k\lambda < 0,60 \to 1,35 < k < 2,25\\ \to k = 2\\ \to MN = \dfrac{3}{4}\lambda + 2\lambda = 0,55m = 55cm\end{array}\)
Sóng truyền từ điểm M đến điểm O rồi đến điểm N trên cùng một phương truyền sóng với tốc độ \(v = 20m/s\). Cho biết tại O dao động có phương trình \({u_O} = 4cos\left( {2\pi f - \dfrac{\pi }{2}} \right)cm\) và tại hai điểm gần nhau nhất cách nhau \(6m\) trên cùng phương truyền sóng thì dao động lệch pha nhau góc \(\dfrac{{2\pi }}{3}rad\). Cho \(ON = 50cm\). Phương trình sóng tại N là
+ Độ lệch pha giữa hai điểm gần nhau nhất cách nhau \(6m\) trên phương truyền sóng dao động lệch pha nhau \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi }}{3}\)
\( \Rightarrow \lambda = \dfrac{{2\pi .6}}{{\dfrac{{2\pi }}{3}}} = 18m\)
Lại có: \(\lambda = \dfrac{v}{f} \Rightarrow f = \dfrac{v}{\lambda } = \dfrac{{20}}{{18}} = \dfrac{{10}}{9}Hz\)
\( \Rightarrow \omega = 2\pi f = \dfrac{{20\pi }}{9}\left( {rad/s} \right)\)
+ Phương trình sóng tại N: \({u_N} = 4cos\left( {\dfrac{{20\pi }}{9}t - \dfrac{\pi }{2} - \dfrac{{2\pi .ON}}{\lambda }} \right) = 4\cos \left( {\dfrac{{20\pi }}{9}t - \dfrac{{5\pi }}{9}} \right)cm\)
Ở mặt chất lỏng, tại hai điểm \({S_1}\) và \({S_2}\) cách nhau 28 cm có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra sóng kết hợp. Gọi \({\Delta _1}\) và \({\Delta _2}\) là hai đường thẳng ở mặt chất lỏng cùng vuông góc với đoạn thẳng \({S_1}\) \({S_2}\) và cách nhau 9 cm. Biết số điểm cục đại giao thoa trên \({\Delta _1}\)và \({\Delta _2}\) tương ứng là 7 và 3. Số điểm cực đại giao thoa trên đoạn thẳng \({S_1}{S_2}\) là
Ta có hình vẽ:
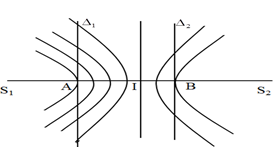
Từ hình vẽ ta thấy, để trên \({\Delta _1}\) có 7 cực đại, tại điểm A là cực đại bậc 4 \( \Rightarrow IA = 4\dfrac{\lambda }{2} = 2\lambda \)
Trên \({\Delta _2}\) có 3 cực đại, tại điểm B là cực đại bậc 2 \( \Rightarrow IB = 2\dfrac{\lambda }{2} = \lambda \)
Khoảng cách giữa \({\Delta _1}\) và \({\Delta _2}\) là:
\(AB = 3\lambda = 9\left( {cm} \right) \Rightarrow \lambda = 3\left( {cm} \right)\)
Số điểm cực đại trên đoạn \({S_1}{S_2}\) là: \(n = 2\left[ {\dfrac{{{S_1}{S_2}}}{\lambda }} \right] + 1 = 2.\left[ {\dfrac{{28}}{3}} \right] + 1 = 19\) (cực đại)
Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng 6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhật, AD = 30cm. Số điểm cực đại và đứng yên trên đoạn CD lần lượt là
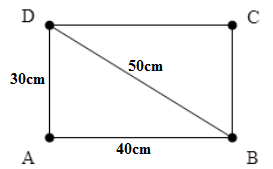
Áp dụng định lí Pitago ta có: \(DB = CA = 50cm\)
+ Số điểm cực đại giao thoa trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } \le k \le \dfrac{{DB - DA}}{\lambda } \Leftrightarrow \dfrac{{30 - 50}}{6} \le k \le \dfrac{{50 - 30}}{6}\\ \Leftrightarrow - 3,3 \le k \le 3,3 \Rightarrow k = - 3; - 2;...;3\end{array}\)
Có 7 giá trị của k nguyên thoả mãn nên có 7 cực đại giao thoa
+ Số điểm đứng yên trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } - \dfrac{1}{2} \le k \le \dfrac{{DB - DA}}{\lambda } - \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{30 - 50}}{6} - \dfrac{1}{2} \le k \le \dfrac{{50 - 30}}{6} - \dfrac{1}{2}\\ \Leftrightarrow - 3,8 \le k \le 2,8 \Rightarrow k = - 3; - 2;...;2\end{array}\)
Có 6 giá trị của k nguyên thoả mãn nên có 6 điểm đứng yên.
Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp A và B dao động cùng pha với tần số \(20 Hz.\) Người ta thấy điểm M dao động cực đại và giữa M với đường trung trực của AB có một đường không dao động. Điểm M thuộc cực đại ứng với
Ta có hình ảnh giao thoa sóng:
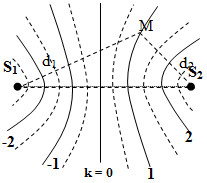
Giữa \(M\) và đường trung trực của \(AB\) có một đường không dao động
\( \Rightarrow \) Điểm \(M\) thuộc cực đại ứng với \(k = 1.\)
Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li dộ dao động của phần tử tại M là 3cm thì li độ dao động của phần tử tại N là -3cm. Biên độ dao động sóng bằng
Độ lệch pha của hai phần tử\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi \dfrac{\lambda }{3}}}{\lambda } = \dfrac{{2\pi }}{3}\)
Vẽ trên vòng tròn lượng giác, ta có:
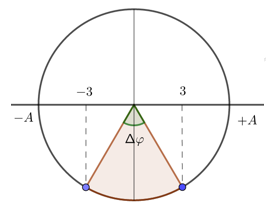
Từ vòng tròn lượng giác, ta có: \(\sin \dfrac{{\Delta \varphi }}{2} = \dfrac{3}{A} \Rightarrow A = \dfrac{3}{{\sin \dfrac{{\Delta \varphi }}{2}}} = \dfrac{3}{{\sin \dfrac{\pi }{3}}} = 2\sqrt 3 cm\)

