Ở mặt chất lỏng, tại hai điểm \({S_1}\) và \({S_2}\) cách nhau 28 cm có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra sóng kết hợp. Gọi \({\Delta _1}\) và \({\Delta _2}\) là hai đường thẳng ở mặt chất lỏng cùng vuông góc với đoạn thẳng \({S_1}\) \({S_2}\) và cách nhau 9 cm. Biết số điểm cục đại giao thoa trên \({\Delta _1}\)và \({\Delta _2}\) tương ứng là 7 và 3. Số điểm cực đại giao thoa trên đoạn thẳng \({S_1}{S_2}\) là
Trả lời bởi giáo viên
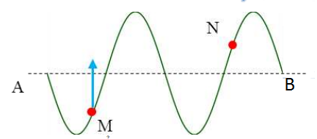
Ta có hình vẽ:
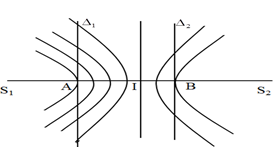
Từ hình vẽ ta thấy, để trên \({\Delta _1}\) có 7 cực đại, tại điểm A là cực đại bậc 4 \( \Rightarrow IA = 4\dfrac{\lambda }{2} = 2\lambda \)
Trên \({\Delta _2}\) có 3 cực đại, tại điểm B là cực đại bậc 2 \( \Rightarrow IB = 2\dfrac{\lambda }{2} = \lambda \)
Khoảng cách giữa \({\Delta _1}\) và \({\Delta _2}\) là:
\(AB = 3\lambda = 9\left( {cm} \right) \Rightarrow \lambda = 3\left( {cm} \right)\)
Số điểm cực đại trên đoạn \({S_1}{S_2}\) là: \(n = 2\left[ {\dfrac{{{S_1}{S_2}}}{\lambda }} \right] + 1 = 2.\left[ {\dfrac{{28}}{3}} \right] + 1 = 19\) (cực đại)
Hướng dẫn giải:
Khoảng cách giữa hai cực đại liên tiếp trên đường nối hai nguồn: \(\dfrac{\lambda }{2}\)
Số cực đại trên đường nối hai nguồn: \(n = 2\left[ {\dfrac{{{S_1}{S_2}}}{\lambda }} \right] + 1\)