Các loại dao động

Ta có:

+ Tần số dao động riêng của con lắc:

\(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}}  = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{100}}{{0,1}}}  = 5H{\rm{z}}\)

+  f₀ < f_2­ < f₁

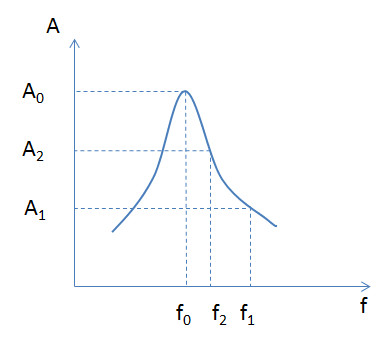
Từ đồ thị ta suy ra: A₂ > A₁

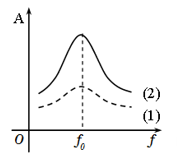
A - sai vì: Biên độ dao động cưỡng bức của hệ cơ học khi xảy ra hiện tượng cộng hưởng có phụ thuộc vào lực cản của môi trường

Ta có:

\(\frac{{A - {A_3}}}{A} = 10\%  = 0,1 \to \frac{{{A_3}}}{A} = 0,9\)

Mặt khác, ta có:

\({\rm{W}} = \frac{1}{2}k{A^2}\)

\( \to \frac{{{{\rm{W}}_3}}}{{\rm{W}}} = \frac{{A_3^2}}{{{A^2}}} = 0,{9^2} = 0,81 = 81\% \)

=> Phần trăm cơ năng còn lại sau khoảng thời gian đó là 81%

Ta có, độ giảm biên độ sau mỗi chu kì là:

\(\Delta A = \frac{{4\mu mg}}{k}\)

=> Độ giảm biên độ mỗi lần vật qua VTCB là:

\(\frac{{\Delta A}}{2} = \frac{{\frac{{4\mu mg}}{k}}}{2} = \frac{{2\mu mg}}{k} = \frac{{2.0,01.0,1.10}}{{100}} = {2.10^{ - 4}}m = 0,2mm\)

Thời gian từ lúc vật dao động đến khi dừng lại là:

\(\Delta t = N.T = \frac{{AkT}}{{4\mu mg}} = \frac{{Ak2\pi \sqrt {\frac{m}{k}} }}{{4\mu mg}} = \frac{{A.2\pi \sqrt k }}{{4\mu g\sqrt m }} = \frac{{0,1.2\pi \sqrt {100} }}{{4.0,1.10\sqrt {0,1} }} = 5{\rm{s}}\)

Ban đầu biên độ dao động của vật là A

Sau 1 dao động toàn phần biên độ dao động của vật là:

\({A_1} = A - 0,02A = 0,98A\)

Sau 2 dao động toàn phần biên độ dao động của vật là:

\({A_2} = {A_1} - 0,02{A_1} = 0,98A - 0,02.0,98A = 0,9604A\)

Phần trăm cơ năng mất đi sau 2 dao động toàn phần liên tiếp là:

\(\begin{array}{l}\Delta {\rm{W}} = \dfrac{{{\rm{W}} - {{\rm{W}}_2}}}{{\rm{W}}}.100\%  = \dfrac{{{A^2} - A_2^2}}{{{A^2}}}.100\% \\ \Rightarrow \Delta {\rm{W}} = \dfrac{{{A^2} - 0,{{9604}^2}.{A^2}}}{{{A^2}}}.100\%  = 7,8\% \end{array}\)

Hiện tượng cộng hưởng xảy ra khi:

\(\omega  = {\omega _0} = 10\pi  \Rightarrow f = \dfrac{{10\pi }}{{2\pi }} = 5\left( {Hz} \right)\)

Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động duy trì.