Định luật khúc xạ ánh sáng

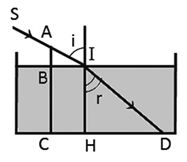
Theo đầu bài, ta có:

\(\left\{ \begin{array}{l}{n_1} = 1\\{n_2} = \frac{4}{3}\end{array} \right.;C{\rm{D}} = 190cm;BI = CH = 40cm;AB = 30cm\)

Từ hình vẽ, ta có:

\(\begin{array}{l}\tan i = \frac{{BI}}{{AB}} = \frac{{40}}{{30}} = \frac{4}{3} \to i = 53,{1^0}\\\end{array}\)

Theo định luật khúc xạ ánh sáng, ta có:

\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \to {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{1.\sin 53,1}}{{\frac{4}{3}}} = 0,6 \to r = 36,{87^0}\)

Mặt khác, từ hình ta có: \({\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HD}}{{IH}} = \frac{{C{\rm{D}} - CH}}{{IH}} \to IH = \frac{{C{\rm{D}} - CH}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{190 - 40}}{{0,75}} = 200cm\)

Ta có, ánh nắng chiếu nghiêng một góc 30⁰ so với phương ngang => i = 60⁰

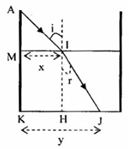
Từ hình vẽ ta có:

\(\tan i = \frac{x}{{MA}} \to x = MAtan60 = 20\sqrt 3 cm\)

\({\mathop{\rm s}\nolimits} {\rm{inr}} = \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}\)

+ Theo định luật khúc xạ ánh sáng, ta có:

\(\begin{array}{l}\frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n \leftrightarrow \frac{{\sin {{60}^0}}}{{\frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }}}} = \frac{4}{3} \to \frac{{HJ}}{{\sqrt {H{I^2} + H{J^2}} }} = \frac{{3\sqrt 3 }}{8}\\ \leftrightarrow \frac{{H{J^2}}}{{H{I^2} + H{J^2}}} = \frac{{27}}{{64}} \to H{J^2} = \frac{{27}}{{37}}H{I^2} \to HJ = \sqrt {\frac{{27}}{{37}}} .60 = 51,25cm\end{array}\)

Vậy vệt sáng ở dưới đáy bể là: \(y = x + HJ = 20\sqrt 3  + 51,25 = 85,9cm\)

Ta có: chiết suất tuyệt đối của kim cương:

\(n = \frac{c}{v} \to v = \frac{c}{n} = \frac{{{{3.10}^8}}}{{2,42}} = 1,{24.10^8}m/s = 124000km/s\)

Áp dụng định luật phản xạ ánh sáng, tia phản xạ và tia khúc xạ vuông góc với nhau ta có:

 r + i’ = 90° hay là r + i = 90°.

Ta có tốc độ ánh sáng trong không khí lớn hơn tốc độ ánh sáng trong nước: \({v_1} > {v_2}\,\,\,\left( 1 \right)\)

Tia sáng truyền từ nước ra ngoài không khí. Áp dụng định luật khúc xạ ánh sáng ta có:

\(n\sin i = \sin \,r \Rightarrow i < r\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có: \({v_1} > {v_2};i < r\)

Hướng dẫn giải:

Theo định luật khúc xạ ánh sáng, ta có:

\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)

Theo đề bài: \(i{\rm{ }} = {\rm{ }}2r\)

\(1\sin i = 1,5{\mathop{\rm s}\nolimits} {\rm{in}}\frac{i}{2} \leftrightarrow 2\sin \frac{i}{2}{\rm{cos}}\frac{i}{2} = 1,5.\sin \frac{i}{2}\)       (1)

Do \(i{\rm{ }} = {\rm{ }}2r\) nên \(i \ne 0\)

\( \to (1) \leftrightarrow 2c{\rm{os}}\frac{i}{2} = 1,5 \to c{\rm{os}}\frac{i}{2} = \frac{3}{4} \to \frac{i}{2} = 41,{4^0} \to i = 82,{8^0}\)

Tia khúc xạ vuông góc với tia phản xạ, ta có hình vẽ:

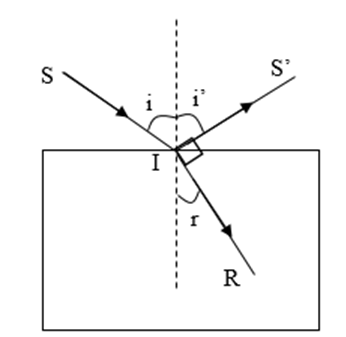
Ta có góc phản xạ: \(i' = i\)

Tia tới và tia phản xạ vuông góc, ta có:

\(i' + r = {90^0} \Rightarrow \sin r = \cos i' = \cos i\)

Áp dụng công thức định luật khúc xạ ánh sáng, ta có:

\(\sin i = n\sin r \Rightarrow n = \dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin i}}{{\cos i}} = \tan i\)

+ Tia khúc xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến → A đúng

+ Tia khúc xạ nằm ở môi trường thứ 2 tiếp giáp với môi trường chứa tia tới → B đúng

+ Góc khúc xạ có thể lớn hơn, nhỏ hơn hoặc bằng góc tới (góc khúc xạ bằng góc tới khi góc khúc xạ bằng 0) → C đúng, D sai

Ta có hình vẽ:

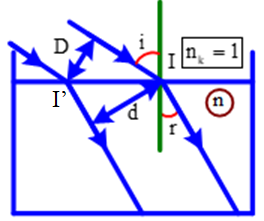
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:

\(\sin i = n\sin r \Rightarrow \sin r = \dfrac{{\sin i}}{n} = \dfrac{{\sin {{45}^0}}}{{1,5}} \Rightarrow r \approx 28,{13^0}\)

Từ hình vẽ ta thấy: \(II' = \dfrac{D}{{\cos i}} = \dfrac{d}{{\cos r}} \Rightarrow d = D\dfrac{{\cos r}}{{\cos i}}\)

\( \Rightarrow d = 10.\dfrac{{\cos {{28}^0}}}{{\cos {{45}^0}}} \approx 12,47\,\,\left( {mm} \right)\)

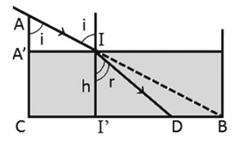
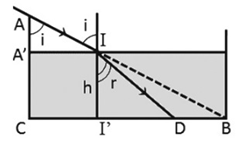
Từ hình vẽ ta thấy: \(\sin i = \frac{{A'I}}{{AI}} = \frac{{CB}}{{AB}} = \frac{{40}}{{\sqrt {{{30}^2} + {{40}^2}} }} = 0,8\)

\( \Rightarrow \frac{1}{{{{\sin }^2}i}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \frac{1}{{0,{8^2}}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \tan i = \frac{4}{3}\)

Áp dụng công thức định luật khúc xạ ánh sáng, ta có:

\(\sin i = n\sin r \Rightarrow \sin r = \frac{{\sin i}}{n} = \frac{{0,8}}{{\frac{4}{3}}} = 0,6\)

\( \Rightarrow \frac{1}{{{{\sin }^2}r}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \frac{1}{{0,{6^2}}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \tan r = 0,75\)

Lại có: \(h = II' = \frac{2}{3}AC = \frac{2}{3}.30 = 20{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)

Ta có:

\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{I'B = h.\tan i}\\{I'D = h.\tan r}\end{array}} \right. \Rightarrow d = I'B - I'D = h\left( {\tan i - \tan r} \right)}\\{ \Rightarrow d = 20.\left( {\frac{4}{3} - 0,75} \right) \approx 11,7{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)

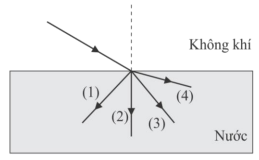
Ta có: \({n_1} < {n_2}\)

\({n_1}\sin i = {n_2}\sin r\) \(\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}} > 1\)

\( \Rightarrow i > r\)

Mặt khác: Theo định luật khúc xạ ánh sáng thì:

+ Tia khúc xạ nằm trong mặt phẳng tới

+ Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới.

Vậy đường kẻ vẽ đúng đường truyền của tia sáng đơn sắc trong trường hợp đang xét là đường (3).