Dòng điện trong kim loại
Kỳ thi ĐGNL ĐHQG Hà Nội
Một bóng đèn \(220V - 40W\) có dây tóc làm bằng vônfram. Điện trở của dây tóc bóng đèn ở \({20^0}C\) là \({R_0} = 121\Omega \) . Nhiệt độ của dây tóc bóng khi bóng đèn sáng bình thường là bao nhiêu? Biết hệ số nhiệt điện trở của vônfram là \(\alpha = {\rm{ }}{4,5.10^{ - 3}}{K^{ - 1}}\).
Ta có:
+ Khi thắp sáng, đèn sáng bình thường, điện trở của bóng đèn là:
\({R_S} = \dfrac{{{U^2}}}{P} = \dfrac{{{{220}^2}}}{{40}} = 1210\Omega \)
Mặt khác:
\(\begin{array}{l}{R_s} = {R_0}{\rm{[}}1 + \alpha (t - {t_0}){\rm{]}} \leftrightarrow 1210 = 121[1 + 4,{5.10^{ - 3}}(t - 20){\rm{]}}\\ \to t = {2020^0}C\end{array}\)
Dây tóc của bóng đèn 220V - 200W khi sáng bình thường ở nhiệt độ 25000C có điện trở gấp 10,8 lần so với điện trở ở 1000C. Hệ số nhiệt điện trở α của dây tóc là?
Ta có:
+ Khi thắp sáng, đèn sáng bình thường ở nhiệt độ 25000C điện trở của bóng đèn là:
\({R_S} = \frac{{{U^2}}}{P} = \frac{{{{220}^2}}}{{200}} = 242\Omega \)
+ Ở nhiệt độ 1000C : \({R_0} = \frac{{{R_S}}}{{{\rm{[}}1 + \alpha (100 - {t_0}){\rm{]}}}} = \frac{{242}}{{10,8}} = 22,4\Omega \)
Ta có:
\(\begin{array}{l}{R_S} = {R_0}{\rm{[}}1 + \alpha (2500 - 100){\rm{]}}\\ \to \alpha = 4,{08.10^{ - 3}}{K^{ - 1}}\end{array}\)
Ở nhiệt độ t1 = 250C , hiệu điện thế giữa hai cực của bóng đèn là U1 = 20mV thì cường độ dòng điện qua đèn là I1 = 8mA. Khi sáng bình thường, hiệu điện thế giữa hai cực của bóng đèn là U2 = 240V thì cường độ dòng điện chạy qua đèn là I2 = 8A. Nhiệt độ của dây tóc bóng đèn khi đèn sáng bình thường là? Biết hệ số nhiệt điện trở của dây tóc làm bóng đèn là α = 4,2.10-3K-1
Ta có:
+ Điện trở của dây tóc ở 250C: \({R_1} = \frac{{{U_1}}}{{{I_1}}} = \frac{{{{20.10}^{ - 3}}}}{{{{8.10}^{ - 3}}}} = 2,5\Omega \)
+ Điện trở của dây tóc khi sáng bình thường: \({R_2} = \frac{{{U_2}}}{{{I_2}}} = \frac{{240}}{8} = 30\Omega \)
Mặt khác:
\(\begin{array}{l}{R_2} = {R_1}{\rm{[}}1 + \alpha ({t_2} - {t_1}){\rm{]}} \leftrightarrow {\rm{30 = 2,5[1 + 4,2}}{\rm{.1}}{{\rm{0}}^{ - 3}}({t_2} - 25)\\ \to {t_2} = 2644,{05^0}C\end{array}\)
Một mối hàn của cặp nhiệt điện nhúng vào nước đá đang tan, mối hàn kia được nhúng vào hơi nước sôi. Dùng milivôn kế đo được suất điện động của cặp nhiệt điện là 4,25mV. Hệ số nhiệt điện động của cặp nhiệt điện đó?
+ Nhiệt độ của nước đá đang tan là t1 = 00C
+ Nhiệt độ của hơi nước sôi là t2 = 1000C
\(E = {\alpha _T}({T_2} - {T_1}) \to {\alpha _T} = \frac{E}{{{T_2} - {T_1}}} = \frac{{4,{{25.10}^{ - 3}}}}{{100}} = 42,{5.10^{ - 6}}V/K\)
Nhiệt kế điện thực chất là một cặp nhiệt điện dùng để đo nhiệt độ rất cao hoặc rất thấp mà ta không thể dùng nhiệt kế thông thường để đo được. Dùng nhiệt kế điện có hệ số nhiệt điện động αT = 42μ V/K để đo nhiệt độ của một lò nung với một mối hàn đặt trong không khí ở 200C còn mối hàn kia đặt vào lò xo thì mấy milivôn kế chỉ 50,2mV. Nhiệt độ của lò nung là?
Ta có:
\(E = {\alpha _T}({T_2} - {T_1}) \to {T_2} = \frac{E}{{{\alpha _T}}} + {T_1} = \frac{{{{50,2.10}^{ - 3}}}}{{{{42.10}^{ - 6}}}} + 20 = 1215,2\)
Ta suy ra nhiệt độ của lò nung là: \(t = {1215,2^0}C\)
Để xác định điện trở của một vật dẫn kim loại, một học sinh mắc nối tiếp điện trở này với một ampe kế. Đặt vào hai đầu đoạn mạch trên một biến thế nguồn (nguồn điện có hiệu điện thế thay đổi được). Thay đổi giá trị của biến thế nguồn, đọc giá trị dòng điện của ampe kế, số liệu thu được được thể hiện bằng đồ thị như hình vẽ. Điện trở vật dẫn gần nhất giá trị nào sau đây:
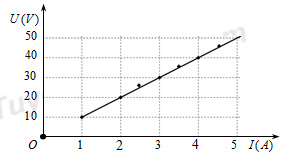
Từ đồ thị ta thấy, khi \(U = 20V\) thì \(I = 2A\)
Suy ra: \(R = \dfrac{U}{I} = \dfrac{{20}}{2} = 10\Omega \)
Cặp nhiệt điện sắt - constantan có hệ số nhiệt điện động là 52 μV/K và điện trở trong r = 0,5 Ω. Nối cặp nhiệt điện này với điện kế G có điện trở trong là 20 Ω. Đặt một mối hàn của cặp nhiệt điện này trong không khí ở 20oC và nhúng mối hàn thứ hai vào trong lò điện có nhiệt độ 6200C. Xác định cường độ dòng điện chạy qua điện kế G.
Suất điện động nhiệt điện của cặp nhiệt điện sắt - constantan :
\(\xi = {\alpha _T}.\left( {{T_1} - {T_2}} \right) = {52.10^{ - 6}}.\left( {620 - 20} \right) = 31,2mV\)
Áp dụng định luật Ôm đối với mạch điện kín, ta tính được cường độ dòng điện chạy qua điện kế G là:
\(I = \dfrac{\xi }{{R + r}} = \dfrac{{31,2}}{{20 + 0,5}} \approx 1,52mA\)
Một bóng đèn 220V - 100W khi sáng bình thường thì nhiệt độ của dây tóc đèn là 20000C . Xác định điện trở của đèn khi thắp sáng và khi không thắp sáng, biết rằng nhiệt độ môi trường là 200C và dây tóc đèn làm bằng vonfram, biết hệ số nhiệt điện trở của vonfram là \(\alpha = 4,{5.10^{ - 3}}\,\,\left( {{K^{ - 1}}} \right)\)
Điện trở của bóng đèn khi sáng bình thường (ở t = 20000C) là:
\(R = \dfrac{{{U^2}}}{P} = \dfrac{{{{220}^2}}}{{100}} = 484\Omega \)
Mặt khác ta có: R = R0.(1 + α.(t – t0))
→ Điện trở bóng đèn khi không thắp sáng (ở t0 = 200C) là:
\({R_0} = \dfrac{R}{{1 + \alpha \left( {t - {t_0}} \right)}} = \dfrac{{484}}{{1 + 4,{{5.10}^{ - 3}}.\left( {2000 - 20} \right)}} = 48,84\Omega \)
Một dây bạch kim ở 200C có điện trở suất 10,6.10-8 Ω.m. Biết điện trở suất của bạch kim trong khoảng nhiệt độ từ 00 đến 20000C tăng bậc nhất theo nhiệt độ với hệ số nhiệt điện trở không đổi bằng 3,9.10-3K-1. Điện trở suất của dây bạch kim này ở 16800C là
Điện trở suất của dây bạch kim này ở 16800C là:
\(\rho = {\rho _0}.\left( {1 + \alpha \left( {t - {t_0}} \right)} \right) = 10,{6.10^{ - 8}}.\left( {1 + 3,{{9.10}^{ - 3}}.\left( {1680 - 20} \right)} \right) = 79,{2.10^{ - 8}}\Omega m\)

