Mạch R, L, C mắc nối tiếp
Kỳ thi ĐGNL ĐHQG Hà Nội
Trong mạch R, L, C nối tiếp với điện áp hai đầu đoạn mạch là u và cường độ dòng điện qua mạch là i. Chọn phát biểu đúng:
A - sai vì ZL > ZC ta chỉ có thể kểt luận là u sớm pha hơn i
B- sai vì ZL < ZC ta chỉ có thể kết luận là u chậm pha hơn i
C - sai vì R = 0 thì u và i không thể cùng pha
D- đúng
Đặt điện áp \(u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)\) vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\)
Ta có:
+ uL nhanh pha hơn i một góc \(\dfrac{\pi }{2}\)
+ Cường độ dòng điện cực đại:
\({I_0} = \dfrac{{{U_0}}}{{{Z_L}}} = \dfrac{{{U_0}}}{{\omega L}}\)
=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là:
\(i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)\)
Đồ thị cường độ dòng điện như hình vẽ
Cường độ dòng điện tức thời có biểu thức
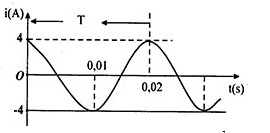
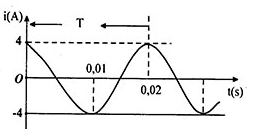
Từ đồ thị ta có:
+ Chu kì:
\(T = 0,02{\rm{s}} \to \omega {\rm{ = }}\frac{{2\pi }}{T} = 100\pi (ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại:
\({I_0} = 4(A)\)
+ Tại t = 0:
\(i = 4 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 4}} \to c{\rm{os}}\varphi {\rm{ = 1}} \to \varphi {\rm{ = 0}}\)
=> Biểu thức cường độ dòng điện tức thời:
\(i = 4c{\rm{os}}\left( {100\pi t} \right)A\)
Một mạch điện xoay chiều nối tiếp có \(R = 60\Omega ;L = \dfrac{{0,2}}{\pi }H;C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\) mắc vào mạng điện xoay chiều có chu kì $0,02 s$. Tổng trở của đoạn mạch là:
Ta có:
\(\begin{array}{l}\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,02}} = 100\pi (ra{\rm{d/s)}}\\R = 60\Omega \\{Z_L} = \omega L = 100\pi \dfrac{{0,2}}{\pi } = 20\Omega \\{Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi \dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \end{array}\)
Tổng trở của mạch:
\(Z = \sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{60}^2} + {{\left( {20 - 100} \right)}^2}} = 100\Omega \)
Mạch nối tiếp gồm ampe kế, \(C = 63,6\mu F,L = 0,318H\) rồi mắc vào mạng điện xoay chiều $(220V – 50 Hz)$. Số chỉ ampe kế là:
Ta có:
+ Hiệu điện thế hiệu dụng: \(U = 220V\)
+ Cảm kháng:
\({Z_L} = \omega L = 2\pi fL = 2\pi .50.0,318 = 100\Omega \)
+ Dung kháng:
\({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi {{.50.63,6.10}^{ - 6}}}} = 50\Omega \)
+ Tổng trở của mạch: \(Z = \left| {{Z_L} - {Z_C}} \right| = 50\Omega \)
Số chỉ ampe kế chính là cường độ dòng điện hiệu dụng:
\(I = \dfrac{U}{Z} = \dfrac{{220}}{{50}} = 4,4(A)\)
Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng \(Z_L=50\Omega\) như hình sau:
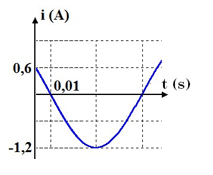
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm.
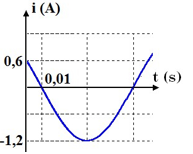
Từ đồ thị ta có:
\(\dfrac{T}{{12}} = 0,01{\rm{s}} \to T = 0,12{\rm{s}} \\\to \omega {\rm{ = }}\dfrac{{2\pi }}{T} = \dfrac{{50\pi }}{3}(ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại:
\({I_0} = 1,2(A)\)
+ Tại \(t = 0\): \(i = 0,6A\) và đang giảm:
\(i = 0,6 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 0}}{\rm{,6}} \\\to c{\rm{os}}\varphi {\rm{ = }}\dfrac{{0,6}}{{1,2}} = \dfrac{1}{2} \to \varphi {\rm{ = }}\dfrac{\pi }{3}\)
=> Biểu thức cường độ dòng điện tức thời:
\(i = 1,2c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3}} \right)A\)
+ Ta có uL nhanh pha hơn i một góc \(\dfrac{\pi }{2}\)
+ Hiệu điện thế cực đại:
\({U_0} = {I_0}.{Z_L} = 1,2.50 = 60(V)\)
=> Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
$u = 60c{\rm{os}}\left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{\pi }{3} + \dfrac{\pi }{2} + \dfrac{\pi }{2}} \right) \\= 60\sin \left( {\dfrac{{50\pi }}{3}t + \dfrac{{4\pi }}{3}} \right)V$
Đặt điện áp \(u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t{\rm{ }}-\pi /3){\rm{ }}V\) vào hai đầu một tụ điện có điện dung \(\frac{{{{2.10}^{ - 4}}}}{\pi }{\rm{ }}F\) . Ở thời điểm điện áp giữa hai đầu tụ điện là 150 V thì cường độ dòng điện trong mạch là 4A. Biểu thức của cường độ dòng điện trong mạch là:
Do mạch chỉ có C nên:
\(u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Lại có:
\({U_0} = {I_0}{Z_C}\)
\( \to \frac{{{{150}^2}}}{{{{(50.{I_0})}^2}}} + \frac{{{4^2}}}{{I_0^2}} = 1 \to {I_0} = 5(A)\)
Ta có i sớm pha hơn uC một góc: \(\frac{\pi }{2}\)
$ \to {\varphi _i} = \frac{\pi }{2} + \left( { - \frac{\pi }{3}} \right) = \frac{\pi }{6}$
\( \to i{\rm{ }} = {\rm{ }}5cos(100\pi t{\rm{ }} + \frac{\pi }{6}){\rm{ }}A\)
Đặt điện áp xoay chiều \(u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t{\rm{ }}-\pi /3){\rm{ }}V\) vào hai đầu một cuộn cảm thuần có độ tự cảm \(\frac{1}{{2\pi }}{\rm{ }}H\) . Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt 2 {\rm{ }}V\) thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là
Do mạch chỉ có cuộn dây nên:
\(u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Ta có: \({Z_L} = {\text{ }}\omega L{\text{ }} = {\text{ }}50\Omega \to {U_0} = {\text{ }}50{\text{ }}{I_0}\)
\( \to \frac{{{{(100\sqrt 2 )}^2}}}{{{{(50{I_0})}^2}}} + \frac{{{2^2}}}{{I_0^2}} = 1 \to {I_0} = 2\sqrt 3 (A)\)
Mạch có cuộn dây nên i chậm pha hơn u góc \(\frac{\pi }{2}{\text{ }}\)
\(\to {\varphi _{i}} = - 5\pi /6\)
$ \to i = 2\sqrt 3 {\rm{cos(100}}\pi {\rm{t - }}\frac{{5\pi }}{6})(A)$
Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 450. Chọn kết luận đúng:
Ta có :
+ u nhanh pha hơn i một góc 450
+ độ lệch pha giữa u và i được xác định bởi biểu thức :
\(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
\(\begin{array}{l} \to \tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \tan \dfrac{\pi }{4}\\ \to {Z_L} - {Z_C} = R\end{array}\)
Mạch điện xoay chiều RLC nối tiếp. Biết điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời là: 600 và\(R = 10\sqrt 3 \Omega ;{Z_L} = 50\Omega \). Dung kháng của tụ điện có giá trị là
Ta có, điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời góc 600
\( \to \varphi = - \dfrac{\pi }{3}\)
Mặt khác, ta có:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \tan ( - \dfrac{\pi }{3}) \to {Z_L} - {Z_C} = - \sqrt 3 R\\ \to {Z_C} = {Z_L} + \sqrt 3 R = 50 + \sqrt 3 .10\sqrt 3 = 80\Omega \end{array}\)
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Hiệu điện thế hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Hệ số công suất \(cosφ\) của đoạn mạch là:
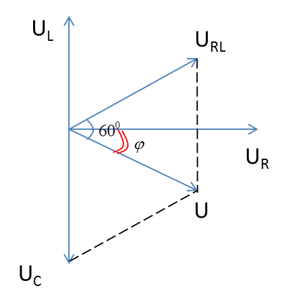
Từ giản đồ véc tơ, ta có:
\(\varphi = \pi - \left( {\dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) = \dfrac{\pi }{6} \to c{\rm{os}}\varphi = c{\rm{os}}\dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{2}\)
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 3 lần dung kháng của tụ điện. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu tụ điện có giá trị tương ứng là \(60V\) và \(20V\). Khi đó, điện áp tức thời giữa hai đầu đoạn mạch là
Ta có: \({Z_L} = 3{Z_C} \Rightarrow {u_L} = - 3{u_C}\) (do \({u_L}\) ngược pha với \({u_C}\))
Tại thời điểm t: \(\left\{ \begin{array}{l}{u_R} = 60V\\{u_C} = 20V\\{u_L} = - 3{u_C} = - 60V\end{array} \right.\)
Điện áp tức thời giữa hai đầu đoạn mạch khi đó: \(u = {u_R} + {u_L} + {u_C} = 60 + \left( { - 60} \right) + 20 = 20V\)
Trong đoạn mạch điện xoay chiều RLC nối tiếp, nếu điện áp hiệu dụng giữa hai bản tu gấp hai lần điện áp điện áp hiệu dụng giữa hai đầu cuộn dây thuần cảm thì điện áp giữa hai đầu đoạn mạch sẽ
Ta có giản đồ vecto trong trường hợp: UC = 2.UL:
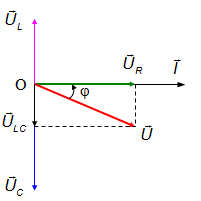
Vậy u trễ pha với i.
Đặt điện áp \(u = 100\cos \left( {100\pi t + \frac{\pi }{3}} \right)\,\,\left( V \right)\) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện qua mạch có biểu thức \(i = 2\cos \left( {100\pi t - \frac{\pi }{6}} \right)\,\,\left( A \right)\). Độ lệch pha giữa điện áp và cường độ dòng điện là
Độ lệch pha giữa điện áp và cường độ dòng điện là:
\(\Delta \varphi = {\varphi _u} - {\varphi _i} = \frac{\pi }{3} - \left( { - \frac{\pi }{6}} \right) = \frac{\pi }{2}\,\,\left( {rad} \right)\)
Đề thi THPT QG - 2020
Đặt điện áp xoay chiều \(u{\rm{ }} = U\sqrt 2 cos100\pi t\) (t tính bằng s) vào hai đầu đoạn mạch R, L, C mắc nối tiếp thì có cộng hưởng điện. Biết cuộn cảm có cảm kháng \(30\Omega \). Điện dung của tụ điện có giá trị là
+ Từ phương trình điện áp, ta có \(\omega = 100\pi \left( {rad/s} \right)\)
+ Mạch có cộng hưởng điện \( \Rightarrow {Z_L} = {Z_C} = 30\Omega \)
+ Lại có, dung kháng: \({Z_C} = \frac{1}{{\omega C}} \Rightarrow C = \frac{1}{{\omega .{Z_C}}} = \frac{1}{{100\pi .30}} = 1,{061.10^{ - 4}}F\)
Đề thi THPT QG - 2020
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở \(120\Omega \) mắc nối tiếp với tụ điện. Biết dung kháng của tụ điện là \(50\Omega \). Tổng trở của đoạn mạch là
Ta có, mạch gồm R nt tụ điện, tổng trở của mạch: \(Z = \sqrt {{R^2} + Z_C^2} = \sqrt {{{120}^2} + {{50}^2}} = 130\Omega \)

