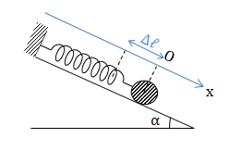
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt - π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t = 0, lực đàn hồi đổi chiều lần đầu tại thời điểm:
Trả lời bởi giáo viên
Từ phương trình dao động, ta có chu kì dao động: \(T = \dfrac{{2\pi }}{\omega } = 1{\rm{s}}\)
Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = 5c{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = 2,5cm\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
Lực đàn hồi đổi chiều tại vị trí cân bằng
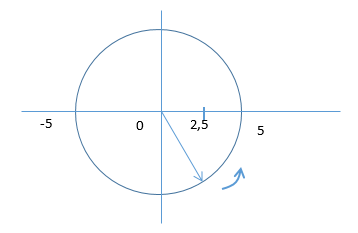
Từ vòng tròn lượng giác,
=> Lực đàn hồi đổi chiều lần đầu kể từ t = 0 tại thời điểm: \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}} = \dfrac{5}{{12}}s\)
Hướng dẫn giải:
+ Xác định vị trí tại thời điểm t = 0: \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi \\v = - A\omega \sin \varphi \end{array} \right.\)
+ Xác định vị trí lực đàn hồi đổi chiều
+ Sử dụng vòng tròn lượng giác và trục thời gian suy ra từ vòng tròn