Phép nhân số nguyên, phép chia hết, bội và ước của một số nguyên
Sách kết nối tri thức với cuộc sống
Có bao nhiêu số nguyên \(x\) biết: \(x\; \vdots \;7\) và \(\left| x \right| < 45?\)
\(B\left( 7 \right) = \left\{ {0; \pm 7; \pm 14; \pm 21; \pm 28; \pm 35; \pm 42; \pm 49...} \right\}\)
Vậy các số nguyên \(x\) cần tìm là: \(\left\{ {0; \pm 7; \pm 14; \pm 21; \pm 28; \pm 35; \pm 42} \right\}\)
Có tất cả \(13\) số nguyên cần tìm.
Giá trị lớn nhất của \(a\) thỏa mãn \(a - 5\) là ước của \( - 8\) là:
\(a - 5\) là ước của \( - 8\)
\( \Rightarrow \;\left( {a - 5} \right) \in U\left( { - 8} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\;\)
Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 13\).
Tìm \(x\) biết: \(\left( { - 8} \right).x = 160\).
\( - 8.x = 160\)
\(x = 160:(-8)\)
\(x = - 20\)
Cho \(x \in \mathbb{Z}\) và \(\left( { - 215 + x} \right) \vdots \,6\) thì:
Ta có:
\(\left( { - 215 + x} \right) \vdots \,6\)
\(\left( { - 216 + 1 + x} \right) \vdots \,6\)
\(\left( {x + 1} \right) \vdots 6\) (do\( - 216 \vdots 6\))
Do đó \(x + 1 = 6k \Rightarrow x = 6k - 1\)
Vậy \(x\) chia cho \(6\) dư \( 5\).
Tìm tất cả các ước chung của \(25\) và \( - 40.\)
Ta có:
\(U\left( {25} \right) = \left\{ { \pm 1; \pm 5; \pm 25} \right\}\)
\(U\left( { - 40} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 5; \pm 8; \pm 10; \pm 20; \pm 40} \right\}\)
Vậy \(UC\left( {25; - 40} \right) = \left\{ { \pm 1; \pm 5} \right\}\)
Giá trị nào dưới đây của \(x\) thỏa mãn \( - 24.\left( {x - 5} \right) = - 192?\)
\(\begin{array}{l} - 24\left( {x - 5} \right) = - 192\\x - 5 = ( - 192):( - 24)\\x - 5 = 8\\x = 8 + 5\\x = 13\end{array}\).
Tìm \(n \in Z,\) biết: \(\left( {n - 5} \right) \vdots \left( {n{\rm{ }} + 2} \right)\).
\((n - 5) \vdots (n + 2) \Rightarrow [(n + 2) - 7] \vdots (n + 2)\)
Vì \((n + 2) \vdots (n + 2)\) và \(n \in Z\) nên để \((n - 5) \vdots (n + 2)\) thì \(7 \vdots (n + 2)\)
Hay \(n + 2 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)
Ta có bảng:

Vậy \(n \in \left\{ { - 9; - 3; - 1;5} \right\}\).
Có bao nhiêu số nguyên \(a > 3\) biết: \(20\) là bội của \(\left( {3a + 5} \right)\).
Vì \(20\) là bội của \(3a + 5\) nghĩa là \(3a + 5\) là ước của \(20\)
\(U\left( {20} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 5; \pm 10; \pm 20} \right\}\)
Ta có bảng:
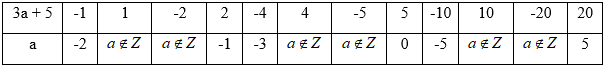
Mà \(a > 3\) nên \(a \in \left\{ 5 \right\}\)
Vậy có \(1\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên biết: \(\left( {x + 3} \right)\left( {y - 4} \right) = - 5?\)
Ta có: \( - 5 = - 1.5 = - 5.1 = 1.( - 5) = 5.( - 1)\)
Ta có bảng:
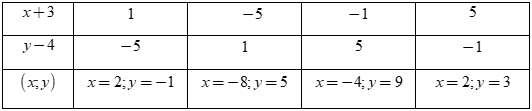
Vậy có \(4\) cặp số \(\left( {x;y} \right)\) thỏa mãn là: \(\left( {2; - 1} \right),\left( { - 8;5} \right),\left( { - 4;9} \right),\left( {2;3} \right)\).
Tìm \(x,\) biết: \(x\, \vdots \,7\) và \(42 \,\vdots \,x\).
Ta có:
\(A = B\left( 7 \right) = \left\{ {0; \pm 7; \pm 14; \pm 21; \pm 28; \pm 35...} \right\}\)
\(B = U\left( {42} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 6; \pm 7; \pm 14; \pm 21; \pm 42} \right\}\)
Vậy \(x \in \left\{ { \pm 7; \pm 14; \pm 21} \right\}\).
Tìm số nguyên \(x\) thỏa mãn \({11^2}.x = {\left( { - 10} \right)^5} + 21x\).
\(\begin{array}{l}{11^2}x = {( - 10)^5} + 21x\\121x = {( - 10)^5} + 21x\\121x - 21x = {( - 10)^5}\\100x = - 100000\\x = - 1000\end{array}\).
Tìm \(a;b \in Z\) thỏa mãn \(312a - 27b = 2002\).
Vì vế trái chia hết cho 3, nhưng vế phải không chia hết cho 3. Nên không tồn tại cặp số nguyên \((a,b)\) thỏa mãn bài toán.
Gọi \(A\) là tập hợp các giá trị \(n \in Z\) để \(\left( {{n^2} + 2} \right)\) là bội của \(\left( {n + 2} \right)\). Số các phần tử của \(A\) là:
Ta có:
\(\begin{array}{l}{n^2} + 2 = {n^2} + 2n - 2n - 4 + 6\\ = n(n + 2) - 2(n + 2) + 6\\ = (n - 2)(n + 2) + 6\end{array}\)
Vì \(n \in Z\) nên để \({n^2} + 2\) là bội của \(n + 2\) thì \(6\) là bội của \(n + 2\) hay \(n + 2\) là ước của \(6\)
\(U\left( 6 \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 6} \right\}\) nên \(n + 2 \in \left\{ { \pm 1; \pm 2; \pm 3; \pm 6} \right\}\)
Ta có bảng:

Vậy \(n \in A = \left\{ { - 8; - 5; - 4; - 3; - 1;0;1;4} \right\}\)
Do đó số các phần tử của \(A\) là \(8\).
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(6x + 11y\) là bội của \(31\) thì \(x + 7y\) là bội của số nào dưới đây?
Ta có:
\(\begin{array}{l}6x + 11y = 6x + 42y - 31y\\ = \left( {6x + 42y} \right) - 31y\\ = 6\left( {x + 7y} \right) - 31y\end{array}\)
Vì \(6x + 11y\) chia hết cho \(31\) và \(31y\) chia hết cho \(31\) nên suy ra \(6\left( {x + 7y} \right)\) chia hết cho \(31\)
Mà \(6\) không chia hết cho \(31\) nên suy ra \(x + 7y\) chia hết cho \(31\)
Vậy nếu \(6x + 11y\) chia hết cho \(31\) thì \(x + 7y\) cũng chia hết cho \(31\)
Hay \(6x + 11y\) là bội của \(31\) thì \(x + 7y\) cũng là bội của \(31\).
Cho $a,b \in Z$ và $b \ne 0.$ Nếu có số nguyên $q$ sao cho $a = bq$ thì
Với $a,b \in Z$ và $b \ne 0.$ Nếu có số nguyên $q$ sao cho $a = bq$ thì \(a\) là bội của \(b\) và \(b\) là ước của \(a\)
Các bội của $6$ là:
Bội của $6$ là số $0$ và những số nguyên có dạng \(6k\,\left( {k \in {Z^*}} \right)\)
Các bội của $6$ là: \(0;\;\,6;\, - 6;\;\,12;\, - 12;\,...\)
Tập hợp các ước của $ - 8$ là:
Ta có: \( - 8 = - 1.8 = 1.\left( { - 8} \right) = - 2.4 = 2.\left( { - 4} \right)\)
Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
Có bao nhiêu số nguyên \(x\) biết: $x\; \vdots \;5$ và $\left| x \right| < 30?$
\(B\left( 5 \right) = \left\{ {0; \pm 5; \pm 10; \pm 15; \pm 20; \pm 25; \pm 30;...} \right\}\)
Vậy các số nguyên \(x\) cần tìm là: \(\left\{ {0; \pm 5; \pm 10; \pm 15; \pm 20; \pm 25} \right\}\)
Có tất cả \(11\) số nguyên cần tìm.
Tính nhanh $\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)$ ta được kết quả là
$\begin{array}{l}\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)\\ = \left[ {125.\left( { - 8} \right)} \right].\left[ {\left( { - 5} \right).20} \right].\left( { - 2} \right)\\ = - \left( {125.8} \right).\left[ { - \left( {5.20} \right)} \right].\left( { - 2} \right)\\ = \left( { - 1000} \right).\left( { - 100} \right).\left( { - 2} \right)\\ = 100000.\left( { - 2} \right) = - 200000\end{array}$
Tìm tất cả các ước chung của $ - 18$ và $30.$
Ta có:
\(Ư\left( {-18} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 6; \pm 9; \pm 18} \right\}\)
$Ư\left( {30} \right)=\left\{ { \pm 1; \pm 2; \pm 3; \pm 5; \pm 6; \pm 10; \pm 15; \pm 30} \right\}$
Vậy ƯC\(\left( { - 18;30} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 6} \right\}\)

