Câu hỏi:
2 năm trước
Có bao nhiêu số nguyên \(a > 3\) biết: \(20\) là bội của \(\left( {3a + 5} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: a
Vì \(20\) là bội của \(3a + 5\) nghĩa là \(3a + 5\) là ước của \(20\)
\(U\left( {20} \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 5; \pm 10; \pm 20} \right\}\)
Ta có bảng:
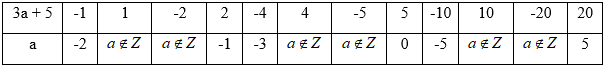
Mà \(a > 3\) nên \(a \in \left\{ 5 \right\}\)
Vậy có \(1\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Hướng dẫn giải:
\(20\) là bội của \(3a + 5\) nghĩa là \(3a + 5\) là ước của \(20\)
- Tìm các ước của \(20\)
- Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận.
Câu hỏi khác
- Bài tập tập hợp các số nguyên môn toán 6 sách KNTT có lời giải
- Bài tập các dạng toán về thứ tự trong tập hợp số nguyên môn toán 6 sách KNTT có lời giải
- Bài tập các dạng toán về tập hợp các số nguyên môn toán 6 sách KNTT có lời giải
- Bài tập thứ tự trong tập hợp số nguyên môn toán 6 sách KNTT có lời giải
- Bài tập phép cộng hai số nguyên môn toán 6 sách KNTT có lời giải
