Một cái cổng hình parabol có dạng \(y = - \dfrac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)
Tính chiều cao \(h\) của cổng (xem hình minh họa)
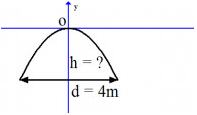
Đáp án: \(h = \)
$m$
Đáp án: \(h = \)
$m$
Bước 1:
Gọi hai điểm chân cổng là \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) thì ta có \({y_A} = {y_B}\) và \(\left| {{x_A}} \right| = \left| {{x_B}} \right|.\)
Vì \(d = 4\) nên \(\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2.\)
Bước 2: Tính $h$
Vậy \(h = \left| {{y_A}} \right| = \left| { - \dfrac{1}{2}x_A^2} \right| = \left| { - \dfrac{1}{2}{{.2}^2}} \right| = 2\,\left( m \right).\)
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn cách điểm bắn \(80\;{\rm{m}}\).
Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?
Bước 1: Đặt hệ trục tọa độ. Gọi \((P):y = a{x^2} + bx + c\). Tìm (P).
Đặt hệ trục như hình vẽ.
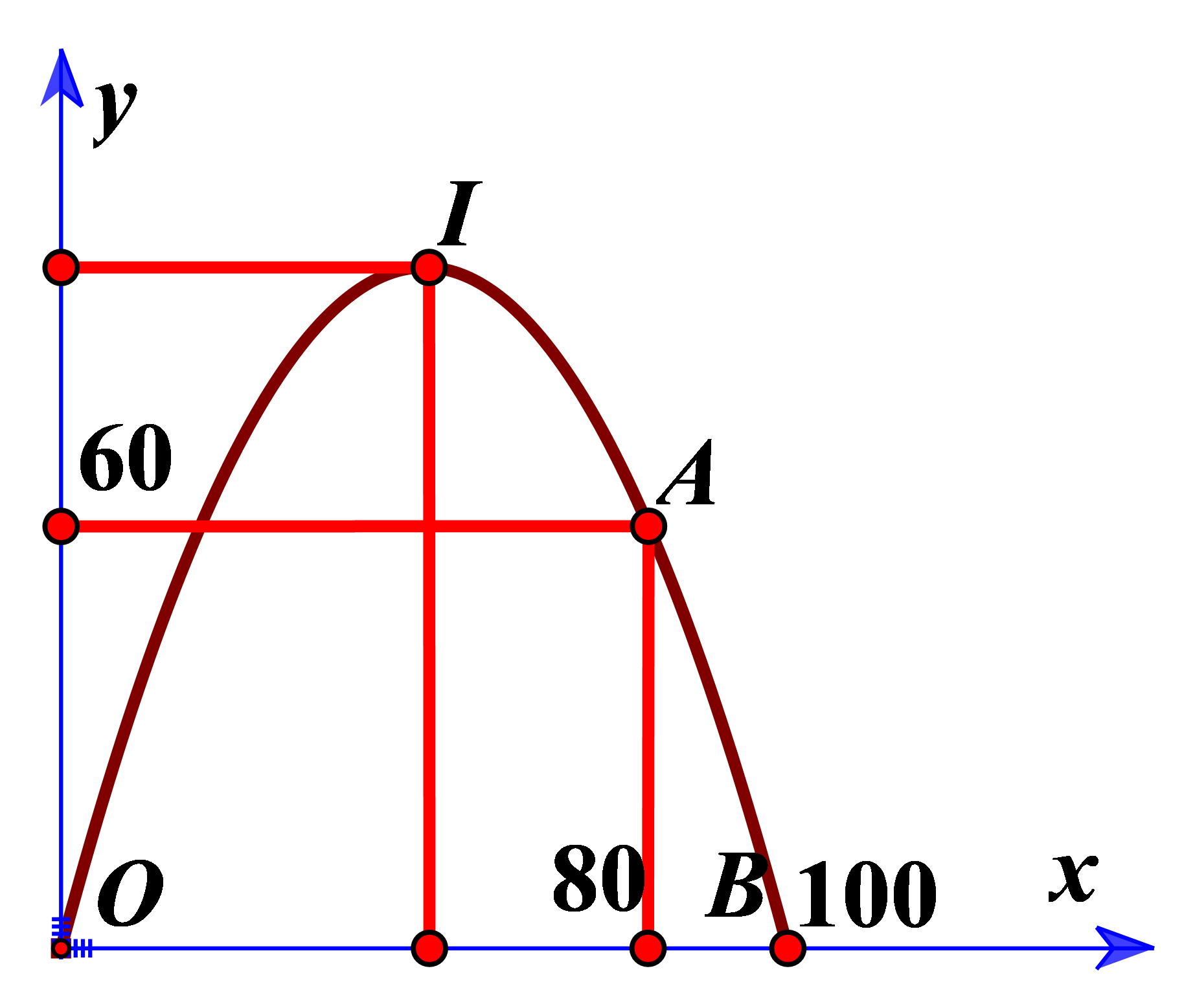
Gọi \((P):y = a{x^2} + bx + c\).
Ta có \((P)\) qua \(O(0;0),A(80;60)\) và \(B(100;0)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0}\\{{{80}^2}a + 80b = 60}\\{{{100}^2}a + 100b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \dfrac{3}{{80}}}\\{b = \dfrac{{15}}{4}}\end{array}} \right.} \right.\)
\( \Rightarrow (P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\)
Bước 2: Tìm đỉnh của (P)
Vị trí đạn bay cao nhất cách mặt đất là \({y_I} = - \dfrac{\Delta }{{4a}} = - \dfrac{{{b^2} - 4ac}}{{4a}} = \dfrac{{375}}{4} = 93,75m\).
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn cách điểm bắn \(80\;{\rm{m}}\).

Máy bắn đá cách tường thành địch \(90\;{\rm{m}}\). Biết tường thành cao \(30\;{\rm{m}}\). Hỏi chiều cao khi đạn bay đến tường thành thì cao hơn hay thấp hơn tường thành bao nhiêu mét?
\((P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\).
Vì máy bắn đá cách tường thành địch 90 m nên \(x = 90 \Rightarrow y = 33,75(m) > 30(m)\)
\( \Rightarrow \) đạn pháo cao hơn tường thành 3,75m
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn cách điểm bắn \(80\;{\rm{m}}\).

Địch xây chòi phòng thủ cao \(20\;{\rm{m}}\) phía trước tường thành. Hỏi phải đặt máy bắn đá cách chòi bao xa để đạn có thể bắn trúng chòi? Biết rằng để tránh bị địch tấn công thì máy bắn đá phải đặt cách thành địch ít nhất \(50\;{\rm{m}}\).
Để máy bắn đá có thể bắn trúng chòi cao \(20\;{\rm{m}}\) thì
\( - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x = 20 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 94,35(m)}\\{x = 5,65(m)(L)}\end{array}} \right.\)
Vậy cần đặt máy bắn đá cách chòi 94,35 m để đạn có thể bắn trúng chòi.
Bảng giá cước của một hãng taxi $\mathrm{X}$ được cho như bảng dưới đây:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
Thiết lập công thức liên hệ giữa quãng đường di chuyển và số tiền tương ứng phải trả. Nếu một người đi taxi của hãng $\mathrm{X}$ phải trả số tiền xe là $475000 \mathrm{VNĐ}$ thì người đó đã đi quãng đường là bao nhiêu?
Bước 1: Lập công thức
$f(x) = $\(\begin{array}{l}\left\{ \begin{array}{l}10000x(0 < x \le 10)\\10000 \cdot 10 + (x - 10) \cdot 15000(10 < x \le 40)\\10000 \cdot 10 + 15000 \cdot 30 + (x - 40) \cdot 12500(x > 40)\end{array} \right.\\ \Leftrightarrow f(x) = \left\{ {\begin{array}{*{20}{c}}{10000x}&{(0 < x \le 10)}\\{15000x - 50000}&{(10 < x \le 40)}\\{12500x + 50000}&{(x > 40)}\end{array}} \right.\end{array}\)
Bước 2: Xác định các khoảng của $f(x)$ ứng với các khoảng của $x$
Để xác định số tiền xe là $475000$VNĐ mà người đi xe phải trả ứng với quãng đường di chuyển dài bao nhiêu, ta cần xác định công thức tương ứng
Với $f(x)=10000 x, 0<x \leq 10$ thì $0<f(x) \leq 100000$
Với $f(x)=15000 x-50000,10<x \leq 40$ thì $100000<f(x) \leq 550000$
Với $f(x)=12500 x+50000, x>40$ thì $f(x)>550000$
Bước 3: Tìm $x$ khi $f(x)=475 000$
Vi $100000<475000<550000$ nên ứng với số tiền xe $475000 \mathrm{VNĐ}$ ta có:
$15000x-50000=475 000$
Người đi xe đã đi được quãng đường là $\dfrac{475000+50000}{15000}=35(\mathrm{~km})$
Vậy người đó đã đi được quãng đường dài $35 \mathrm{~km}$
Bảng giá cước của một hãng taxi $\mathrm{X}$ được cho như bảng dưới đây:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
Một người đi taxi của hãng $\mathrm{X}$ từ $A$ đến $B$, sau đó phải bắt taxi một lần nữa để đi từ $B$ đến $C$. Biết quãng đường $A B$ trong khoảng từ 10 đến $40 \mathrm{~km}$, quãng đường $B C$ dài hơn quãng đường $A B$ là $32 \mathrm{~km}$. Số tiền người đó phải trả ở quãng đường $B C$ gấp 2,8 lần số tiền phải trả ở quãng đường $A B$. Tính độ dài quãng đường $A B$
Bước 1: Gọi $x(k m)(10<x<40)$ là độ dài quãng đường $A B$
Gọi $x(k m)(10<x<40)$ là độ dài quãng đường $A B$.
Vì quãng đường $B C$ dài hơn quãng đường $A B$ là $32 \mathrm{~km}$ nên quãng đường $B C$ dài $x+32(k m)$
Bước 2: Lập phương trình
Vì số tiền người đó phải trả ở quãng đường $B C$ gấp 2,8 lần số tiền phải trả ở quãng đường $A B$ nên ta có phương trình
\(\begin{array}{l}12500(x + 32) + 50000\\ = 2,8 \cdot (15000x - 50000)\\ \Leftrightarrow x = 20(km)\end{array}\)
Vậy quãng đường $A B$ dài $20 \mathrm{~km}$
Bảng giá cước của một hãng taxi $\mathrm{X}$ được cho như bảng dưới đây:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
Ngày Valentine, hãng $X$ áp dụng chương trình giảm giá $10 \%$ cho khách hàng, tối đa $50000$VNĐ. Một người đi taxi của hãng $\mathrm{X}$ trong dịp này phải trả $360000$VNĐ thì người đó đã đi quãng đường là bao nhiêu?
Bước 1: Số tiền chưa được giảm=Số tiền đã trả:(100%-10%)
Nếu không được giảm giá $10 \%$ thì người đi xe phải trả số tiền là:
$360000 :(100 \%-10 \%)=400000$(đồng)
Bước 2: Tìm quãng đường
Vì $100000<400000<550000$ nên người đi xe đã đi được quãng đường là:
$\dfrac{400000+50000}{15000}=30(\mathrm{~km})$
Vậy người đó đã đi được quãng đường dài $30 \mathrm{~km}$

