Trong không gian Oxyz , cho đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y - 4}}{1} = \dfrac{{z - 2}}{1}\) và 2 điểm \(A\left( {6;3; - 2} \right)\); \(B\left( {1;0; - 1} \right)\). Gọi \(\Delta \) là đường thẳng đi qua \(B\), vuông góc với \(d\) và thỏa mãn khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất. Một vectơ chỉ phương của \(\Delta \) có tọa độ :
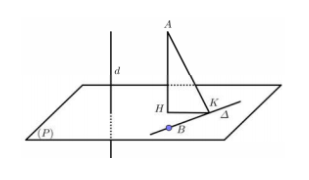
Gọi \(\left( P \right)\) là mặt phẳng đi qua \(B\) và vuông góc với \(d \Rightarrow \left( P \right):\,\,2x + y + z - 1 = 0\).
\(\Delta \) đi qua \(B\) và vuông góc với \(d \Rightarrow \Delta \subset \left( P \right)\).
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(\Delta \) ta có \(AH \le AK\).
Do đó để khoảng cách từ \(A\) đến \(\Delta \) là nhỏ nhất \( \Rightarrow H \in \Delta \).
Phương trình \(AH\) đi qua \(A\) và nhận \(\overrightarrow {{u_d}} = \left( {2;1;1} \right)\) là 1 VTCP là \(\left\{ \begin{array}{l}x = 6 + 2t\\y = 3 + t\\z = - 2 + t\end{array} \right.\).
\(\begin{array}{l}H \in AH \Rightarrow H\left( {6 + 2t;3 + t; - 2 + t} \right)\\H \in \left( P \right) \Rightarrow 2\left( {6 + 2t} \right) + 3 + t - 2 + t - 1 = 0 \Leftrightarrow 6t + 12 = 0 \Leftrightarrow t = - 2\\ \Rightarrow H\left( {2;1; - 4} \right)\end{array}\)
\(\Delta \) đi qua \(B,\,\,H\) nhận \(\overrightarrow {BH} \left( {1;1; - 3} \right)\) là 1 VTCP.
Trong không gian \(Oxyz\) cho điểm \(A\left( {1;1; - 2} \right)\) và đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{1} = \dfrac{z}{{ - 2}}\). Đường thẳng qua A và song song với d có phương trình tham số là
Đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{1} = \dfrac{z}{{ - 2}}\) có 1 VTCP là \(\overrightarrow {{u_d}} = \left( {2;1; - 2} \right)\), đây cũng là VTCP của đường thẳng đi qua A và song song với d.
Đường thẳng qua A và song song với d nhận \(\overrightarrow u = \left( {2;1; - 2} \right)\) là VTCP, có phương trình tham số: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + t\\z = - 2 - 2t\end{array} \right.\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 - 3t\end{array} \right.\). Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O\), vuông góc với trục hoành \(Ox\) và vuông góc với đường thẳng \(d\) có phương trình là:
Đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 - 3t\end{array} \right.\) có 1 VTCP là \(\overrightarrow {{u_d}} = \left( {1; - 1; - 3} \right)\), trục \(Ox\) có 1 VTCP là \(\overrightarrow i = \left( {1;0;0} \right)\).
Gọi \(\overrightarrow {{u_\Delta }} \) là 1 VTCP của đường thẳng \(\Delta \), ta có \(\left\{ \begin{array}{l}\Delta \bot Ox\\\Delta \bot d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} .\overrightarrow i = 0\\\overrightarrow {{u_\Delta }} .\overrightarrow {{u_d}} = 0\end{array} \right. \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow i ;\overrightarrow {{u_d}} } \right] = \left( {0; - 3;1} \right)\).
Vậy phương trình đường thẳng \(\Delta \) đi qua \(O\left( {0;0;0} \right)\) và có 1 VTCP \(\overrightarrow {{u_\Delta }} = \left( {0; - 3;1} \right)\) là: \(\Delta :\,\,\left\{ \begin{array}{l}x = 0\\y = - 3t\\z = t\end{array} \right.\).
Trong không gian Oxyz, đường thẳng \(d:\dfrac{{x + 2}}{1} = \dfrac{{y - 3}}{2} = \dfrac{{z - 11}}{{ - 1}}\) và hai điểm $A(1;2;4)$, $B(0;0;m)$ cùng nằm trong một mặt phẳng khi $m$ bằng:
Bước 1: Xác định điểm M và VTCP của d.
Xét d có \(M\left( { - 2;2;11} \right) \in d\) và \(\overrightarrow u \left( {1;2; - 1} \right)\) là vecto chỉ phương của d.
Ta có:
\(\overrightarrow {AM} \left( { - 3;1;7} \right);\overrightarrow {AB} \left( { - 1; - 2;m - 4} \right)\)
Bước 2:
Đường thẳng d, A, B đồng phẳng <=> \(\overrightarrow u ,\overrightarrow {AB} ,\overrightarrow {AM} \) đồng phẳng.
<=> \(\left[ {\overrightarrow u ,\overrightarrow {AM} } \right].\overrightarrow {AB} = 0\)
Bước 3:
Xét \(\left[ {\overrightarrow u ,\overrightarrow {AM} } \right].\overrightarrow {AB} \)
\(\begin{array}{l} = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&7\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&1\\7&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&2\\{ - 3}&1\end{array}} \right|} \right).\overrightarrow {AB} \\ = \left( {15; - 4;7} \right).\left( { - 1; - 2;m - 4} \right)\end{array}\)
\( = - 15 + 8 + 7m - 28 = 7m - 35\)
\(\left[ {\overrightarrow u ,\overrightarrow {AM} } \right].\overrightarrow {AB} = 0 \Leftrightarrow 7m - 35 = 0\)\( \Leftrightarrow m = 5\)

