Mặt cầu và đường thẳng

Dễ thấy \(E \in \left( P \right)\) . Gọi I\(\left( {3;2;5} \right)\) là tâm khối cầu.

Đường thẳng qua I vuông góc với (P): \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 2 + 2t\\z = 5 - t\end{array} \right.\,\,\left( d \right)\).

Gọi H là hình chiếu của I lên (P) \( \Rightarrow H \in \left( d \right) \Rightarrow H\left( {3 + 2t;2 + 2t;5 - t} \right)\)

Lại có \(H \in \left( P \right)\)

\(\begin{array}{l} \Rightarrow 2\left( {3 + 2t} \right) + 2\left( {2 + 2t} \right) - 5 + t - 3 = 0\\ \Leftrightarrow 6 + 4t + 4 + 4t - 5 + t - 3 = 0\\ \Leftrightarrow 9t + 2 = 0 \Leftrightarrow t = \dfrac{{ - 2}}{9} \Rightarrow H\left( {\dfrac{{23}}{9};\dfrac{{14}}{9};\dfrac{{47}}{9}} \right)\\ \Rightarrow \overrightarrow {EH} \left( {\dfrac{5}{9};\dfrac{5}{9};\dfrac{{20}}{9}} \right) = \dfrac{5}{9}\left( {1;\;1;\;4} \right)//\left( {1;1;4} \right) = \overrightarrow a \end{array}\)

Để đường thẳng \(\left( \Delta  \right)\) cắt mặt cầu (S) tại 2 điểm sao cho chúng có khoảng cách nhỏ nhất thì đường thẳng \(\left( \Delta  \right)\) đi qua E và vuông góc với \(HE\).

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{u_\Delta }}  \bot \overrightarrow {{n_P}} \\\overrightarrow {{u_\Delta }}  \bot \overrightarrow a \end{array} \right. \Rightarrow \overrightarrow {{u_\Delta }}  = \left[ {\overrightarrow {{n_P}} ;\overrightarrow a } \right] = \left( {\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l} - 1\\4\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l} - 1\\4\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|} \right) = \left( {9; - 9;\;0} \right) = 9\left( {1; - 1;0} \right)\).

Vậy đường thẳng \(\left( \Delta  \right)\) đi qua E và nhận \(\left( {1; - 1;0} \right)\) là 1 VTCP.

Vậy phương trình đường thẳng \(\left( \Delta  \right):\,\,\left\{ \begin{array}{l}x = 2 + t\\y = 1 - t\\z = 3\end{array} \right.\)

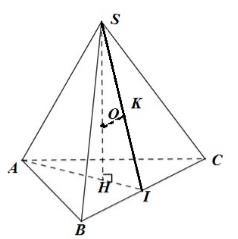
Xét tứ diện SABC có: \(SA = SB = SC\), \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0}\)\( \Rightarrow SABC\) là tứ diện đều.

Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\) có tâm O, bán kính \(R = 3\), ngoại tiếp khối tứ diện SABC \( \Rightarrow OS = OA = OB = OC = 3\)

Giả sử độ dài dây AB là  a  \( \Rightarrow \,SI = AI = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow \,AH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)

\( \Rightarrow SH = \sqrt {S{A^2} - A{H^2}}  = \sqrt {{a^2} - \dfrac{1}{3}{a^2}}  = \sqrt {\dfrac{2}{3}} a\)

\( \Rightarrow R = \dfrac{{{a^2}}}{{2\sqrt {\dfrac{2}{3}} a}} = \dfrac{{\sqrt 6 a}}{4} \Rightarrow \dfrac{{\sqrt 6 a}}{4} = 3 \Leftrightarrow a = 2\sqrt 6 \).

Khoảng cách từ tâm \(I\) đến trục \(Oz\) là: \(d\left( {I;\left( {Oz} \right)} \right) = \sqrt {{3^2} + {4^2}}  = 5.\)

Vì  tiếp xúc với trục Oz nên bán kính mặt cầu R=5.

Vậy phương trình cần tìm là 

\(\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 25.\)

Bước 1: Biểu diễn M và vectơ chỉ phương của \(\Delta \) theo m.

Mặt phẳng \((\alpha ):x - my + z + 6m - 3z = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}}  = (1; - m;1)\), và mặt phẳng \((\beta ):mx + y - mz + 3m - 8 = (\alpha ) \cap (\beta )\). \(\overrightarrow {{n_1}}  = (1; - m;1)\), và mặt phẳng \((\beta ):mx + y - mz\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}}  = (m;1; - m).\) Ta có \(M\left( { - 3m + \dfrac{4}{m} - 3;0; - 3m - \dfrac{4}{m}} \right) \in \Delta  = \left( \alpha  \right) \cap \left( \beta  \right)\)

Do đó \(\Delta \) có một vectơ chỉ phương là \(\vec u = \left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {{m^2} - 1;2m;{m^2} + 1} \right)\).

Bước 2: Gọi \((P)\) là mặt phẳng chứa đường thẳng \(\Delta \) và vuông góc với mặt phẳng \((Oxy)\). Tìm c.

Gọi \((P)\) là mặt phẳng chứa đường thẳng \(\Delta \) và vuông góc với mặt phẳng \((Oxy)\). Khi đó \((P)\) có một vectơ pháp tuyến là \(\vec n = [\vec u;\vec k] = \left( {2m;1 - {m^2};0} \right)\).

Phương trình mặt phẳng \((P)\) là : \(2mx + \left( {1 - {m^2}} \right)y + 6{m^2} + 6m - 8 = 0\).

Vì \(I(a;b;c) \in (Oxy)\) nên \(I(a;b;0)\).

Bước 3: Theo giả thiết ta suy ra \((P)\) là tiếp diện của mặt cầu \((S) \Rightarrow d(I;(P)) = R\). Tìm a và b

Theo giả thiết ta suy ra \((P)\) là tiếp diện của mặt cầu \((S) \Rightarrow d(I;(P)) = R\)

\( \Leftrightarrow \dfrac{{\left| {2ma + \left( {1 - {m^2}} \right)b + 6{m^2} + 6m - 8} \right|}}{{\sqrt {4{m^2} + {{\left( {1 - {m^2}} \right)}^2}} }} = R > 0\)

\( \Leftrightarrow \dfrac{{\left| {2m(a + 3) + (6 - b){m^2} + b - 8} \right|}}{{{m^2} + 1}} = R > 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2m(a + 3) + (6 - b){m^2} + b - 8 = R\left( {{m^2} + 1} \right)}\\{2m(a + 3) + (6 - b){m^2} + b - 8 =  - R\left( {{m^2} + 1} \right)}\end{array}} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{2(a + 3) = 0}\\{6 - b = R}\\{b - 8 = R}\\{R > 0}\end{array}} \right.\\\left\{ \begin{array}{l}2(a + 3) = 0\\6 - b =  - R\\b - 8 =  - R\\R > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{a =  - 3 = 0}\\{6 - b = b - 8}\\{ - R = 6 - b < 0}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{a =  - 3}\\{6 - b = b - 8}\\{R = 6 - b > 0}\end{array}} \right.\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}a =  - 3\\b = 7\end{array} \right.\)

Vậy \(I( - 3;7;0)\), do đó \(P = 10{a^2} - {b^2} + 3{c^2} = 41\).