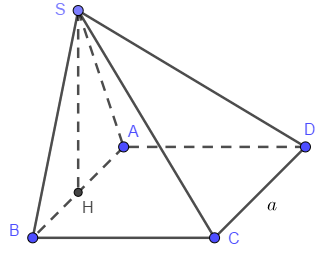
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm H của cạnh AB. Biết tam giác SAB là tam giác đều. Số đo của góc giữa SA và CD là
Bước 1:
\(CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)}\)\( = \widehat {\left( {SA,AB} \right)} = \widehat {SAB}\)
Bước 2:
Vì tam giác SAB là tam giác đều.
\( \Rightarrow \widehat {SAB} = 60^\circ \)
Vậy góc giữa SA và CD là \({60^0}\)
Cho tứ diện $A B C D$ có $A B$ vuông góc với mặt phẳng $(B C D)$. Biết tam giác $B C D$ vuông tại $C$ và các cạnh $A B=\dfrac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a$. Gọi $E$ là trung điểm của $A C$. Góc giữa hai đường thẳng $A B$ và $D E$ bằng
$60^{\circ}$
$60^{\circ}$
$60^{\circ}$
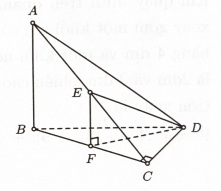
Bước 1: Gọi $F$ là trung điểm của $B C$. Xác định góc giữa AB và DE
Gọi $F$ là trung điểm của $B C$
Xét $\Delta A B C$ có $E ; F$ lần lượt là trung điểm của $A C ; B C$
$\Rightarrow E F$ là đường trung bình của $\Delta A B C$
$\Rightarrow E F / / A B \Rightarrow(\widehat{A B, D E})=(\widehat{E F, D E})$
Ta có $A B \perp(B C D) \Rightarrow E F \perp(B C D) \Rightarrow E F \perp F D$
(vì $F D \subset(B C D)$ )
$\Rightarrow \Delta E F D$ vuông tại $F$ do đó $(\widehat{E F, D E})=\widehat{F E D}$
Bước 2: Tính góc $FED$ và kết luận.
Lại có $\left\{\begin{array}{l}C D \perp B C \\ C D \perp A B\end{array} \Rightarrow C D \perp(A B C) \Rightarrow C D \perp A C\right.$ hay $\Delta A C D$ vuông tại $C$
Xét tam giác vuông $E C D$ có
$E D=\sqrt{E C^{2}+C D^{2}}=\sqrt{\left(\dfrac{A C}{2}\right)^{2}+C D^{2}}=\sqrt{\left(\dfrac{a \sqrt{2}}{2}\right)^{2}+a^{2}}=\dfrac{a \sqrt{6}}{2} .$
Xét $\Delta E F D$ vuông có $\cos \widehat{F E D}=\dfrac{E F}{E D}=\dfrac{A B}{2 E D}=\dfrac{1}{2} \Rightarrow \widehat{F E D}=60^{\circ}$
Vậy góc giữa hai đường thẳng $A B$ và $D E$ bằng $60^{\circ}$

